金屬機身飛機框間距及截面參數分析

馬駿

(上海飛機設計研究院 飛機結構強度工程技術所, 上海 201210)

0 引 言

隔框的間距對機身受壓蒙皮壁板的設計有非常大的影響。同時隔框的間距對壁板的重量也有較大影響，隨著隔框間距的增大，固定在隔框上的地板梁的跨度也會增大，必然導致地板結構重量的變化。

目前國內外資料基本沒有對于框距初步確定的設計分析，都是以經驗值20 in[1]作為說明，Hans-Jürgen Schmidt[2]研究了典型金屬隔框的設計原則并分析了隔框截面形式的選擇；鄧揚晨等[3-4]研究了軍用飛機加強框的拓撲優化設計以及小型飛機普通隔框的設計優化方法；陳振興等[5]研究了民用飛機隔框與蒙皮壁板的連接結構；姜曉偉[6]研究了隔框的逆向設計和數字化加工。但以上研究都偏向于研究單一隔框，并未對隔框間距做過多分析。

本文從穩定性、強度、重量三方面分析框距初步設計值的確定方法，同時對飛機普通隔框的截面形式進行結構參數分析，以期為后期的詳細設計階段提供參考。

1 框間距初步設計分析

1.1 結構穩定性約束

對于飛機機身結構，機身隔框的間距需要保證在設計載荷下，隔框間的壁板不發生失穩。一般民用飛機的機身中間等直段為橫截面近似圓形的薄壁加筋結構。在分析圓柱筒殼的彈性穩定問題時，可以取單位周長的一條殼壁，將其看作是兩端受軸向壓力作用而沿長度支承在彈性基體上的細長板條，當壓力增大到一定數值時，此板條在直線形態下平衡，就喪失了穩定性，而可能在波紋狀的微彎狀態下維持平衡。因此可以選取一段單位周長壁板作為分析模型，如圖1所示。

上述模型的穩定問題可以利用歐拉公式(式(1))進行計算分析。

(1)

Iz為所取模型截面慣性矩，其計算過程如下所示。

首先，計算形心位置，得到中性軸位置。

yc

(2)

A2=l·t2

(3)

A1=h1·t1+2(b1-t1)t1

(4)

A=A1+A2

(5)

(6)

(7)

然后，計算截面慣性矩

Iz=Iz1+Iz2+Iz3+Iz4

(8)

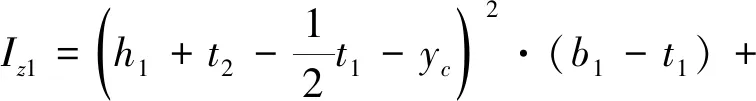
(9)

(10)

(11)

(12)

將以上各式代入歐拉公式，有

(13)

計算采用Lskin=10 m等直段機身簡化模型，不考慮窗框等開口以及地板等部件的影響，參考150座級飛機數據，設計h1=28 mm，蒙皮厚度根據氣密壓差計算(設計載荷下，考慮急速氣動引起的壓差變化以及安全系數，取2倍壓差載荷)，根據計算分析，本文取蒙皮厚度t2=1.2 mm，取飛機極限彎矩M=6.5×109N·mm，機身半徑R=2 000 mm。長桁數量設為86根，計算模型的簡化蒙皮段長度l=145 mm，各部件材料為2024-T3鋁合金。代入式(13)，得到含有框距的一個約束函數。

(14)

1.2 結構強度約束

在強度方面，在機身最上端，彎曲正應力最大，因此根據強度條件有

(15)

式中：[σ]=271.94 MPa

代入數據得到t1和b1的約束函數：

28t1+2(b1-t1)t1>97.90

(16)

1.3 質量計算

飛機結構設計以重量最輕為目標，因此隔框間距以及長桁截面參數的確定要在滿足約束函數的情況下，使得結構重量最輕。

機身質量計算如下：

M=Mskin+Mstringer+Mframe

(17)

Mskin=2πR·Lskin·ρ=0.35 t

(18)

Mstringer=nstringer·A1·Lskin·ρ

(19)

(20)

式中：Aframe為隔框的橫截面積。

Aframe的變化并不影響本節所分析的內容，因此，根據某型民用飛機將Aframe設為定值，令Aframe=220 mm2，由此得到

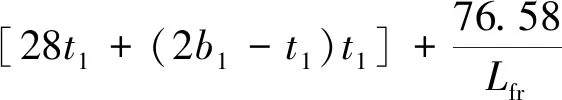
(21)

1.4 結果分析

根據式(14)、式(16)、式(21)繪制隔框間距與機身段重量的關系圖，如圖2所示，可以看出：機身段與隔框間距呈現一定的關系，左側為以拉伸強度為約束條件的曲線，此時由于拉伸靜強度的限制，面積A最小值不會有變化，則蒙皮加筋板的重量不會變化，圖中的重量變化是由于隔框間距增大，導致隔框數量減少從而引起整體重量的降低；隔框間距繼續增大后，約束條件轉變為失穩條件，此處長桁的翻邊寬度，長桁厚度，隔框間距均在變化，綜合作用導致重量的變化。在約束條件切換的地方出現機身重量的最小值，因此，在這個地方附近取設計值接近最優設計值，其設計參數為Lfr=516 mm。

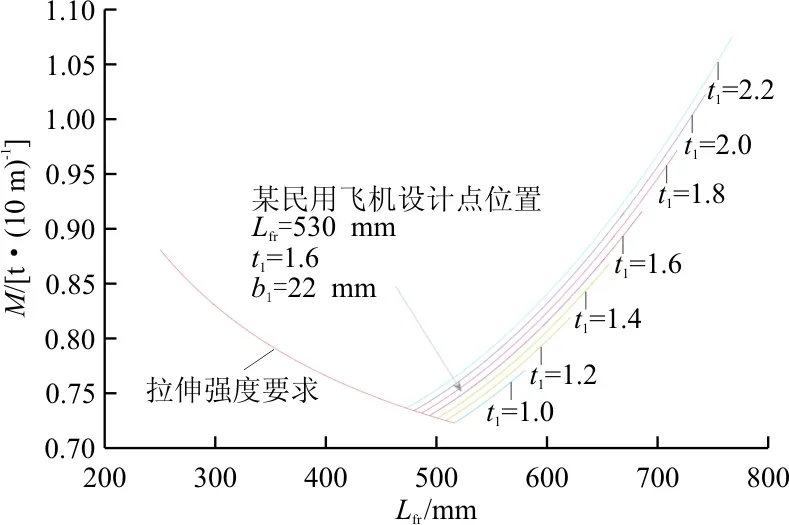
圖2 機身段質量與隔框關系圖

圖2是經過合理簡化得出的，沒有考慮地板組件對失穩的有利影響，因此根據圖2得到的設計點是偏于保守的設計點。上述設計點可以作為初始設計點，在綜合考慮其他各方面因素以及機身結構的具體情況進行調整，例如：內部各種設備的安裝，維護維修的開口，系統管路的要求等。

一般150座級飛機設計經驗值為20 in (508 mm)，與本文分析計算值相符。對于其他構型尺寸的飛機，初始設計值應根據具體情況具體對待，仍可按照本文的設計方法定出初始設計值。

2 隔框結構尺寸分析

座艙普通框和加強框在機身的徑向對座艙殼體的膨脹有很大的約束作用。普通框的主要作用是保持機身的外形，防止蒙皮壁板在縱向壓縮載荷作用下發生彈性失穩[7]。

2.1 隔框尺寸初步分析

上文分析了隔框的間距使得機身筒體不發生框間的局部失穩，即使如此，機身筒體仍有可能發生跨框的總體失穩，普通框的結構剖面尺寸主要取決于框的結構剛度不會引起機身的總體失穩，即最小機身框面內彎曲剛度要求。為了防止機身殼體在承受彎曲時出現總體失穩，所需要的隔框剛度為

(22)

通過對已有試驗數據的研究發現Cf的值為1/16 000[4]，則有

(23)

代入數據計算，得

If≥1.74×105mm4

(24)

為了方便分析，本文分析簡化的隔框直接與蒙皮壁板相連的結構形式，不討論“浮框式”結構，普通隔框示意圖如圖3所示。

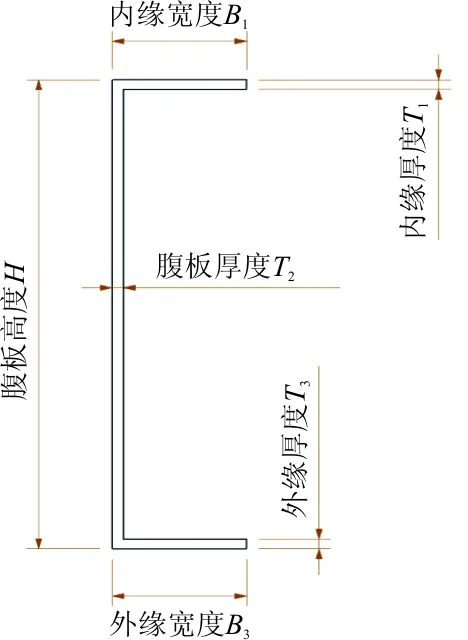
圖3 隔框截面示意圖

計算可得

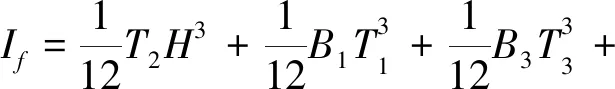
(25)

Af=H·T2+(B1-T2)·T1+(B3-T2)·T3

(26)

對于隔框截面來說，從獲得高截面慣性矩的角度，腹板應該越薄越高，緣條應越厚越短，但是腹板太薄以及緣條寬度太小容易造成側向失穩，同時腹板太高會造成內部空間的減少，這會極大地降低乘坐空間舒適性。

初步設計時，假定T1=T2=T3=1.6 mm，且令B1=B3，由此得到：

If=0.133H3+0.683B1+3.2(0.5H-0.8)2×
(B1-1.6)

(27)

將式(27)代入式(24)得到一個可行域，如圖4所示。

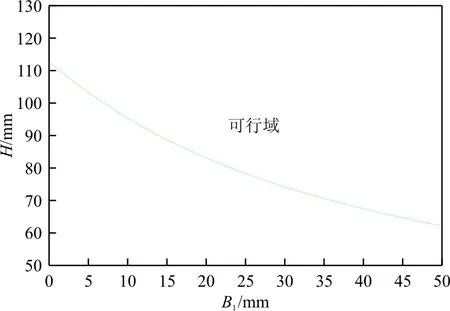
圖4 隔框參數可行域

在可行域內邊界選取若干組合數據，計算截面面積Af以及側向彎曲截面系數Iy，如圖5所示。

圖5 隔框腹板高度影響曲線

在確定隔框截面初步參數時，根據以上分析，參數選取應該使Af盡量小從而重量小，且Iy又不能太小以防止側向失穩，可初步確定H=80～95 mm，從而B1=B3=15 mm。

2.2 格框尺寸參數DOE分析

上文分析了150座級民用飛機隔框間距取值的初步分析方法以及機身普通隔框截面尺寸值初步確定方法。本節通過有限元分析機身普通隔框各個參數對隔框約束條件的重要性，進一步確定隔框的截面參數。使用Isight[8-9]試驗設計(Design of Experiment，簡稱DOE)模塊進行設計分析，自動循環計算隔框結構各尺寸因子對約束的影響。計算模型選取長10 m，半徑2 m的等直段筒段模型，載荷工況為2倍氣密載荷的極限工況，約束條件為蒙皮壁板應力水平。以隔框內緣條厚度、內緣條寬度、外緣條厚度、外緣條寬度、腹板厚度以及腹板寬度6個參數作為變量因子，如表1所示。

表1 參數提取匯總表

對Isight的DOE模塊進行相應設置，采用最優拉丁超立方設計方法進行DOE分析計算，計算結果如圖6所示。圖中顏色表示變量因子與目標約束呈負相關的關系，隔框各項參數的增大皆會導致蒙皮應力的降低。定量分析各參數對蒙皮應力S的相對影響，如表2所示。

圖6 DOE分析結果示意圖

參 數對S的相對系數隔框內緣條厚度-0.17隔框外緣條厚度-0.06隔框腹板厚度-0.88隔框高度-0.40隔框內緣條厚度-0.15隔框外緣條厚度-0.17

從圖6和表2可以看出：隔框腹板厚度對蒙皮應力的影響最大，其次是隔框高度，隔框內緣條寬度影響最小。由此可得，在2倍氣密設計載荷工況下，隔框腹板的厚度對蒙皮應力的影響占主導地位。但是腹板厚度的增加容易造成隔框整體重量的增加，而隔框抗彎截面系數對于腹板厚度值并不敏感，因此一般通過調整隔框的高度，隔框高度對蒙皮應力水平影響較大，同時隔框高度對隔框抗彎截面系數影響也較大。另外DOE分析結果顯示隔框外緣條寬度的影響大于內緣條寬度，且外緣條還需要與蒙皮壁板進行連接，因此設計時隔框外緣條寬度應大于內緣條寬度。

DOE分析結果可為后期詳細設計優化階段作參考，影響大的參數作為優化變量，影響小的參數選取常量，以節省優化資源[10]。

3 結 論

(1) 提出了一種簡化計算模型，即選取蒙皮壁板單位周長壁板截面，以靜強度和局部穩定性為約束條件，計算出隔框間距初步設計值，并與現有民用飛機隔框間距設計經驗值20 in(508 mm)比較，結果吻合很好。

(2) 分析了普通隔框截面參數初步設計方法，對150座級飛機給出了隔框截面參數可行域，初步確定H=80～95 mm，從而B1=B3=15 mm。

(3) 分析了隔框各個參數對于蒙皮應力的影響大小，初步確定隔框外緣條寬度的影響大于內緣條寬度，且外緣條還需要與蒙皮壁板進行連接，因此設計時隔框外緣條寬度應大于內緣條寬度。