一種用于輸電線路的非線性二節點直線索單元

何光遠，朱文滔

（1.廣東南海電力設計院工程有限公司，廣東 佛山 528200；2.廣東電網有限責任公司佛山供電局，廣東 佛山 528200）

0 引 言

目前，架空線路設計中，導地線張力和弧垂計算主要通過微分方程分析微元段受力，并推導相應的懸鏈線方程[1]。為方便工程應用，一般均簡化為拋物線方程。這些方法在以下三種情況下存在明顯局限性。（1）對于風速較高工況的張力和弧垂計算，導地線存在豎向自重弧垂和水平弧垂，采用無風或低風速的拋物線狀態方程式誤差較大；若采用精確的懸鏈線方程，則計算復雜，需迭代求解，存在不收斂情況。（2）對于檔距內存在多個集中荷載或不同均布荷載的情況，需推導不同公式；連續檔更加復雜，需假設懸垂串偏移量進行迭代求解，存在不收斂情況，通用性差。（3）目前，架空線路設計時，分開計算鐵塔和導地線；但實際上，塔線是一體的，采用有限元計算顯然無法滿足塔線一體化設計要求。因此，本文根據架空線路設計特點，提出了二節點直線索單元。

1 位移函數

設桿單元沿弦長方向任意1點3個方向的位移uv、w均為x的函數，且則有：

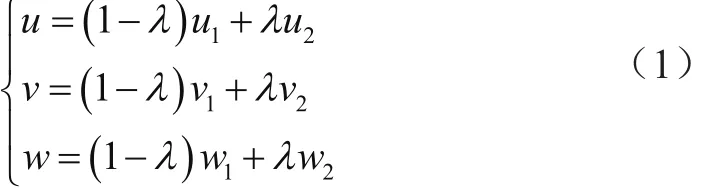
2 非線性幾何方程

取變形前桿上一微元段PA，長度為dx，忽略高階微量，則增量形式的應變位移關系可表示為：

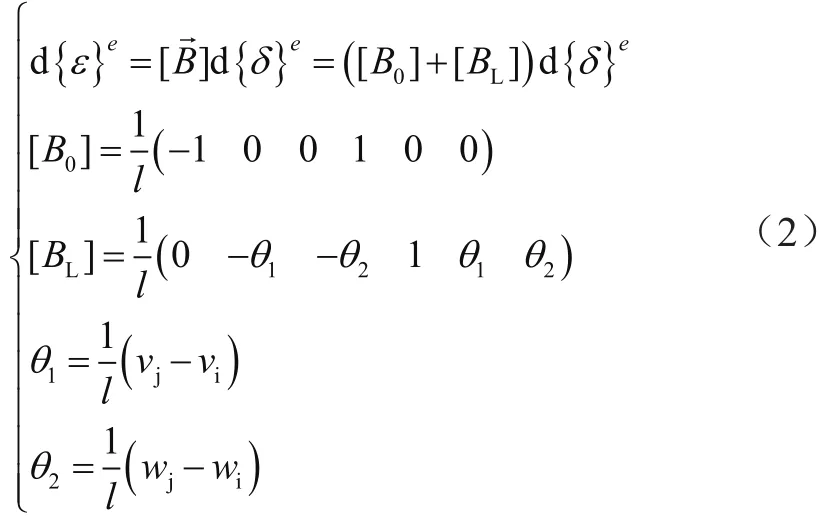
3 物理方程

對于導地線，需考慮初張力和溫差的影響，根據胡克定律可得：

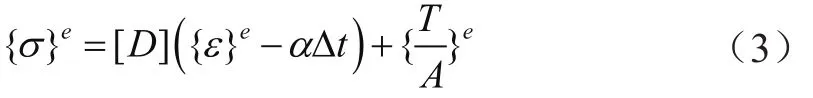
其中，[D]為材料的本構關系矩陣，α為導地線溫度膨脹系數，Δt為當前狀態相對初始狀態的溫差，T為初始狀態導地線的初張力，A為導地線截面積。

4 切線剛度矩陣

由虛功方程可建立單元應力與外力的關系，為保證幾何非線性分析時剛度矩陣對稱，可寫成增量形式：

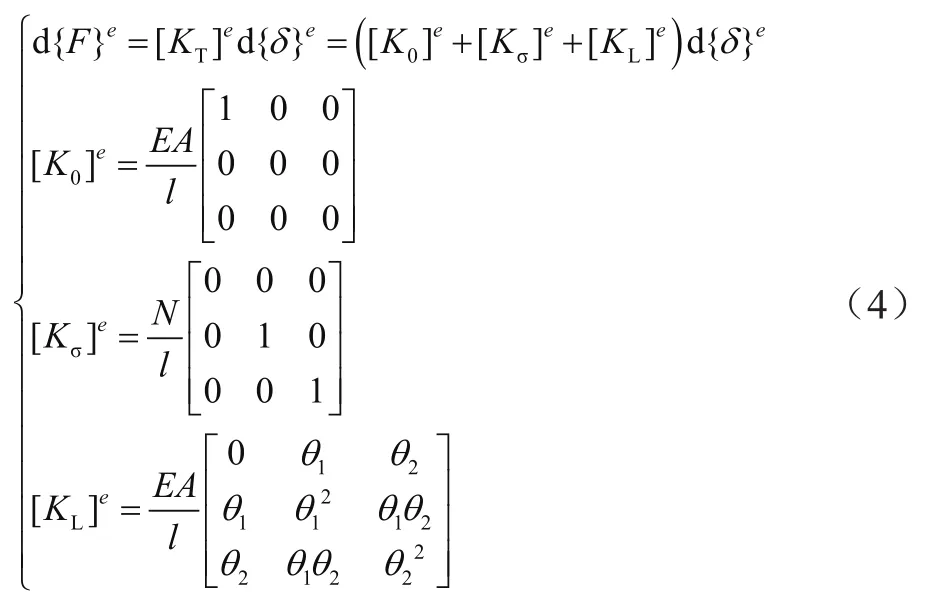
其中，[KT]e為單元切線剛度矩陣，由一般線性分析時的單元剛度矩陣[K0]e、單元初應力矩陣[Kσ]e及單元大位移矩陣[KL]e組成，N由式（3）乘以導地線截面積A計算得出，E為導地線彈性模量。對于導地線，線性分析時無橫向剛度，結構屬于可變體系，無法計算[2]，但非線性分析時，橫向剛度可由初應力矩陣提供，保證結構正常計算。

5 坐標轉換矩陣

對于導地線計算，局部坐標系與整體坐標系各參數相互轉化時無需考慮導地線風偏平面的影響，則轉換矩陣為：

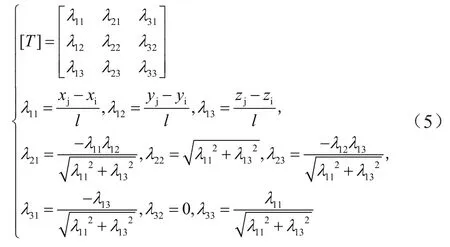
6 荷載等效

工程計算中，導地線所受荷載主要有自重荷載和風荷載，有限元計算時需等效成節點荷載，可表示為：

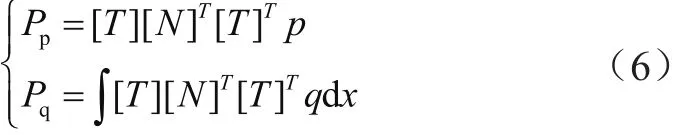
其中，p和q為整體坐標系下單元的集中荷載和均布荷載，pp和pq為等效后的整體坐標系下節點的集中荷載和均布荷載。

7 初始找形

非線性分析前需確定導地線初始平衡線形，取只有自重荷載，無風荷載，溫度為0 ℃時的工況為初始線形，其余工況在此基礎上進行疊加計算。設導地線兩端懸掛點坐標為(x1,y1,z1)和(x2,y2,z2)，則局部坐標系下導地線各點坐標為：

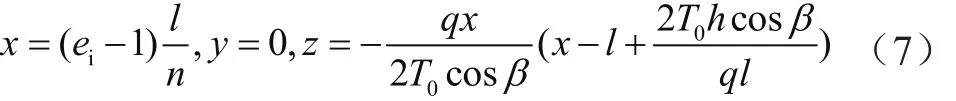
整體坐標系下導地線各點坐標可按式（5）換算，但應注意采用懸掛點坐標。

8 算例分析

圖1為算例1的計算模型圖，懸索跨度為16 m，水平張力H=85.15kN，集中荷載間距為4 m，初始狀態的荷載值分別為P1=P2=P3=16kN，最大垂度為f=1.503 m，懸索的截面積A=10 cm2，彈性模量E=18 000kN/cm2。當荷載改變為P1=P2=20kN，P3=16kN時，計算各荷載作用點的垂度和各索段的張力，結果如表1所示。其中，與理論值誤差分別為0.15%、0.28%、0.12%、0.30%、0.32%、0.34%、0.36%。

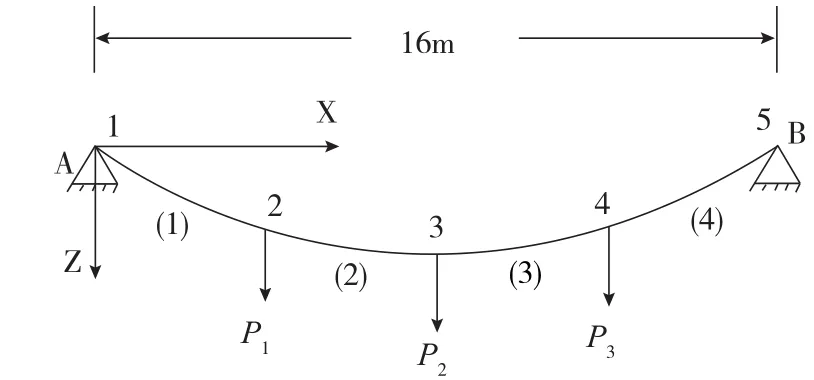
圖1 算例1計算模型

各荷載作用點的位移迭代曲線和各索段的張力迭代曲線分別如圖2和圖3所示。

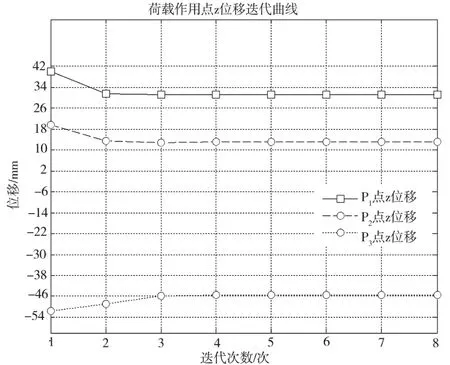
圖2 位移迭代曲線圖

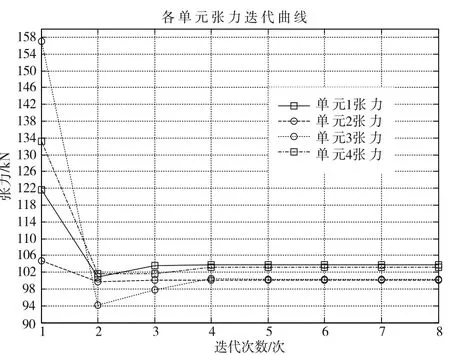
圖3 張力迭代曲線圖

算例2，某110kV線路，導線型號為LGJ-300/40，檔距為300 m，懸掛點無高差，已知風速v=0 m/s，溫度t=15 ℃時跨中弧垂為5.714 m，水平張力為21.9kN，計算最高氣溫（v=0 m/s，t=40 ℃）、最大風速（v=30 m/s，t=10 ℃）、安裝（v=10 m/s，t=5 ℃）、年平均溫（v=0 m/s，t=15 ℃）及導線發熱（v=0 m/s，t=70 ℃）工況下的綜合弧垂和水平張力，結果如表2所示。

表2 算例2計算結果

9 結 論

本文提出的直線索單元精度較好，可模擬導地線在自重荷載、風荷載和集中荷載作用下的變形和受力，可滿足輸電線路導地線的各種復雜設計計算。雖然直線索單元的精度比兩節點和多節點索單元的精度低，但計算簡化極大，避免了不同風偏平面或者同一風偏平面不同單元轉換矩陣不一致的問題，提高了通用性。此外，本文采用的通用有限元的推導方法，可與現有鐵塔計算的梁桿單元無縫對接，為拉線塔及塔線一體的非線性計算提供可行的理論依據。導地線計算時，對于低風速情況（0＜v≤20 m/s），可直接按式（7）給定初始節點坐標計算，即可收斂；對于高風速情況（v＞20 m/s），式（7）中的y坐標可按5 m/s風速確定，即可收斂。