定位方案三維穩健性分析及一般解推導

林 嘉, 楊夫勇, 鄭 丞, 金 隼

(1. 上海交通大學 上海市復雜薄板結構數字化制造重點實驗室, 上海 200240;2. 上海飛機制造有限公司 制造工程部, 上海 200436)

幾何精度對機械產品的外觀、性能及其生產效率都有直接的影響, 是衡量產品制造質量的一個重要指標. 作為工件加工、裝配和測量過程的基本環節, 定位過程產生的誤差是最終產品幾何誤差的一個重要來源, 其主要受到2類因素的影響: ① 零部件及工裝夾具上定位基準的制造誤差等上游因素; ② 定位方案等工藝因素. 通過對定位方案的穩健設計, 降低定位誤差對定位基準制造誤差的敏感度, 是提高工件定位精度并最終提高產品制造質量的一種重要手段.

圍繞定位方案穩健設計, 國內外的學者開展了大量的研究. 從剛性零件定位約束的運動學分析入手, 文獻[1-3]中研究了零件的確定性定位和完全約束. 文獻[4-5]中建立了夾具定位點和零件的接觸約束方程, 在此基礎上采用線性微分法建立了三維工件定位誤差分析模型, 為空間三維定位方案的穩健設計奠定了基礎. 在穩健定位方案求解方面, Cai等[4]采用非線性規劃的方法求解三維工件的穩健定位方案； Wang[6]采用試驗設計的方法對定位方案進行了比較和優選； Huang等[7]提出了一種可變順序空間填充算法來搜索定位方案的最優解. 針對工件定位的穩定性, 姜昂等[8]采用遺傳算法搜索最佳定位點； Wang等[9]將穩健性和穩定性同時作為定位方案的優化目標, 比較了遺傳算法和蟻群算法求解多目標優化問題的效果. 針對多工位裝配的定位方案穩健設計, Tian等[10]采用遺傳算法進行求解； Vasundara等[11]提出了一種結合遺傳算法和漢默斯里序列抽樣的2步優化策略； Tyagi等[12]提出了一種基于局部增量算法的啟發式優化算法. 由于三維定位誤差分析模型參數眾多、形式復雜, 所以上述研究多采用數值的方法搜索求解穩健方案. 數值方法的局限性在于只能獲得各設計參數以具體的數值形式表示的特解， 而無法獲得以各參數相互關系式表示的一般解, 因此難以直觀嚴格地揭示共性規律.

本文針對三維空間定位, 結合常用的工程條件和習慣, 在引入2個附加假設對三維定位誤差分析模型進行簡化的基礎上, 對定位方案的穩健性進行解析分析并求解其優化設計的一般解, 以揭示其中的共性規律, 供設計人員參考.

1 三維定位誤差分析模型及其簡化

針對三維工件的6點確定性定位, 在剛性及小位移假設下, 推導了定位誤差與定位參數(6個定位點的位置坐標、控制方向)及定位點制造誤差之間的定量關系[4]:

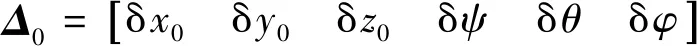
式(1)是一個通用模型, 參數眾多，形式復雜, 很難進行解析上的分析.本文結合常用的工程條件和習慣, 引入2個附加假設對其進行簡化.

假設1定位點垂直于其控制方向的制造誤差可忽略.

[δxiδyiδzi]=

(2)

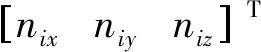
(3)

(4)

把式(2)～(4)代入式(1), 可得

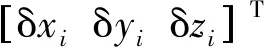
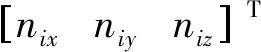
(5)

可見, 垂直于控制方向的誤差對測點誤差的影響可以忽略. 式(1)可簡化為

(6)

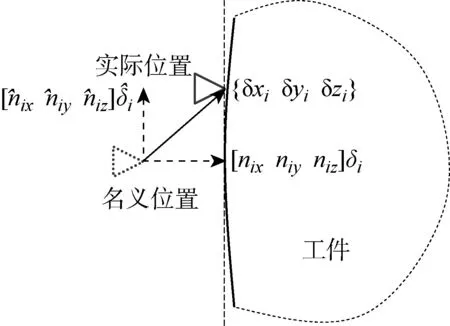
圖1 定位點制造誤差的分解Fig.1 Decomposition of the geometric error at a locator

這一現象的產生是由于在推導式(1)的過程中, 在小位移假設的基礎上以工件在定位點處的切平面來表征工件在該處的實際表面[4]， 假設1實質上是小位移假設的一個延伸.

假設2定位點控制方向與坐標軸方向平行.

為了降低定位點設置不當帶來的影響, 在工程中定位點的控制方向往往設計成與全局或工件坐標系的坐標網格(軸)平行或近似平行[13], 如圖2所示. 這在汽車制造業中稱之為網格平行性準則[13], 本文將該條件作為第2個假設引入.

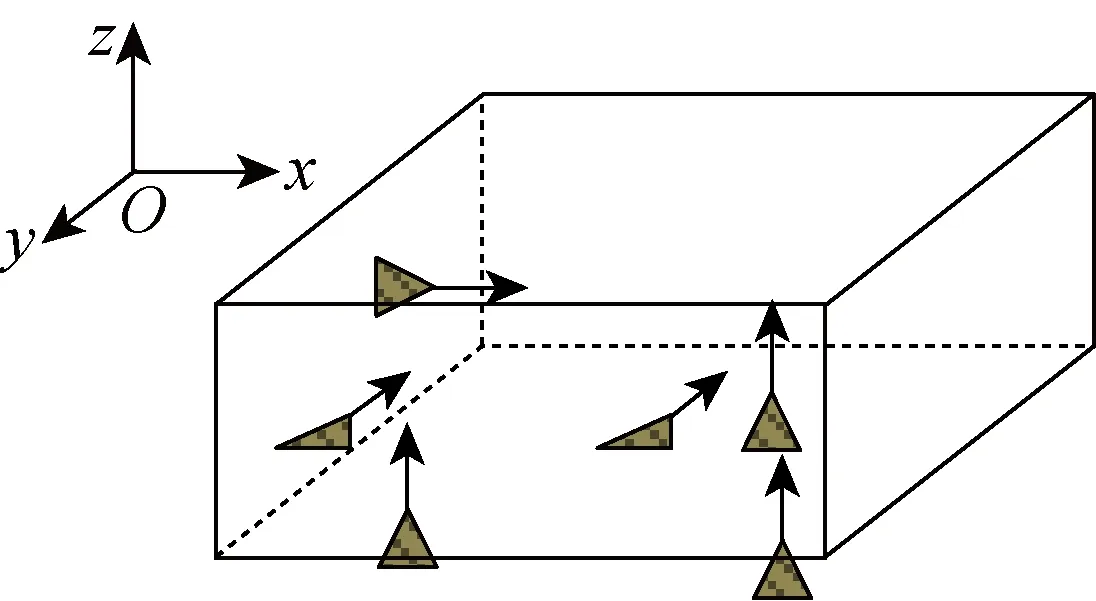
圖2 控制方向平行于坐標軸的定位點Fig.2 Locators with control parallel to the axes of coordinate system

不失一般性地, 假設第1定位方向為z向, 第2定位方向為y向, 第3定位方向為x向. 在本文的后續推導中將沿用此假設. 6個定位點的控制方向具體為

(7)

把式(7)代入式(6), 最終可得

(8)

式(8)相對式(1)形式大為簡化, 設計參數亦由36個減少至12個, 使解析分析和求解成為可能.

2 定位方案穩健性分析及優化設計

對簡化后的Jacobian矩陣求逆, 由式(8)可得

(9)

式中:

2.1 定位方案穩健性的影響因素

由式(9)可知, 工件的定位誤差由定位點的位置以及定位點的制造誤差共同決定, 其中定位點的位置決定了定位方案的穩健性. 根據式(9)的具體形式, 可以得出以下結論:

(1) 在遵循網格平行性準則的情況下, 各個定位點沿其控制方向的位置對工件定位誤差沒有影響. 即式(9)中沒有出現的z1、z2、z3、y4、y5和x6不影響定位方案的穩健性.

圖3所示為沿控制方向定位點的位置變動, 實線定位點和虛線定位點分別表示2套不同的定位方案. 這2套方案的定位點位置只在沿其控制方向上存在差異, 而穩健性則完全相同.

(2) 控制第1定位方向的3個定位點, 沿其控制方向的投影三角形面積不能為0; 控制第2定位方向的2個定位點, 沿第3定位方向的坐標不能相等. 即

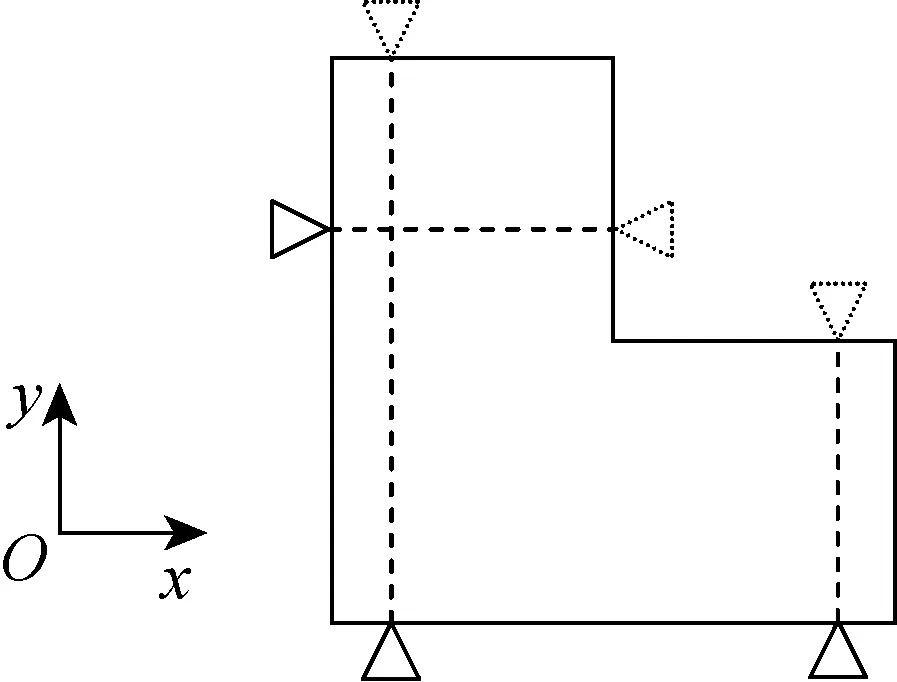
圖3 沿控制方向的定位點位置變動Fig.3 Positional variation of locators along their controlling directions

(x4-x5)(y2x1+y3x2+y1x3-

y1x2-y2x3-y3x1)≠0

(10)

(3) 工件沿第1定位方向的定位誤差只與控制該方向的3個定位點的位置和制造誤差有關; 沿第2定位方向的定位誤差只與控制第1、第2定位方向的5個定位點的位置和制造誤差有關; 沿第3定位方向的定位誤差與所有6個定位點的位置和制造誤差都有關.

(4) 特別地, 對于平板工件, 由于工件本身形狀的特點, 6個定位點沿第1定位方向的坐標滿足

z1=…=z6=z

(11)

把式(11)代入式(9), 可得

(12)

觀察式(12)中的傳遞矩陣可知, 此時矩陣的第1～3列只與控制第1定位方向的3個定位點的位置有關, 矩陣的第4～6列只與控制第2、第3定位方向的另外3個定位點位置有關. 2組定位點之間不存在對定位誤差的交互作用, 其布置優化可分別進行.

2.2 定位方案穩健設計的一般解

本文僅針對單測點的情況, 穩健設計的目標為位于坐標系原點的測點沿3個坐標軸方向定位誤差的波動總和最小.某最穩健定位方案如圖4所示.

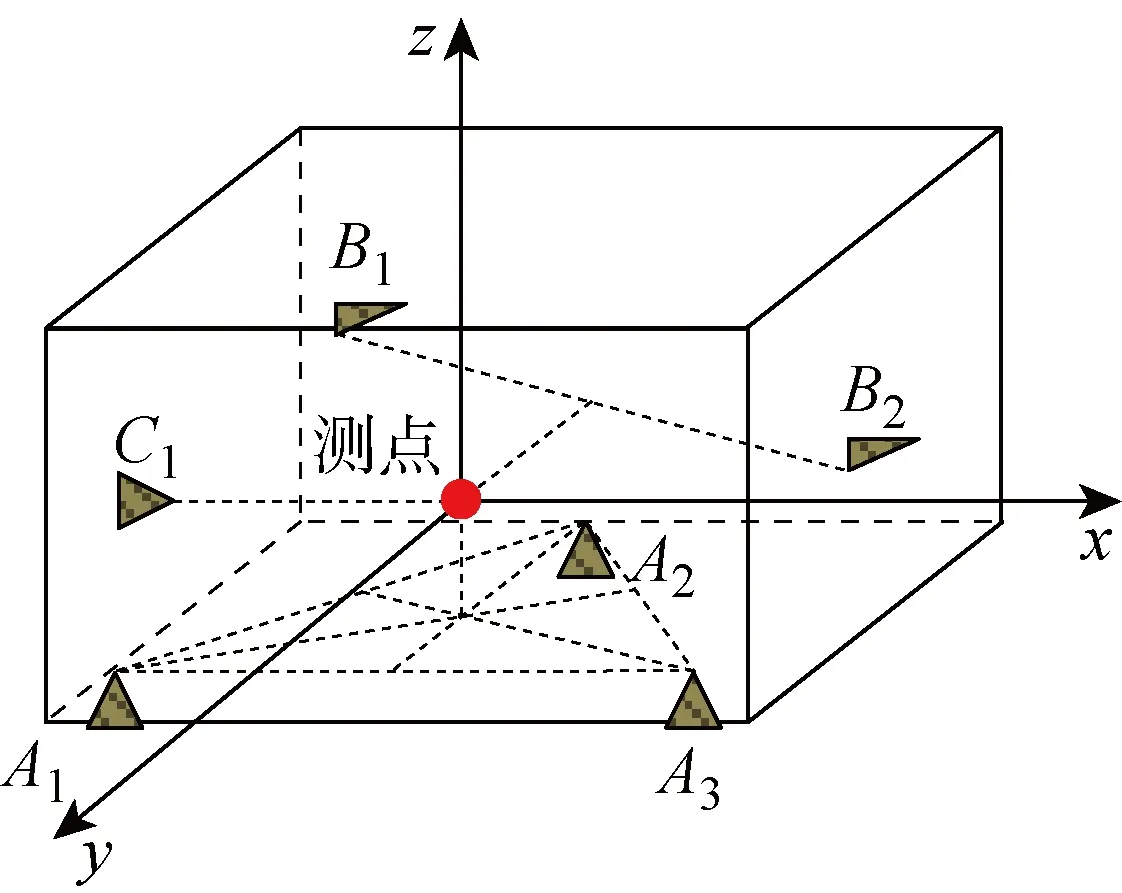
圖4 某最穩健定位方案Fig.4 A most robust locating scheme

假設6個定位點具有相同的制造精度, 沿其控制方向制造誤差的方差D(δi)=σ2, 由式(9)可得

D=D(δx0)+D(δy0)+D(δz0)=

(13)

式中：

ε2=y3x2-y2x3

ε3=y1x3-y3x1

ε4=y2x1-y1x2

(1) 由式(9)和(13)可知, 控制第3定位方向的定位點6, 其坐標y6和z6僅對D(δx0)有影響. 對

(14)

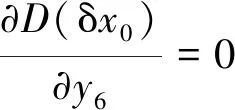
f1y6+f2z6=0，f3z6+f4y6=0

(15)

式中:

f1，f2，f3和f4是與y6和z6無關的函數, 且f1f3≠f2f4, 為保證式(15)成立需滿足

y6=0，z6=0

(16)

式(16)的物理含義為, 控制第3定位方向的1個定位點, 沿該方向的投影與測點重合, 如圖4中的C1點. 將式(16)代入式(14), 等號成立; 將式(16)代入式(9), 第1行的前5個元素為0. 此時, 測點沿該第3定位方向的定位誤差僅與控制該方向的1個定位點有關, 并且其方差D(δx0)取得最小值σ2.

(2) 當式(16)滿足時, 由式(9)和(13)可知, 控制第2定位方向的定位點4和5, 其坐標x4、z4、x5和z5僅對D(δy0)有影響. 對

(17)

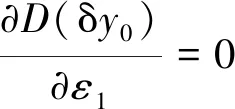
f5ε1=0

(18)

式中:

f5為與變量ε1無關的函數, 為保證式(18)成立，需滿足

ε1=z4x5-z5x4=0

(19)

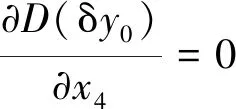
(20)

聯立式(20)中的2個方程并結合式(10), 可得

(21)

進一步可得

x4+x5=0

(22)

式(19)和(22)的物理含義為, 控制第2定位方向的2個定位點, 沿該方向投影線段的中點與測點重合, 如圖4中B1和B2點. 把式(19)和(22)代入式(17), 等號成立; 把式(19)代入式(9), 第2行的前3個元素為0. 此時, 測點沿第2定位方向的定位誤差僅與控制該方向的2個定位點有關, 且其方差D(δy0)取得最小值σ2/2.

(3) 當式(16)、(19)和(22)滿足時, 由式(9)和(13)可知, 控制第1定位方向的定位點1、2、3, 其坐標x1、y1、x2、y2、x3、y3僅對D(δz0)有影響,

在手機應用、互聯網服務器以及運營商核心網引入網絡狀態數據的收集、模型運算以及QoS調用的準入功能,能有效確保用戶感知指標,有利于運營商能力開放業務的順利開展。本文成果主要以手機游戲為應用對象,在移動互聯網中不同

(23)

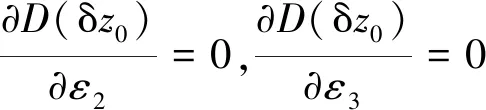
(24)

聯立式(24)中的3個方程并結合式(10)可得

(25)

進一步可得

ε2=ε3=ε4

(26)

將式(26)代入式(23), 等號成立. 由ε2,ε3,ε4的表達式以及式(26)可得

(27)

式(27)的物理含義為, 控制第1定位方向的3個定位點, 沿該方向的投影三角形的形心與測點重合, 如圖4中的A1、A2和A3點. 此時, 測點沿第1定位方向定位誤差的方差D(δz0)取得最小值σ2/3.

需要注意的是, 同時滿足式(16)、(19)、(22)和(27)的最穩健定位方案有無數種, 而圖4中所示的方案只是其中的一種.

3 算例

3.1 某平板工件定位方案比較及VisVSA分析驗證

VisVSA是工程中常用的主流商用3維偏差分析軟件之一, 其算法以Monte Carlo模擬為基礎, 在抽樣次數較高的情況下具有很高的收斂精度. 由3定位塊+1四向銷+1二向銷構成的一面兩銷定位是最經典的定位方式之一, 同時在分析中也易于轉化為6點定位的形式. 本文以采用該定位方式的某平板工件為例, 針對多種定位布置方案, 分別根據前文分析推導得到的結論以及商用3維偏差分析軟件VisVSA的定量分析結果, 對其穩健性進行比較, 以驗證前文結論的準確性.

該平板工件及其定位方案如圖5所示. 坐標系原點設在測點處, 垂直紙面方向為z向; 在分析中, 二向銷和四向銷分別轉化為控制其短軸方向和2個相互垂直方向的定位點, 不考慮孔銷配合間隙; 各定位點的制造誤差皆服從正態分布N(0, 1). 其中：方案1是根據2.2節的分析結論布置的最優定位方案；方案2在方案1的基礎上, 將二向銷的位置沿其控制方向進行了平移. 根據2.1節的分析結論, 定位點沿其控制方向的位置變動對定位精度無影響, 其定位精度應與方案1一致.

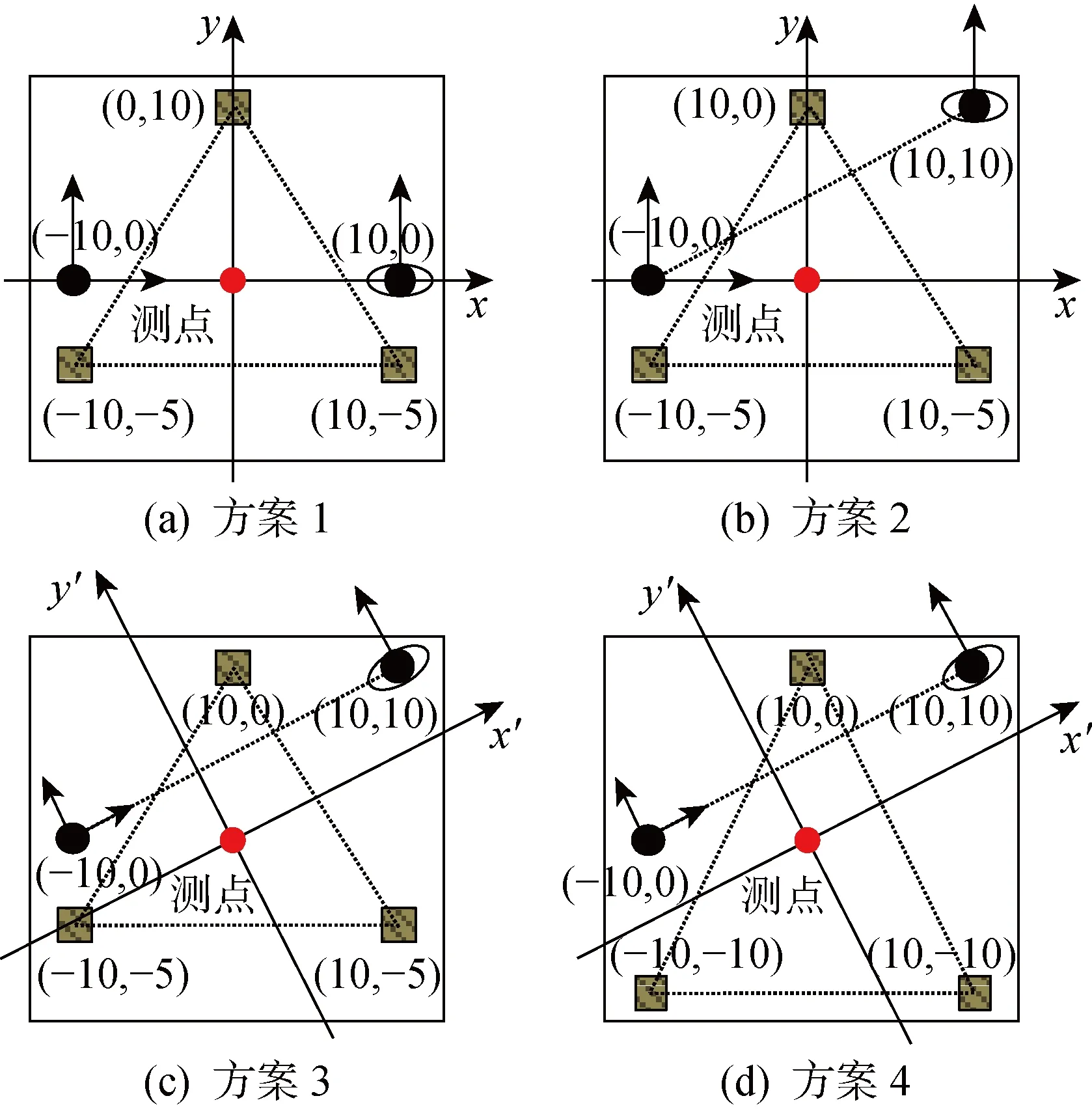
圖5 某平板工件的4種定位方案Fig.5 4 different locating schemes of a plate workpiece

方案4在方案3的基礎上, 對3個定位塊的位置進行了調整, 使投影三角形的形心偏離測點. 根據2.2節的分析結論, 測點沿第1定位方向即z向的定位精度將降低.

利用VisVSA計算這4種方案下的定位精度, Monte Carlo模擬抽樣次數為 5 000 次, 結果如表1

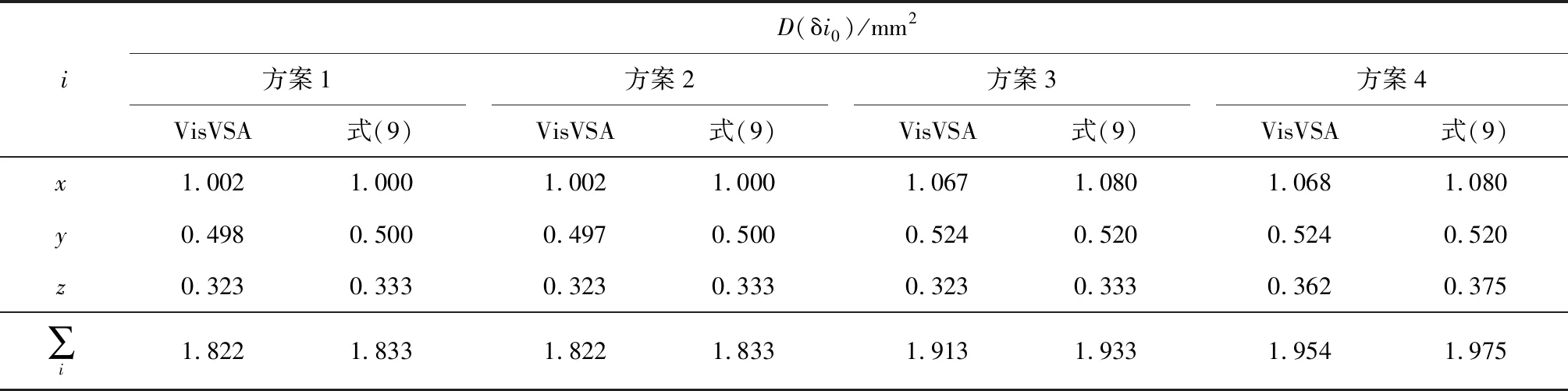
表1 各方案VisVSA及本文方法定位精度分析結果Tab.1 Analyzed geometric variations from VisVSA and the proposed method under different locating schemes

所示. 此外, 表1中同時列出了直接結合式(9)和統計法得到的計算結果.

由表1可見：VisVSA對各方案定位精度的比較結果與本文的比較結果完全吻合；結合式(9)和統計法得到的定量分析結果與VisVSA的定量分析結果也非常接近.

3.2 某飛機后機身沖壓排氣管安裝定位方案優化

利用前文分析推導的結論對某飛機后機身沖壓排氣管的安裝定位方案進行優化. 該沖壓排氣管與上游管道采用軟管進行連接, 配合精度要求不高. 安裝過程存在的主要風險是安裝到蒙皮后因誤差過大而導致的與其前側斜框的間距過小, 這將可能在飛機飛行過程中由于晃動而發生干涉.

當前沖壓排氣管的安裝定位方案如圖6所示. 第1基準為法蘭面A, 第2基準為法蘭面上的定位孔B0, 第3基準為開口中心人工對齊點C0. 以下對其進行優化: 由于結構限制, 其第1基準難以更改; 而根據 2.2 節的分析結論, 應選擇可能干涉方向作為第2定位方向以加強對該方向定位精度的控制, 且控制該方向的2個定位點的布置使得可能干涉位置沿該方向的投影盡量靠近兩定位點的中點. 優化后的第2、第3基準為圖6中的B、C點, 分別為法蘭面上的2個定位孔.

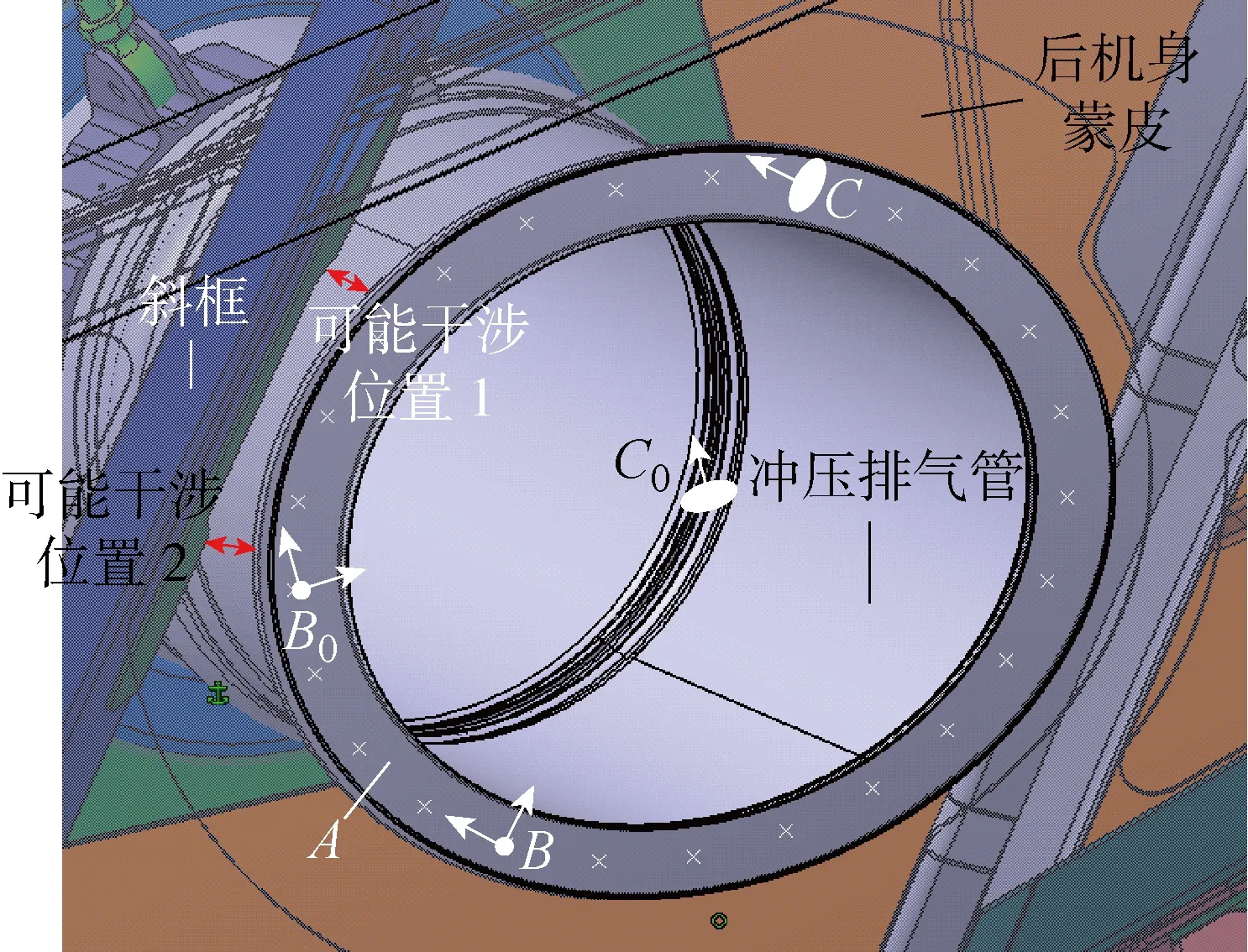
圖6 某飛機后機身沖壓排氣管Fig.6 A stamp exhaust pipe at the rear fuselage

為了驗證優化效果, 利用VisVSA分別對2種方案進行裝配精度分析. 主要模擬參數: 后機身包括蒙皮和斜框加強件作為基件, 沖壓排氣管作為被安裝件; 各零件相關關鍵特征的公差如表2所示.表中: 蒙皮和斜框加強件的公差為其在后機身部件狀態下的公差; 可能干涉位置的配合間距要求不小于4 mm; Monte Carlo模擬抽樣次數為 5 000 次. 另外, 為了使定位方案本身更具可比性, 在原方案的模擬中將開口中心人工對齊點的位置度公差參照定位孔亦分別設置為1和 0.5 mm.

在VisVSA中建立的模型及其分析結果如表3所示. 在對其他參數不作調整, 僅對第2、第3基準的位置進行優化的情況下, 兩處可能干涉位置配合間距的超差率和標準差都有所降低.

表2 各零件關鍵特征公差

Tab.2 Assigned tolerances on the key characteristics of the mating parts

零部件關鍵特征制造公差/mm蒙皮 內形面輪廓度5排氣管定位孔位置度1開口中心人工對齊點位置度2斜框加強件外表面輪廓度2法蘭面輪廓度1沖壓排氣管定位孔位置度0.5開口中心人工對齊點位置度1排氣管外表面輪廓度1

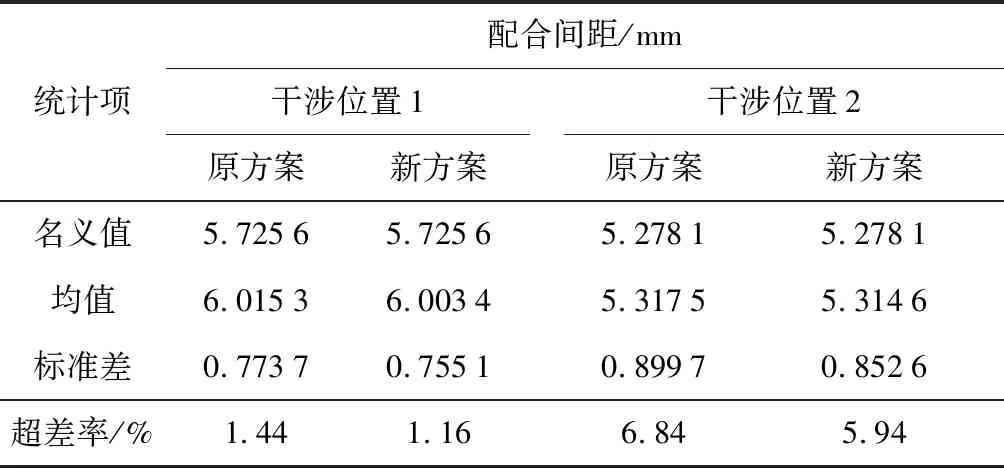
表3 VisVSA裝配精度分析結果Tab.3 Analyzed assembly variations from VisVSA

4 結語

現有關于三維定位方案穩健設計的研究多使用數值方法進行求解. 數值解法適應性強, 而解析分析及通過解析分析獲得的一般解能更直觀嚴格地揭示共性規律. 本文結合常用的工程條件和習慣引入2個附加假設, 在對三維確定性定位誤差分析模型進行簡化的基礎上, 用解析的方法分析了定位方案穩健性的影響因素, 并針對單測點的定位誤差控制, 求解了定位點最穩健布置的一般解.此外，得到了以下一些三維工件空間定位方案穩健設計的一般規律:

(1) 在遵循網格平行性準則的情況下, 各定位點沿其控制方向在何處布置對定位精度沒有影響;

(2) 定位點沿其他2個方向的最佳位置, 應使得控制同一方向的各定位點沿該方向的幾何投影形心與測點重合;

(3) 在滿足規律(2)且假定各定位點制造精度相同的情況下, 測點沿第1定位方向的定位精度最高, 第2定位方向次之, 第3定位方向最低, 其比例關系為1/3∶1/2∶1.

掌握這些規律可以幫助工程技術人員理解、評估設計方案的影響, 從而設計出更為穩健的定位方案.