鋁合金車身窗框亮條翻邊圓角不均勻缺陷解決方案

詹 楊， 趙亦希， 朱寶行

(上海交通大學 上海市復雜薄板結構數字化制造重點實驗室， 上海 200240)

近年來，隨著汽車行業的快速發展和人民生活水平的提高，人們對汽車外觀提出了越來越高的要求，各大汽車廠商也開始著眼于提高車身的美觀性.車身窗框亮條作為裝飾性的汽車配件，在汽車上應用越來越廣泛.為滿足裝配需求，車身窗框裝飾條需要進行端頭局部翻邊成型.

以某車型為例，車身窗框亮條形狀復雜，外形尺寸約為1 000 mm×30 mm，厚度約為1 mm，沿寬度方向截面較窄，為復雜的變曲率凸截面，在翻邊成型過程中，易產生圓角不均勻缺陷，翻邊后亮條產品脊部圓角半徑較大，向兩端圓角半徑逐漸減小.不均勻的圓角半徑嚴重影響了車身窗框裝飾亮條的質量，需要后續耗費大量的人力來進行打磨和拋光，是亟待解決的問題之一.

國內外很多學者對翻邊工藝進行了研究，在缺陷及改進方法方面，Port等[1]研究了汽車車門翻邊過程中出現的表面缺陷及其預測方法.韓東風等[2]研究發現內凹型翻邊是造成圓弧曲面不光順的原因，其中圓弧過渡區所受周向的剪應力是不光順產生的誘因.申偉等[3]研究發現凸曲面直翻邊存在A面不平，B面起皺、疊料問題，通過改變產品造型和調整刀塊形狀解決了缺陷問題.孫苗苗等[4]通過在變形金屬與模具間加一層導熱性較差的非金屬材料，以及在翻邊金屬變形區外加了一層塑性較好的金屬,解決了塑性差的不銹鋼件沖孔翻邊時開裂的問題.張凌云等[5]針對航空中框肋零件等凸翻邊零件，研究了網格劃分、摩擦系數、加載速率對成型零件凸翻邊部分起皺及其回彈過程的影響.許天宇[6]分析翻邊開裂的原因及影響因素，通過增大拉延高度和降低翻邊高度,減小翻邊區域材料變形程度,解決了拉延翻邊的開裂問題.在工藝參數對翻邊影響方面，謝暉等[7]研究了上彎曲半徑、下彎曲半徑、翻邊角度等特征參數和潤滑條件、模具間隙兩個工藝參數對翻邊及其回彈過程的影響.高鵬[8]研究了各種幾何參數對不同類型翻邊工藝中變形區邊緣最大切向應變的影響規律.孫澤[9]研究了平面曲線翻邊過程中應力應變的變化規律，分析了材料參數、零件幾何尺寸以及工藝參數等因素對畸變的具體影響，并分析得到了畸變的分布規律.總的來說，現有研究多針對零件平直翻邊及理想V形件、筒形件等均勻曲率零件的曲面翻邊，對于窄坯料變曲率截面零件局部翻邊工藝研究較少，所得結論難以直接應用到車身窗框亮條這類變曲率截面零件.

本文針對車身窗框亮條翻邊過程中出現的圓角不均勻問題，結合其外形特點和工藝過程，建立有限元模型，研究工藝參數對翻邊質量的影響，提出針對圓角不均勻問題的合理解決方案，并進行試驗驗證.

1 亮條翻邊有限元模型

1.1 有限元模型的建立

1.1.1材料參數 翻邊材料采用5657-T態鋁合金，厚度為 0.8 mm，在Zwick萬能材料試驗機上進行了室溫單向拉伸試驗，獲得材料應力應變曲線，并經數據處理獲得真實應力應變曲線，如圖1所示.擬合得到材料的材料力學性能參數如表1所示.

采用Hooke定律和Ludwik硬化方程來描述材料的彈塑性力學行為，其數學表達式為

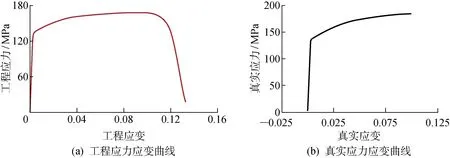
圖1 5657-T室溫拉伸曲線Fig.1 Tensile curve at room temperature for 5657-T

表1 5657-T態鋁合金力學性能Tab.1 Mechanical properties of 5657-T aluminum alloy

σel=Eεel

(1)

(2)

式中：σ0為材料的屈服應力；εel、εpl分別為材料的彈性真應變和塑形真應變；σel、σpl分別為材料的彈性真應力和塑性真應力；E為彈性模量；強度系數K、硬化指數n和屈服應力σ0通過室溫下單向拉伸試驗得到的數據擬合而得，K=185.9 MPa，n=0.546 6，σ0=138.0 MPa.

1.1.2翻邊模型建立 采用Dynaform軟件對端頭翻邊這一步工序進行模擬，并忽略之前工序造成的內應力.亮條尺寸為1 000 mm×20 mm×0.8 mm，如圖2所示，將坯料截斷為50 mm×20 mm×0.8 mm.

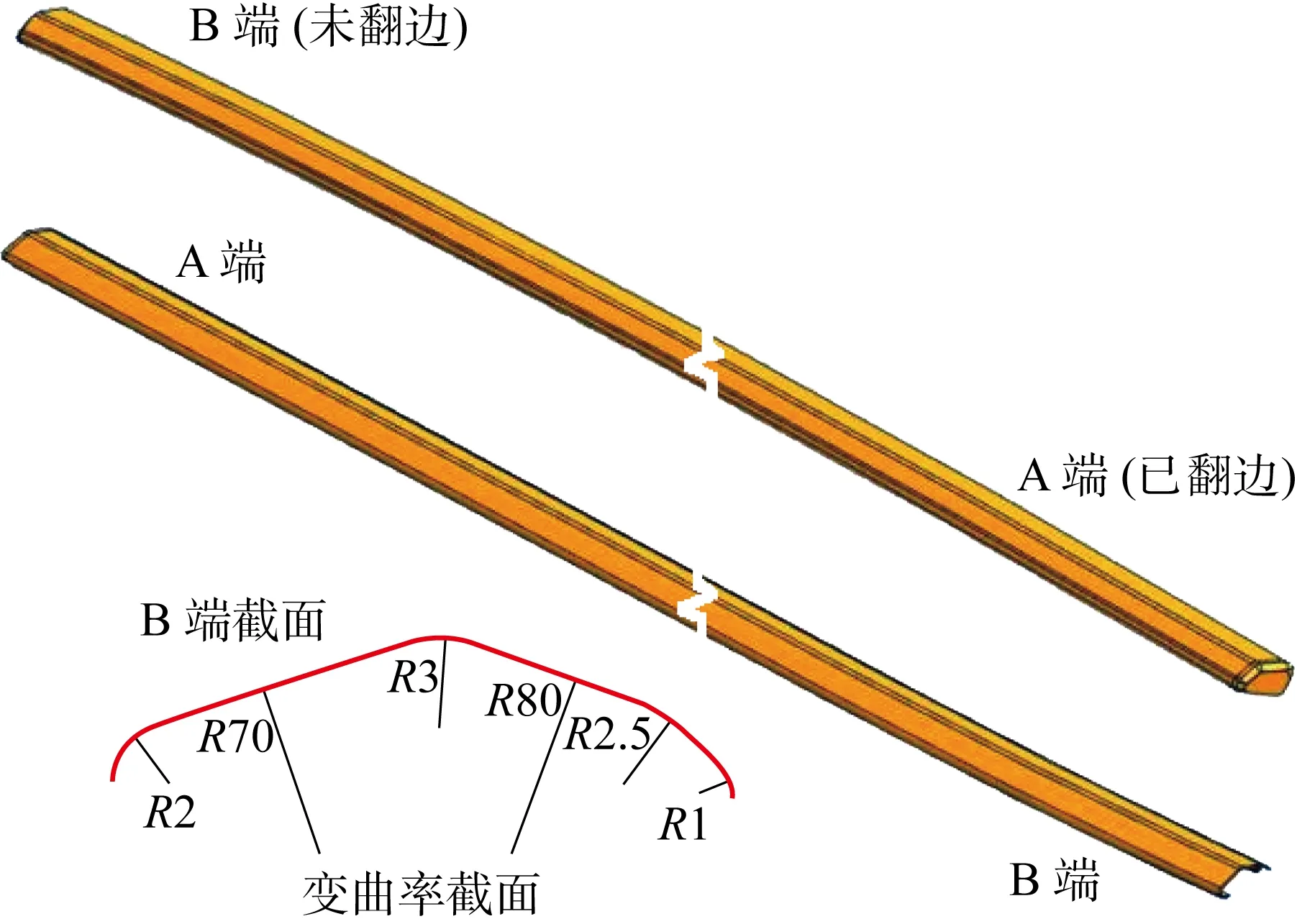
圖2 亮條幾何示意圖(mm)Fig.2 Geometry illustration of window trim strip (mm)

圖5 圓角半徑測量方法Fig.5 Measuring method of fillet radii

由于亮條長寬比大，翻邊端頭寬度方向上尺寸很小，為保證模擬精度以及效率，對網格進行分區域劃分.采用Hypermesh軟件前處理功能對坯料網格進行劃分，將坯料分為3個部分；壓邊區域A、圓角過渡區B和翻邊區域C.區域位置及其大致尺寸如圖3所示，其中壓邊區域A不是主要變形區，劃分為2 mm的網格；圓角過渡區B材料所受應力大，變形劇烈， 易產生缺陷，網格尺寸選取為 0.3 mm，由于板料所受拉伸力大致垂直于翻邊線，將區域B網格平行于翻邊線劃分；翻邊區域C由于要關注此部分的厚度分布及變化情況，采用 0.5 mm的網格.以上所有網格均采用四邊形網格.模型采用Dynaform中36號材料模型，采用的是Barlat89屈服準則；選取了BT單元，厚向積分點選擇為9個點.

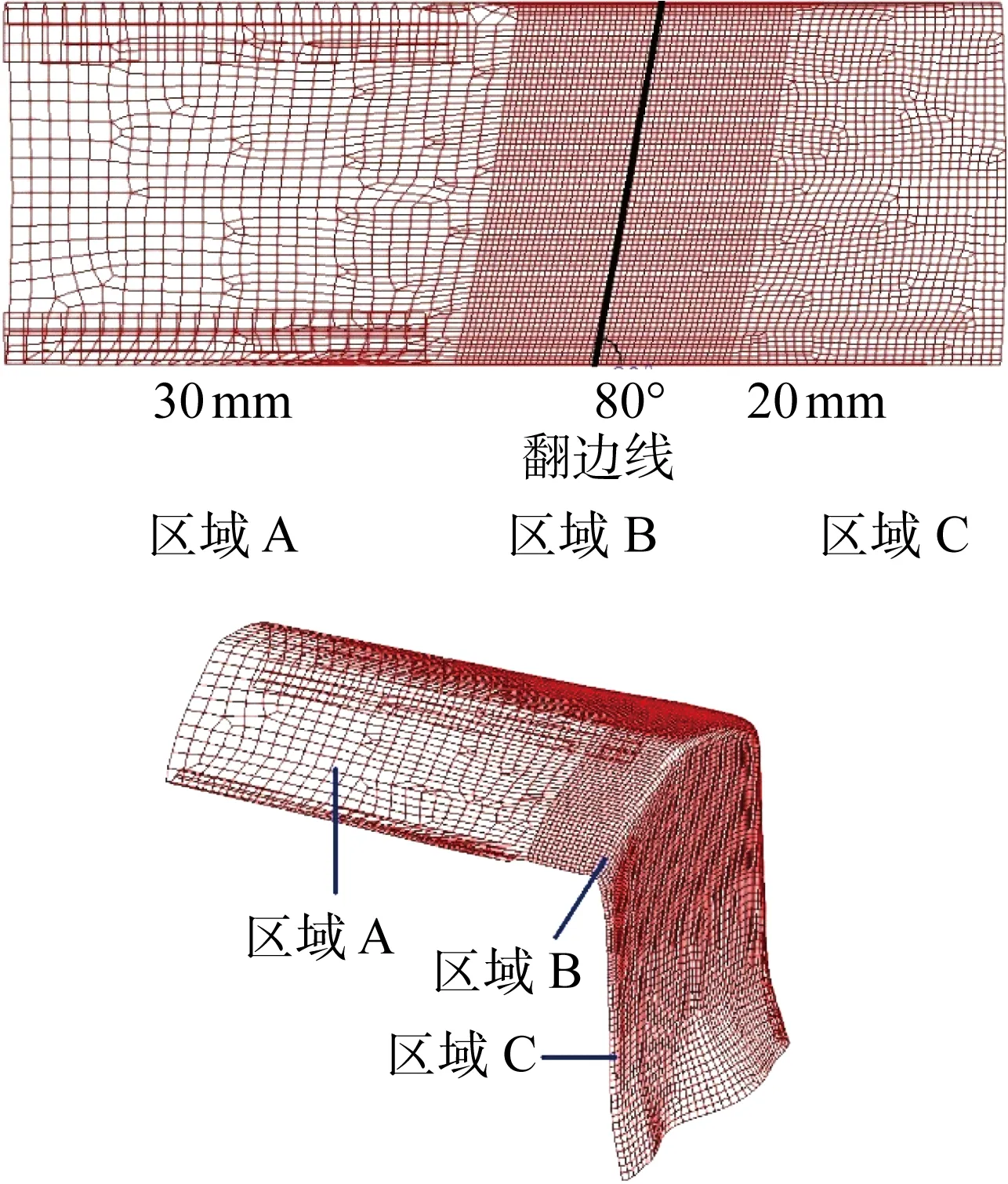
圖3 網格劃分區域示意圖Fig.3 Mesh area division

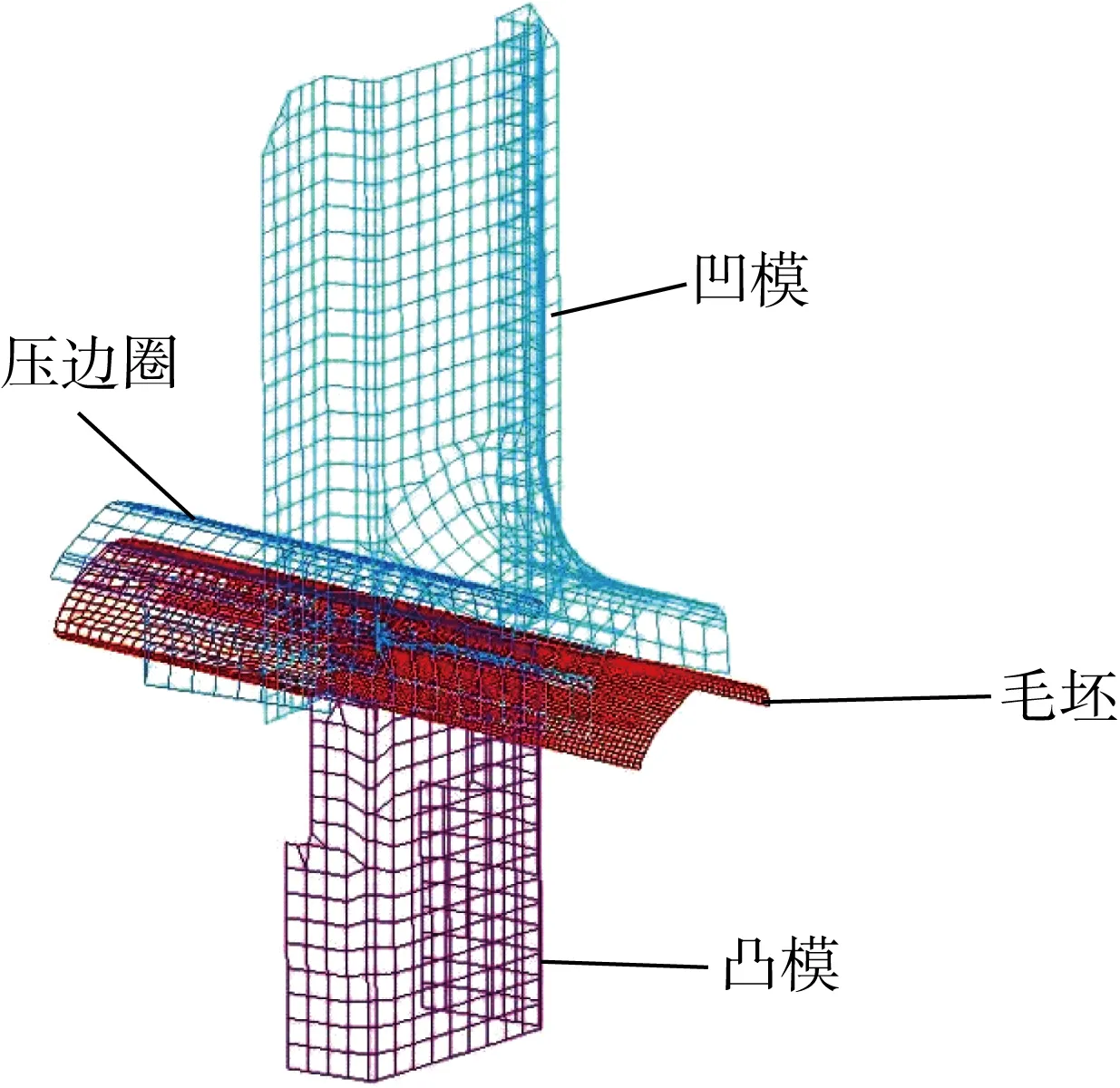
圖4 數值模擬模型Fig.4 Numerical simulation model

綜合以上的選擇，最終模型圖4所示，其中工藝參數采用實際生產所用參數：凹模半徑為 0.2 mm，凸模半徑為3 mm，凹凸模間隙為 0.7 mm.

1.2 有限元模型可靠性驗證

在有限元模型上，等間距選取亮條上7個豎直截面與坯料相交，測量這7個截面內圓角區域的翻邊圓角半徑.為保證每次測量的穩定性和客觀性，利用Dynaform軟件中后處理軟件選取、保存截面的功能，保證每次選取截面相同(圖5(a)).

模型圓角半徑測量方法：為了準確測量變形區內圓角半徑，利用Dynaform后處理軟件在圓角過渡區圓弧范圍內均勻選取并6個點并導出其坐標，如圖5(b)所示；并用MATLAB軟件編程用最小二乘圓法擬合這些點，求出該截面翻邊圓角半徑.如圖5(c)所示，所選截面擬合點擬合效果較好，測得數據可信度較高.

實際產品圓角半徑測量：采用精度為 2.5 mm，量程為1～7 mm的半徑規對圓角半徑進行測量.

如表2所示，模擬測量結果與實際產品(圖6)的測量結果存在一定的誤差，但誤差均小于15%，在合理范圍內，可證明此模型的正確性以及前面忽略內應力假設的合理性.其中表2實際測量所選取的截面位置如圖6所示，模擬測量中所選取截面與實際零件相同.

表2 圓角半徑模擬測量結果與實際零件測量結果對比

Tab.2 Comparison of measured fillet radii between simulation and real products

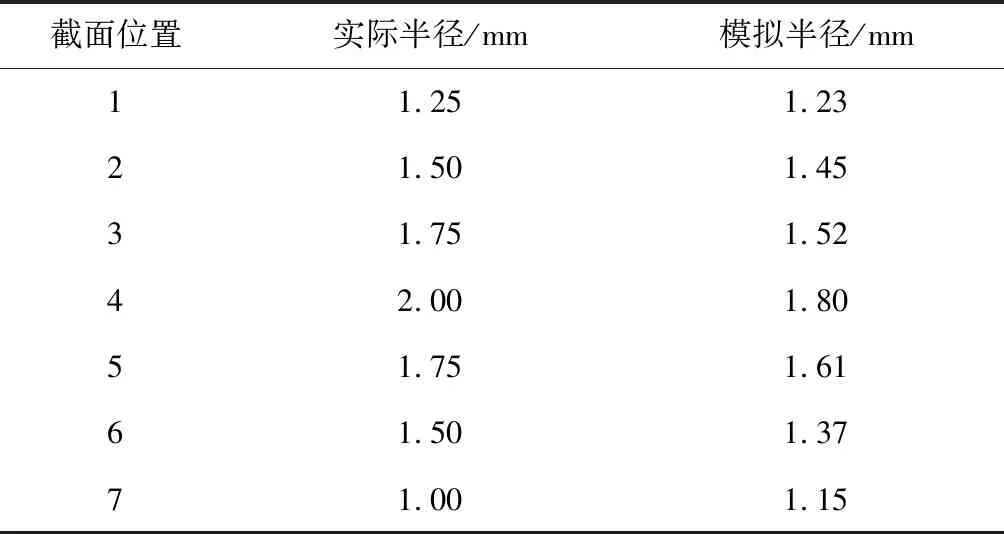
截面位置實際半徑/mm模擬半徑/mm11.251.2321.501.4531.751.5242.001.8051.751.6161.501.3771.001.15

圖6 實際零件測量截面位置Fig.6 The measurement sections of supplied window trim strip

2 工藝參數對翻邊圓角不均勻缺陷影響

從測量的圓角半徑數據(見表2)可以發現，在某型號亮條翻邊過程中，如果采用恒定圓角半徑的凹模，會導致翻邊件圓角半徑不均勻.為了解決圓角不均勻缺陷，需要研究工藝參數對缺陷的影響規律.

根據與生產廠商交流以及模擬嘗試，在實際生產中，對亮條缺陷影響較大，且易于工人調節變換的工藝參數主要為凹模圓角半徑、凸模圓角半徑、凹凸模間隙、壓邊力以及沖壓速度.

其中，工廠常用壓邊力約為5 kN，將壓邊力取3、5和7 kN分別進行模擬，結果顯示，翻邊后的厚度分布幾乎沒有變化，應變也僅有微小區別，可以忽略不計，如圖7所示.關于沖壓速度，工廠實際生產的翻邊沖壓速度為50 mm/s，將沖壓速度取50、100和200 mm/s分別進行模擬，結果顯示，翻邊后的厚度分布幾乎沒有變化，應變也僅有微小區別，如圖8所示，即在實際生產的調節范圍內，沖壓速度對成型結果的影響可以忽略不計.

綜上所述，此處選取凹模圓角半徑、凸模圓角半徑和凹凸模間隙3個工藝參數作為研究內容.根據實際生產中工藝參數的波動范圍，設計了如表3所示的3參數3水平正交試驗，以測量工藝參數的改變對圓角不均勻缺陷的影響.

如圖9所示，正交試驗研究的因素中，凹模圓角半徑對翻邊產品翻邊圓角半徑不均勻缺陷影響非常顯著，敏感性較高，其他工藝參數敏感性較低，影響不明顯，所以后續重點研究凹模半徑的影響.

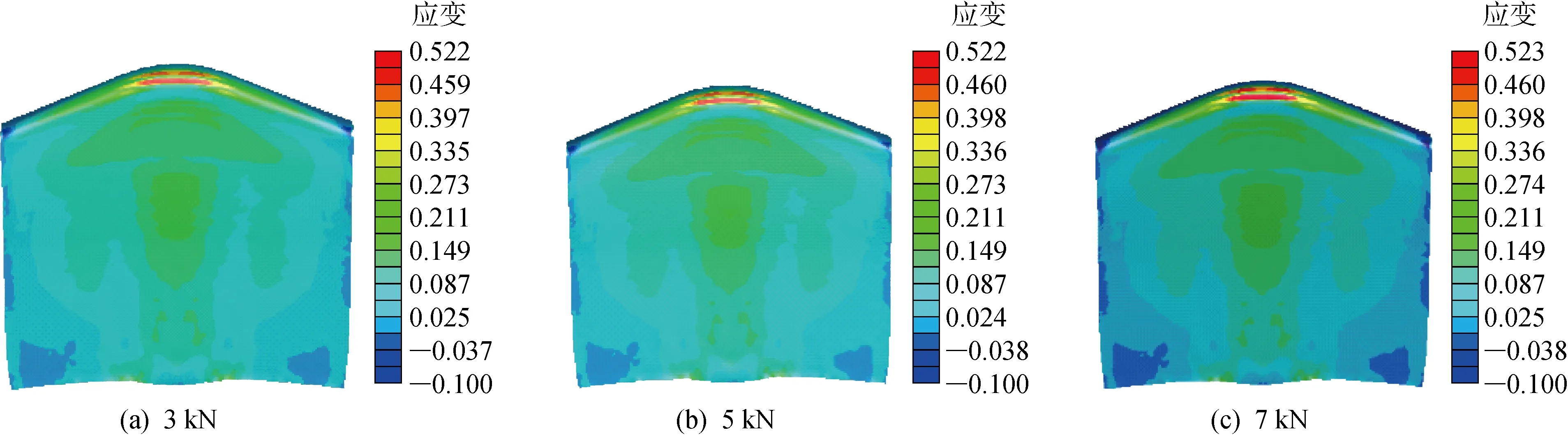
圖7 不同壓邊力下應變對比Fig.7 Deformation comparisons under different blank holder forces

圖8 不同沖壓速度下應變對比Fig.8 Deformation comparisons under different punching speeds

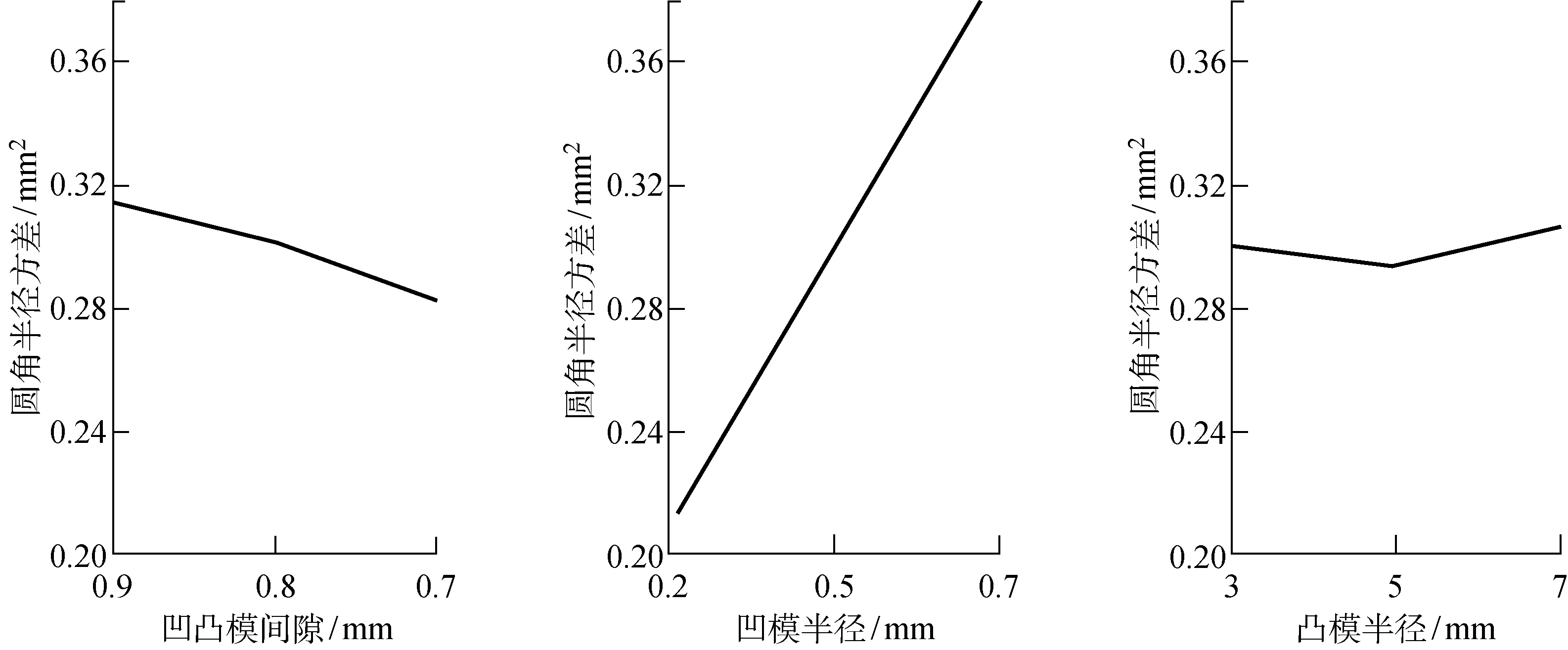
圖9 工藝因素對圓角半徑方差的影響Fig.9 Effects of industrial parameters on variance of fillet radius

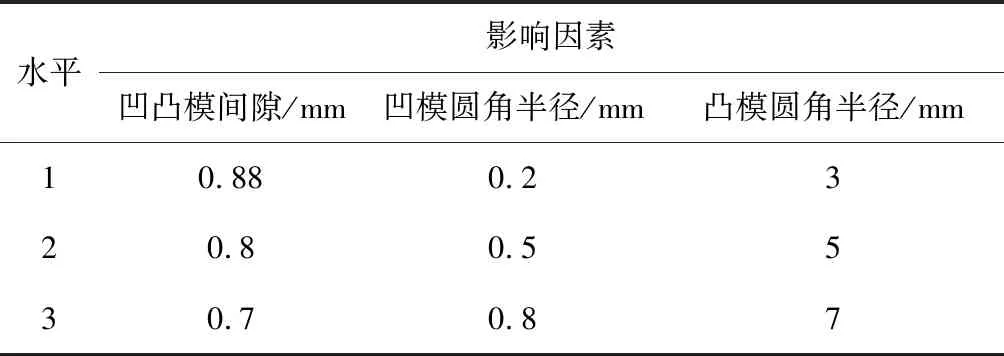
表3 正交試驗影響因素及水平Tab.3 The influencing factors and levels of orthogonal test

對凹模半徑的影響做了進一步的單因素模擬研究，設計凹模半徑分別為 0.2、0.5和 0.8 mm，設定凹凸模間隙 0.7 mm，凸模圓角半徑3 mm.分析翻邊亮條產品圓角半徑在不同截面的分布情況和平均值，分析結果如表4所示.

圖10為凹模圓角半徑對圓角不均勻缺陷的影響，可總結規律如下：① 隨著凹模圓角半徑的增加，產品圓角半徑也隨著顯著增加；② 采用均勻圓角半徑凹模，僅通過調整凹模圓角半徑大小無法將亮條產品的圓角不均勻缺陷控制在肉眼不可見的范圍(極差小于 0.25 mm)；③ 隨著凹模圓角半徑的減小，翻邊亮條產品的方差、極差逐漸減小，圓角不均勻缺陷有所減輕.

表4 不同凹模對應亮條圓角半徑分布Tab.4 Distribution of product’s fillet radius with different dies

圖10 凹模圓角半徑對圓角不均勻缺陷的影響Fig.10 Effect of die fillet radius on uneven fillet radius defect

3 變圓角半徑凹模解決方案

根據前文所得結論，凹模圓角半徑可以顯著影響產品圓角半徑.基于這一結論，針對圓角不均勻缺陷提出變圓角半徑凹模的解決方案：通過對翻邊凹模不同位置圓角半徑的合理規劃，設計一個與缺陷趨勢相反，兩端圓角半徑較大，中間圓角半徑較小的變半徑凹模，使成型亮條的圓角半徑變得相對均勻.

3.1 設計方法及流程

由于亮條的結構特點，對應變圓角半徑凹模應設計為中間圓角半徑較小，兩端圓角半徑較大.以下以半徑為 0.2 mm的凹模介紹具體設計流程.

3.1.1對常半徑凹模模擬并計算變半徑凹模圓角半徑分布 凹模模擬結果對應的翻邊件圓角半徑分布如表5所示，對常半徑凹模進行補償，計算得到變半徑凹模兩側圓角半徑.

表5 凹模對應圓角半徑分布Tab.5 Fillet radius distribution of die

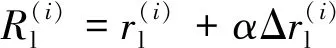
(3)

(4)

式中：R為變半徑凹模圓角半徑；r為翻邊件測量所得圓角半徑；下標r、l分別表示亮條右側、左側；上標i表示第i次模擬迭代過程；α為迭代系數，該系數若過小，則要達到合格圓角半徑極差的迭代次數會變多，該系數若過大，則有可能導致迭代過程不收斂，無法達到合格圓角半徑極差，所以此處取α=1.

作為第1次迭代過程，具體計算如公式為

0.2+(1.8-1.23) mm≈0.8 mm

(5)

0.2+(1.8-1.16) mm≈0.8 mm

(6)

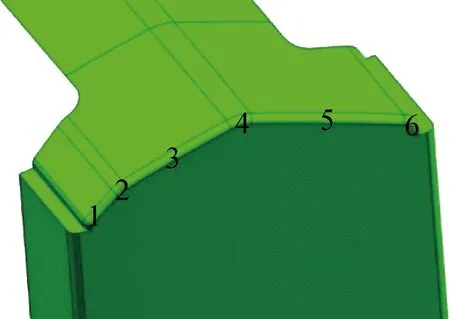
圖11 變半徑凹模不同區域示意圖Fig.11 Different areas of variable radius die

第1次迭代后，變半徑凹模設計1左右側半徑均為 0.8 mm.變半徑凹模按曲率變化分為6個區域(圖11).由于1、2、4、6區域較小，采用均勻凹模圓角半徑.3、5區域采用線性變化的凹模圓角半徑，具體區域半徑計算方法見表6.線性變化按照下式進行：

R(x)=R1+R2l(x)/l0

(7)

式中：R(x)表示距離區域左端x弧長處圓角半徑；R1、R2分別表示區域左端、右端圓角半徑；l(x)表示距離區域左端圓弧長度；l0表示區域圓弧長度.

3.1.2多次模擬迭代獲得滿足缺陷臨界值要求的變半徑凹模 如表5所示， 變半徑凹模設計1凹模對應圓角半徑分布極差為 0.41 mm，沒有滿足極差在 0.25 mm以下的需求.對由 3.1.1 中變半徑凹模設計1再次模擬，獲得半徑分布(表5)后，同樣利用式(5)和(6)計算獲得變半徑凹模設計2，其圓角半徑計算方法如表6所示.對變半徑凹模設計2，再次模擬后，圓角半徑極差已滿足合格產品要求(表5)，小于 0.25 mm.

表6 變半徑凹模圓角半徑計算方法Tab.6 Calculation method of variable fillet radius of the die

3.2 設計流程總結與分析

根據設計流程，在獲得常半徑凹模模擬結果之后，一共進行了2次變半徑凹模設計迭代，達到了預定目標.整個設計流程變半徑凹模設計如表7和8所示，凹模幾何模型如圖12所示.

模擬數據顯示，采用變半徑圓角凹模(凹模圓角半徑最小處為 0.2 mm，最大處為 1.2 mm)的方法，其表征不均勻性的方差由 0.20 mm2減小到了 0.06 mm2，極差由 0.63 mm減小到了 0.19 mm，具有明顯效果.至此獲得了滿足產品要求的變半徑凹模，具體設計流程如圖13所示.

表7 凹模圓角半徑分布Tab.7 Distribution of die’s radius

表8 變半徑凹模設計測量結果Tab.8 Measurement of variable radius die

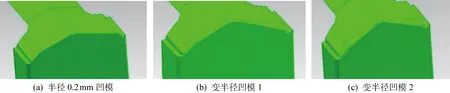
圖12 凹模示意圖Fig.12 Illustration of different dies

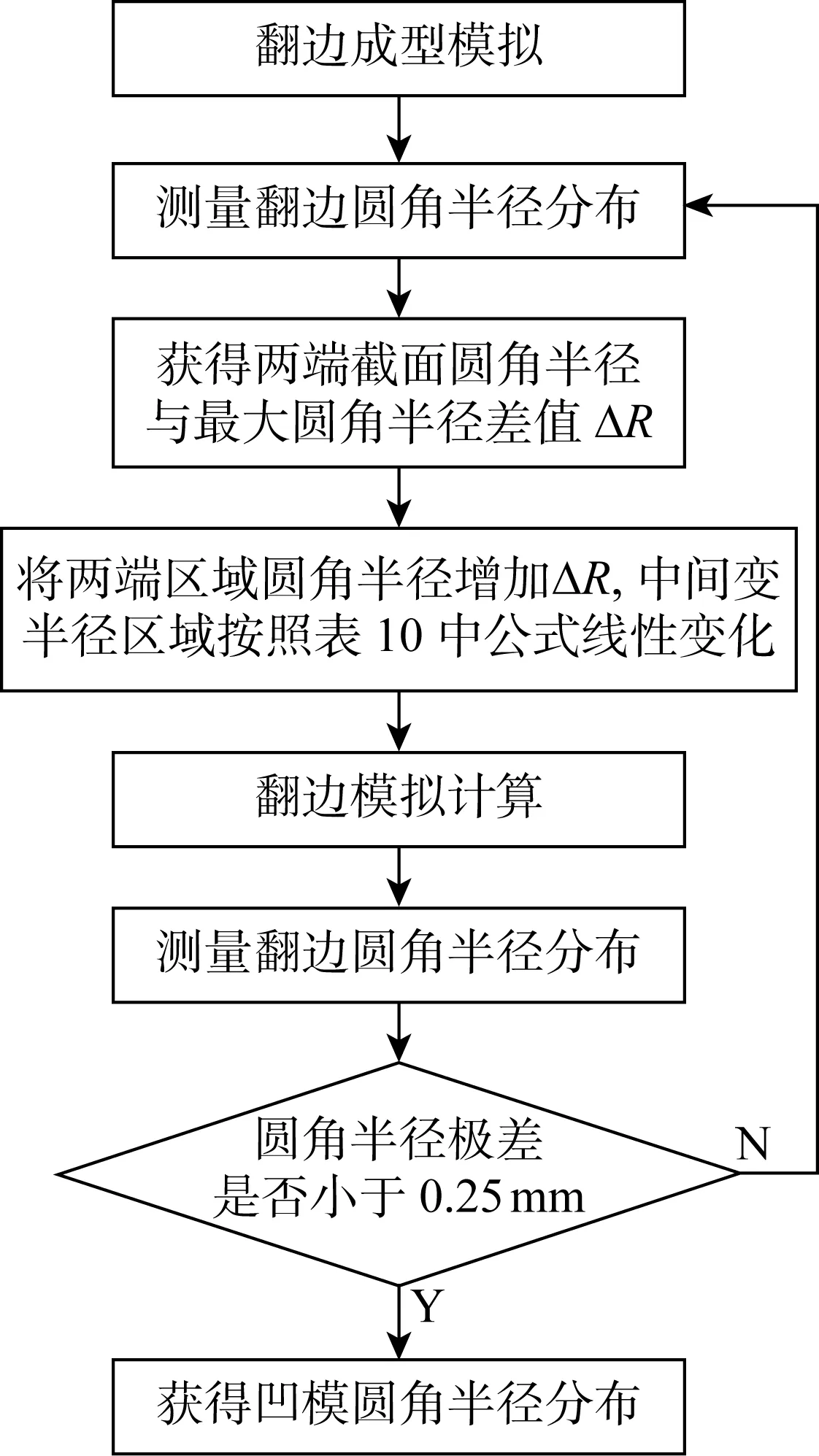
圖13 變半徑凹模設計流程圖Fig.13 Flowgraph of the variable radius die’s design

表9 試驗翻邊件圓角半徑測量結果Tab.9 Measurement results of flanging part fillet radii

4 特征試驗驗證

4.1 特征試驗模具設計及工藝參數

設計了應用于單向拉伸試驗機上的鑲塊化特征試驗模具來進行試驗研究，如圖14所示.圖15所示為通過該特征試驗模具進行翻邊后的亮條產品.

圖14 試驗模具實物圖Fig.14 Pictures of mold

該試驗裝置通過單向拉伸試驗機的軸向力提供翻邊力并控制翻邊速度，通過導套、導柱引導裝置運動方向，完成翻邊成型.為平衡導柱、導套受力，將其設置為沿模具中面對稱分布，同時使單向拉伸試驗機施加的力與上模在翻邊過程中產生的翻邊力共線，減小裝置所受力矩.為了保證加工精度，確定模具、板料位置，采用兩組定位銷來固定凹模、凸模與上、下模板的相對位置，并采用坯料定位塊限制坯料沿寬度方向的位移.同時，在凸模后設置了止動塊來限制凸模的位置，防止凸模因翻邊力過大而向外傾斜，導致凹、凸模間隙發生改變.試驗中工藝參數：凸模半徑為3 mm,凹凸模間隙為 0.7 mm，沖壓速度為500 mm/min.

4.2 試驗結果

試驗設計了4個凹模鑲塊用來驗證提出的變半徑凹模解決方案，分別為 0.2 mm、0.5 mm、0.8 mm和變半徑凹模鑲塊，保持其他工藝參數不變，分別進行翻邊試驗并測量所得產品的翻邊圓角半徑分布，具體結果如表9所示.

試驗結果測量數據如表9所示.由前3組數據結果可知，隨著凹模圓角半徑的增加，翻邊產品半徑也顯著增加.另外，利用了變半徑凹模的方法后，產品不同界面上的圓角半徑分布明顯變得更加均勻，極差值從 1.0 mm減小到了 0.5 mm，且除兩端區域，中間大部分區域極差值都控制在了 0.25 mm之內，基本達到了將極差控制在 0.25 mm以內的目標；方差也從 0.35 mm2左右降低到了 0.16 mm2，圓角不均勻問題得到了顯著改善.

如圖16所示，左側為使用常規恒定半徑凹模成型的亮條產品，樣品中間圓角半徑大，兩側圓角半徑小，存在圓角不均勻缺陷；右側為使用變半徑凹模成型的翻邊亮條樣品，兩側的圓角半徑有所增大，導致整體的翻邊圓角半徑均勻性得到了明顯的提升.

圖16 原翻邊產品與改進后翻邊產品對比Fig.16 Comparison between original and revised product

5 結論

(1) 針對車身窗框亮條這類變曲率零件翻邊，若采用均勻圓角半徑的凹模，翻邊產品可能出現兩端圓角半徑小，中間圓角半徑大的缺陷，難以通過調整工藝參數改善缺陷.

(2) 通過研究凹模半徑、凸模半徑、凹凸模間隙3個工藝參數對圓角不均勻問題的影響，其中主要影響因素是凹模圓角半徑，圓角凹模半徑越小，亮條產品的圓角半徑極差、方差、平均值越小.

(3) 針對圓角不均勻缺陷，提出變半徑凹模的解決方法，建立了變半徑凹模設計流程.通過對凹模圓角半徑進行合理的規劃，可以改善產品的圓角不均勻缺陷，將其圓角半徑極差控制在企業要求的 0.2 mm范圍內，達到生產質量要求.