MIC與傳統相關分析方法比較研究*

梁 珊

(華南理工大學廣州學院，廣東 廣州 510800)

大數據時代，傳統的相關分析方法已不能滿足對數據的探索以及認知需求，隨著計算機技術的提升，大量新的相關分析方法產生，MIC作為目前為止最具有代表性，發展最快，認同度最高的大數據相關分析方法被廣泛使用。本文總結相關分析的發展史，在此基礎上比較研究MIC的適用范圍、測度效果、解釋能力及計算速度，分析其優缺點，以避免使用過程中的誤用。

一、MIC概述

Reshef(2011)指出大數據中度量相關性的統計量應該具有“普遍性”和“均等性”。并給出MIC方法。MIC主要思想是：如果兩個變量之間存在著相關關系，那么在變量的散點圖中可以繪制網格線，通過網格線將隨機變量數據集進行劃分，形成網格，計算變量之間的相關關系就是在每種網格劃分方式下，計算變量數據集的互信息，然后歸一化互信息來確保在不同劃分方式下的互信息值可以做比較。最大相關系數就是在各種網格劃分方式下，互信息的最大值。

可以證明MIC具有如下性質：(1)MIC是互信息歸一化后的最大值，因此MIC取值范圍在[0,1]之間；(2)由于互信息具有對稱性，因此，MIC(X,Y)=MIC(Y,X)；(3)I{x,y}的取值僅依賴于數據點的排序分布，對隨機變量進行單調變換，其數據點的排序分布不會發生變化，故MIC在隨機變量的單調變換下具有不變性；(4)大數據樣本下，對于無噪音的相關關系，MIC趨近于1；當兩個變量獨立時，MIC趨近于0。

在大數據相關分析方法中，MIC最具有代表性，發展最快，認同度最高，因此，本文將MIC作為大數據相關分析方法的典型代表與傳統相關分析方法進行比較。

二、適用范圍比較

表1 適用范圍比較

注：*表示該方法對變量的維度沒有限制。

比較可知：分布要求方面，Pearson相關系數、典型相關分析要求變量服從正態分布，其他方法則沒有此要求；測度的相關關系類型方面，Pearson相關系數和經典的典型相關系數只能度量隨機向量間的線性相關關系；Copula函數、HHG、MIC可以測度線性相關，也可以測度非線性相關；測度維度方面，典型相關分析、Copula函數、HHG可以測度多維數據相關性。

適用范圍的綜合比較來看，MIC對于兩維數據之間的相關關系顯現出明顯優勢，對隨機變量的分布沒有要求，測度的相關關系類型涵蓋了線性相關和非線性相關，缺點是不能測度多維數據的相關程度。

三、測度效果比較

(一)對非線性相關關系的測度

取X={xi:i=1:500}～U(-1,1)，按照表2-4中的各個相關關系類型模擬變量Y，計算變量X與Y之間的Pearson相關系數與MIC得分。

表2 MIC與Pearson相關系數對比表

結果表明，MIC可以準確度量變量之間的線性關系以及非線性關系，而Pearson相關系數則僅能識別線性相關關系。

(二)對異常值的敏感程度

取X={xi:i=1:30}～U(0,1)，ε={εi:i=1:30}～N(0,1),Y=2X+ε。在模擬得到數據(X,Y)基礎上增加四個離群點，增加離群點后的數據設為(X′,Y′)。左圖為數據(X,Y)的散點圖，增加離群點后，得到右圖，為數據(X′,Y′)的散點圖。

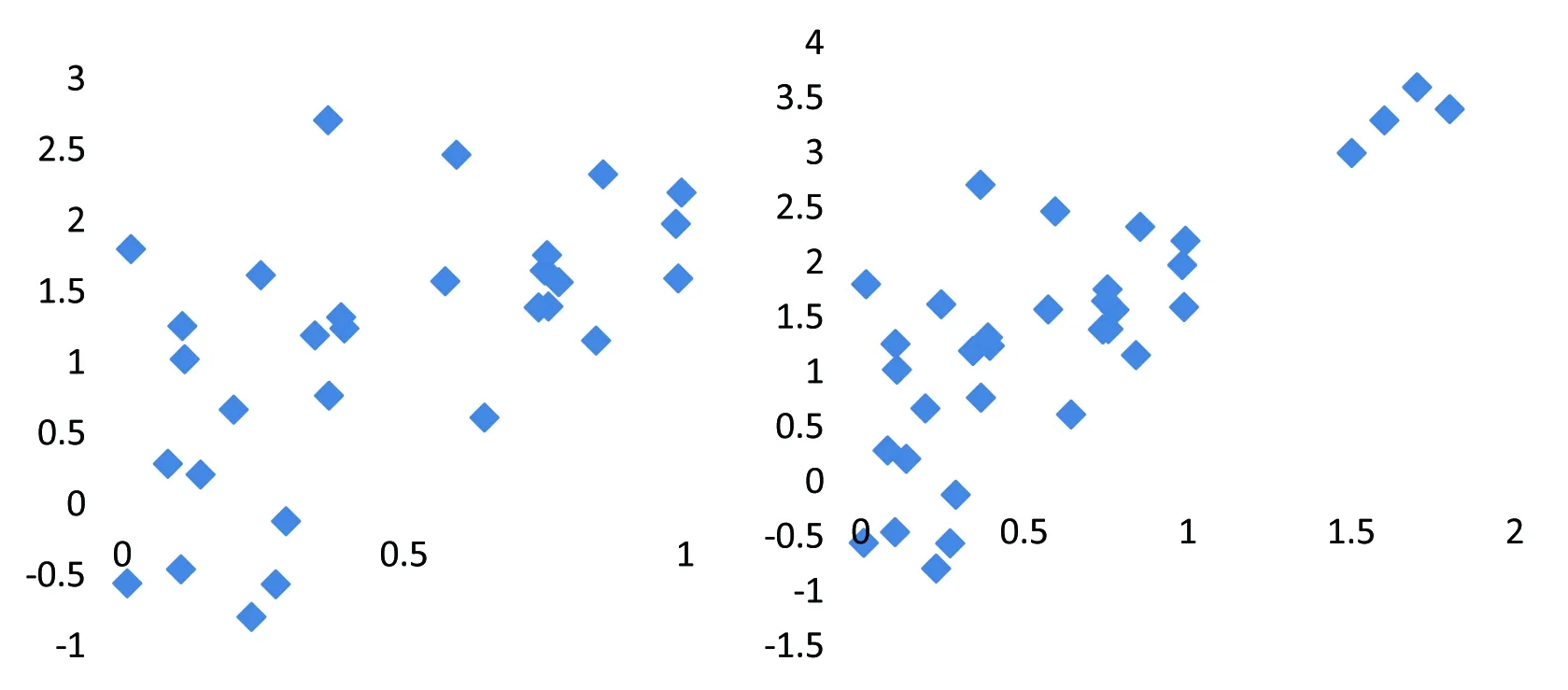
圖1 MIC穩定性示意圖

分別計算(X,Y)和(X′,Y′)的Pearson相關系數與MIC值，MIC(X,Y)=0.26，ρ(X,Y)=0.33；MIC(X′,Y′)=0.26，ρ(X′,Y′)=0.60。去掉離群點前后數據的MIC得分相同，而ρ(X′,Y′)-ρ(X,Y)=0.27，表明MIC具有穩定性，而Pearson相關系數易受異常值的影響。

四、相關關系的解釋能力比較

Copula函數、HHG、MIC三者均可以度量變量之間的非線性相關關系，除HHG方法之外，Copula函數和MIC都可以對相關關系進行進一步的描述和解釋。Copula函數能夠刻畫不同邊緣分布之間的連接結構，因此能夠全面地描述相關關系結構，在金融時間序列中被廣泛使用。而MIC方法則衍生出諸多統計量，可以通過這些統計量對變量之間的相關關系類型做出逐步推斷。例如：MIC-ρ2可以檢驗變量之間的相關關系類型是否為非線性相關關系，最大非對稱得分(maximal asymmetry score，MAS)用來度量兩個變量間的單調性，最大值(maximum edge value，MEV)可以用來判斷變量間的關系是否是函數關系，最小網格單元數(minimum cell number，MCN)可以用來衡量相關性的復雜程度。

五、計算速度比較

研究對象從樣本到類總體的轉變，對相關分析方法的計算能力與計算速度提出了較高要求，將MIC與HHG相關關系計算方法相比較，MIC的計算時間較短，滿足數據流挖掘中算法時間復雜度低的原則。

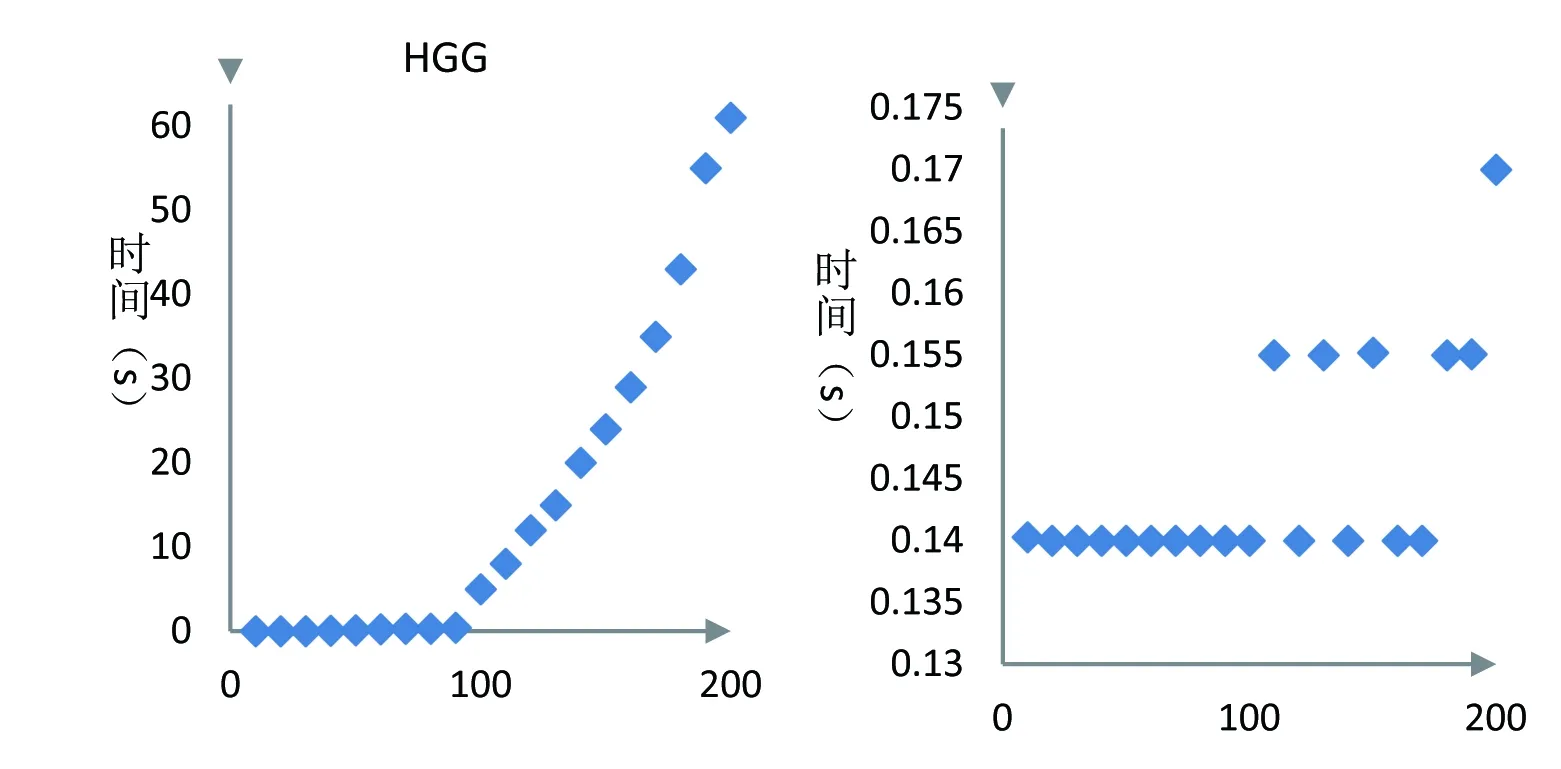
圖2 HHG與MIC計算時長比較

六、結論

通過比較研究發現，MIC具有以下優點：對于兩維數據的復雜相關關系測度適用范圍廣、結果測度準確，不易受異常值影響、解釋能力強、計算快，能夠滿足大數據挖掘需求；缺點方面：MIC只能測度兩變量之間的相關關系，不能測度多變量的相關關系，因此，對MIC方法的改進可以從測度變量的個數入手。