基于回歸分析的任務定價規律研究

趙希旺

（泰州學院船舶與機電工程學院，江蘇 泰州 225300）

一、模型的建立

對于研究任務定價規律問題，需要找出與定價相關的因素，首先需要判斷經緯度（地理位置）與任務定價是否相關，因此本文建立多元線性回歸模型，下面是建立多元線性回歸模型判斷項目定價與經緯度之間的聯系。

多元模型的矩陣表達式：

二、模型的求解

利用spss軟件對多元回歸模型進行求解，任務經緯度（地理位置）與任務定價關聯度大小求解結果如下表所示：

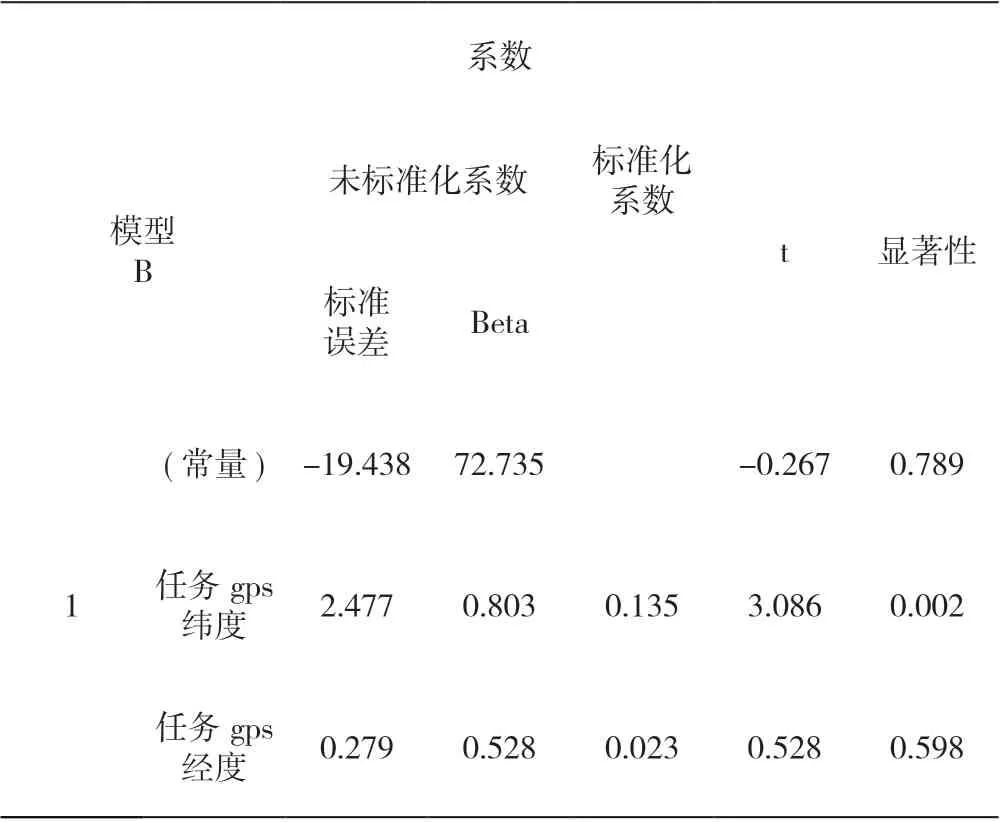
表1 地理位置與任務定價關聯度大小求解結果

任務經緯度的t的絕對值都明顯的大于0，從而可以判斷任務的經緯度與任務定價關系顯著。進而畫出會員分布和價格大小的對比圖如下。

圖1 會員分布和價格大小的對比圖

（橫坐標表示經度，縱坐標緯度和標價）

從圖中可以總結出的規律有：

（一）任務定價在地圖上呈現出價格有多個中心點并以中心點向四周價格遞減的規律。

（二）會員密集高的地方，項目定價較低，會員密集度低的地方，項目定價較高。

三、任務未完成原因分析

本文用邏輯回歸分類模型推斷任務未完成的原因，邏輯回歸的公式如下所示：

邏輯回歸函數是一個s形曲線，它的取值在[0,1]之間，在遠離0的地方函數值會很快接近0或1，這個性質使我們能夠以概率的方式來解釋。用spss軟件對任務定價與任務未完成情況進行邏輯回歸分析，分析結果如下表所示：

表2 模型摘要

結果分析：

（一）公式值為正時，對數似然值越高說明參數擬合效度越大，公式值為負時，絕對值越小參數擬合度越高。結合本題公式值為正，因而水面參數擬合效度高

（二）瓦爾德檢驗：瓦爾德是一個統計量，用于檢驗自變量對因變量是否有影響的，瓦爾德值越大，影響越顯著。