基于SVM的RBF網絡在農機總動力預測中的應用
吳志輝,王福林,董志貴
(東北農業大學 工程學院,哈爾濱 150030)
0 引言
農機總動力水平是農業機械化水平的重要指標,也是政府部門指定農業機械化發展規劃的重要依據,因此對農機總動力的預測具有重要意義。目前,關于農機總動力的預測有多種方法:人工神經網絡的效果較好,但大多數研究都是與BP神經網絡有關的[1-3];徑向基函數(Radial Basis Function,RBF)神經網絡[4]結構簡單、學習速度快。其核心思想就是在低維空間非線性相關關系通過基函數映射到高維空間后可能成為線性相關的,這樣就可以用線性方法解決原問題。在RBF神經網絡中,確定基函數中心的數量、位置以及寬度是RBF神經網絡的關鍵[5]。因此,人們一直試圖將各種高效的聚類算法應用在計算RBF神經網絡的基函數中心的過程中,最常用的一種做法是采用k-means聚類法來確定基函數中心,但需要預先設定希望得到的聚類數,這在復雜的實際情況中是很難做到的。針對K-means聚類的不足[6],潘琪等人提出利用系統聚類的方法來確定基函數的中心的方法,但系統聚類和K-means在本質上都是貪心算法的一種,也就具有了貪心算法的缺點,算法在每一步所做的決策對當前狀態來說都是最優的,這樣得到的最終解很可能不是全局最優解,且系統聚類法受異常值的影響較大[7],算法結構不穩定。為此,提出了一種支持向量機聚類來確定基函數中心的方法,具有很強的普適性和魯棒性,彌補了K-means和系統聚類在確定RBF神經網絡基函數中心過程中的不足,且把改進的RBF神經網絡應用到黑龍江省農機總動力的預測中,得到了很好的效果。
1 RBF神經網絡基本原理
RBF神經的結構如圖1所示。
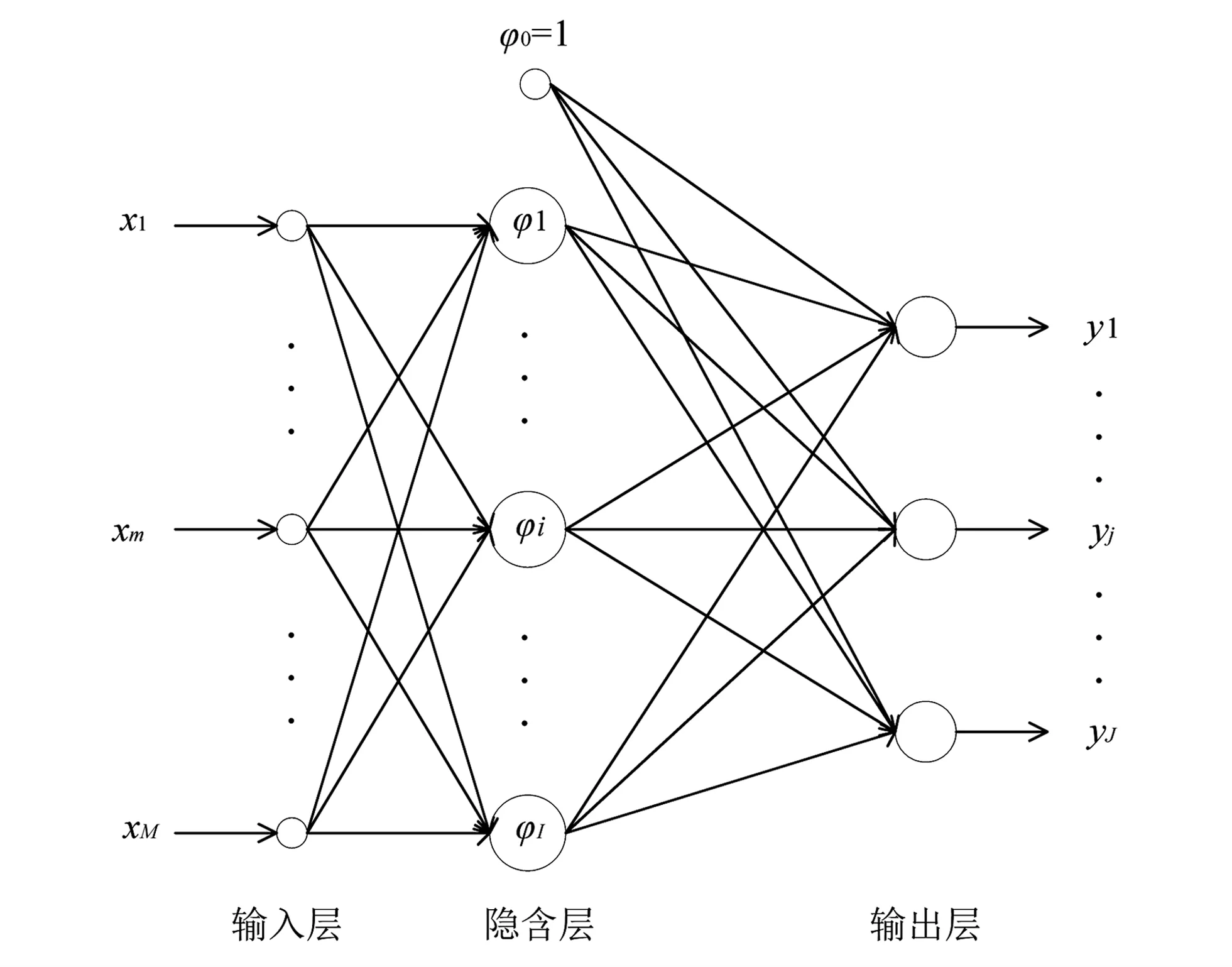
圖1 RBF神經網絡結構圖Fig.1 RBF neural network structure
第1層為輸入層,用來接收外界信號;中間層為隱含層,將輸入信號進行非線性轉換;第3層為輸出層,將對輸入信號的響應傳遞出去。
該網絡輸入層的神經元個數為n,隱含層神經元的個數為h,輸出神經元的個數為m。設RBF網絡的第i個輸入向量為Xi=[x1,x2,…,xn],基函數中心為[C1,C2,…,Cj,…,Ch]T,且有Cj=[c1,c2,…,cn],即每一個基函數中心的維度要與輸入向量的維度相同,b=[b1,b2,…,bm]T為閾值。隱含層與輸出層之間的非線性映射為φ(‖Xi-Cj‖),則第i個輸入的輸出為
(1)
令w0=-1,φ0=b,則有
(2)
設輸入向量的個數為P,則有
(3)
令φij=φ(‖Xi-Cj‖),i=1,2,…,p;j=1,2,…,m,那么可將上述方程組改寫為
(4)
進一步可以表示成
ΦW=D
(5)
其中,Φ為映射矩陣;W為系數矩陣;D為輸出矩陣。
RBF思想的核心是核方法的思想:低維空間的非線性相關關系經過核函數映射到高維數據空間很可能成為線性相關的。在映射過程中,離基函數中心的距離越近的位置對響應的影響越大。在RBF神經網絡中,基函的寬度就是基函數的探測區間,基函數的數量就是隱層節點的數量。RBF神經網絡的構造過程就是確定基函數中心及連接權值的過程,確定基函數中心需要考慮中心的數量、位置及寬度等幾方面。
2 基于SVM的RBF神經網絡學習算法
一般來講,RBF神經網絡的構建有兩個階段:首先,利用某種聚類方法把樣本集合劃分為h類,將每個類的中心作為RBF基函數的中心;其次,根據聚類結果確定和基函數中心相關的參數,并確定隱含層與輸出層之間的權值。從RBF的原理可以看出:基函數的中心及其相關的參數是設計RBF網絡的關鍵。針對傳統聚類方法的不足,本文提出利用支持向量機(SVM)來確定基函數的中心。
SVM與其他機器學習方法不同,過去的機器學習方法大多都是基于經驗風險最小化原則(ERM),而SVM是一種基于結構風險最小化(SRM)原則的學習算法;而基于SVM的聚類方法繼承了SVM算法的所有優點。
本文中,使用高斯核函數將數據點從數據空間映射到高維特征空間。在特征空間中,尋找包圍同類所有樣本的最小球體,這個球體被映射回原數據空間,在那里它形成一個圍繞數據點的輪廓,這些輪廓稱為聚類邊界,每個單獨輪廓所包含的點就屬于同一類別。隨著高斯核的寬度減小,數據空間中斷開的輪廓的數量增加,此時分類的數量就越多。同時,該方法還可以通過采用松弛變量(SVM中的軟間隔常數)來處理異常值[8]。
接下來,詳細介紹支持向量機聚類算法:
設{xi}?X是N個實例點的數據集,X?Rd為原數據空間。使用從X到某些高維特征空間的非線性變換φ,尋找半徑為R的最小包圍球體。由以下約束條件來描述,即
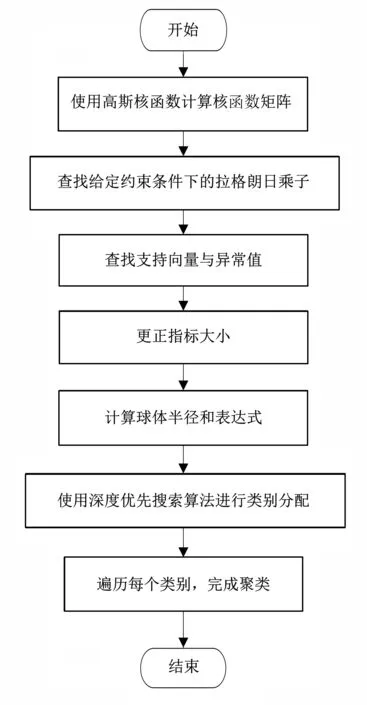
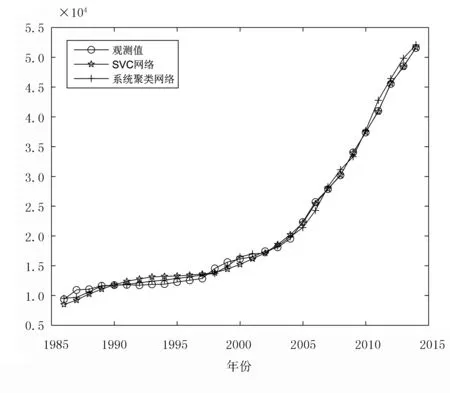
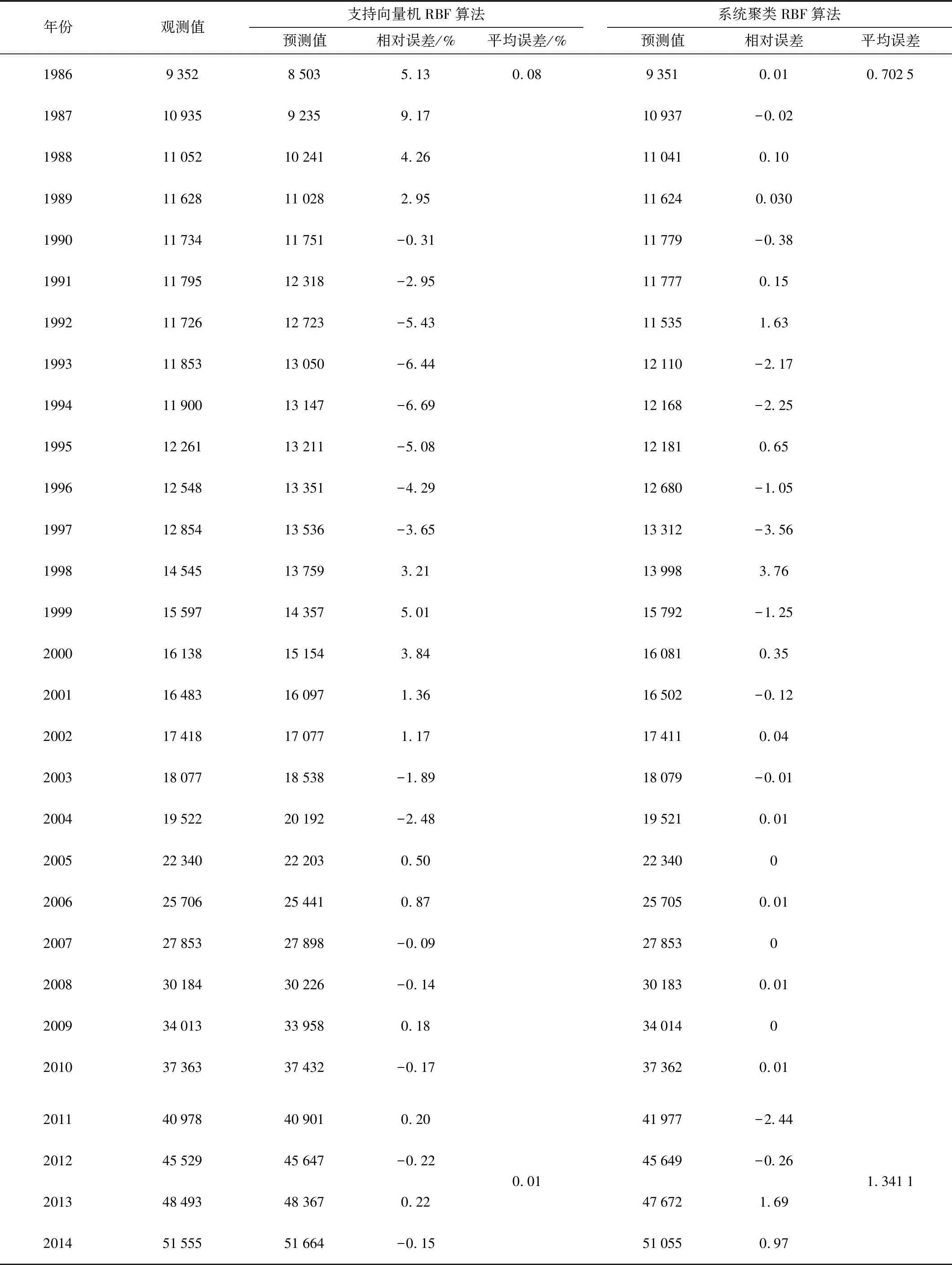
‖Φ(xj)-a‖2 (6) 其中,‖·‖為歐幾里得范數;a是球體的球心。通過加入松弛變量ξj來結合SVM中的軟間隔,則 ‖Φ(xj)-a‖2 (7) 其中,ξj≥0。為了解決這個問題,引入拉格朗日乘數,即 (8) 其中,βj≥0和μj≥0是拉格朗日乘子;C是一個懲罰因子,可以平衡球半徑和松弛因子比重,通常取[0-1];Cξj是一個懲罰項。 將L分別對R、a和ξj求導得 (9) (10) (11) 由KKT互補條件可得 ξjμj=0 (12) (13) 下面根據方程式(13)進行如下討論: 1)ξi>0且βi>0,由式(12)得此時μi=0,點xi位于特征空間球體的外部;又因為βj=C,所以該點對構造超球體有影響,此時,這個點被稱為受限支持向量(BSV)。 2)ξi>0且βi>0,此時μi>0,且‖Φ(xj)-a‖2=R2成立,所以對應的xi位于高維特征空間的超球體表面,又因0<βi 3)若βi=0,對應的xi位于高維特征空間的超球體內部,這樣的樣本點稱為內點,它們對于構造超球體或者支持函數并不起任何作用。 利用以上這些關系,可以消除變量R、a和μj,將拉格朗日變成對偶形式,它是變量βj的函數,即 (14) 由于變量μj不出現在拉格朗日函數中,可以用以下約束代替,即 0≤βj≤C,(j=1,…,N) (15) 加入核函數后的拉格朗日W,寫成 (16) 本文的核函數選擇高斯核函數,則 K(xi,xj)=e-q‖xi-xj‖2 (17) 其中,q為寬度參數。 義特征空間中樣本點x距球體中心的距離為 R2(x)=‖Φ(x)-a‖2 (18) 鑒于式(10)和核函數的定義,有 (19) 高維特征空間球的半徑為 R={R(xi)|xi是支持向量} (20) 則邊界輪廓上的點可以由如下集合定義,即 {x|R(x)=R} (21) 由式(20)可得:支持向量位于類邊界上,受限支持向量(BSV)位于類的外部,其它點位于類內。 接下來需要確定每個樣本在高維特征空間的類標號,本文采用構造完全圖的類別標定方法。具體算法如下: 1)計算特征空間中球體內或球體上的點對xi和xj之間的鄰接矩陣Aij,它的元素取值規則如式(22)。其中,i,j=1,…,N。采樣方法為隨機采樣,為了提高算法的速度,一般連續采樣10~20個,則 (22) 2)計算Aij對應數據集的聯通狀態,每個連通分量代表一個類別,采用深度優先算法遍歷全部樣本,確定每個類別的標號。 3)由于受限支持向量在超球體的外部,因此無法通過以上方式確定它們的類別標號,本文把它們標記為未分類狀態。 在構造最優超平面時,決策函數可以看成是支持向量關于核函數的展開式,因而算法的復雜度只與支持向量的個數有關,而與特征空間的維數無關。 數據空間中封閉輪廓的形狀由兩個參數決定:高斯核的尺度參數q和懲罰因子C。 關于這兩個參數選取的問題,一直沒有一套全面而系統的理論作為指導,這也一直是支持向量機聚類的一個研究方向,目前在實際應用中多采用經驗法或實驗法。 由前面的分析可知:在實際操作中,必須要考慮受限支持向量的個數。輪廓分裂點由參數C控制。從式(9)和式(15)可得 (23) 其中,nbsv是BSV的數量。因此,1 /(NC)是BSV數量的下限,設 (24) 當樣本數量N比較大時,異常值的比例傾向于p。即當存在不同的類別時,異常值(如由于噪聲)會阻止輪廓分離,所以使用受限支持向量(BSV)是非常有用的。由式(23)可得,當C值越小時得到的BSV數量越多。 下面利用支持向量機聚類的方法計算基函數的中心,構造一個RBF神經網絡。假設網絡的輸入樣本為X=[X1,X2,…,Xk,…,Xn]T,任意一個訓練樣本為Xk=[xk1,xk2,…,xkm,…,xkM],k=1,2,…,N。其中,xkm表示第k個樣本的第m個輸入,RBF神經網絡所對應的網絡實際輸出為Yk=[yk1,yk2,…,ykj,…,ykJ],k=1,2,…,N。 根據得到的基函數中心計算徑向基函數的寬度:設其它聚類中心到與第i個聚類中心距離的最小值di,即di=min(‖Ci-Cj‖),按照公式σi=λdi計算各基函數的寬度σi。其中,σ稱作重疊系數,用來控制各個徑向基函數的平滑程度,重疊系數的值越大,基函數的圖像就越平滑。 用梯度法確定RBF神經網絡隱含層與輸出層之間的權值,其具體實現過程如下: 1)計算核函數矩陣,使用高斯核函數; 2)查找給定約束條件下的拉格朗日乘數、支持向量與異常值,并更正受限支持向量與支持向量的值; 3)計算球體的表達式,采用深度優先搜索算法對對每一個樣本點進行類別分配; 4)根據SVM的聚類結果計算每個聚類中心并把它作為每個基函數中心; 5)計算各基函數的寬度σi; 6)訓練RBF神經網絡,得到網絡隱含層與輸出層之間的權值。網絡權值的計算可以選擇代數方法,也可以采用監督訓練法,本文采用監督訓練法。支持向量聚類的流程圖如圖2所示。 圖2 支持向量聚類流程圖Fig.2 Flow chart of clustering based on SVM 基于支持向量機聚類的RBF神經網絡的流程圖,如圖3所示。 圖3 基于SVC的RBF神經網絡的流程圖Fig.3 Flow chart of RBF neural network based on SVC 針對一般神經網絡在非線性時間序列預測問題中收斂速度慢的問題,使用基于支持向量機確定基函數中心的方法來改進徑向基神經網絡實現的動態的建模與預測,并使用該方法對一系列非線性時間序列進行仿真預測。 為了驗證改進算法在非線性時間序列預測中的準確性,本部分對黑龍江省1980-2014年的農機總動力進行非線性時間序列預測,并與系統聚類法構建的神經網絡的預測結果進行對比。黑龍江省這35年的農機總動力數據如表1所示[9]。 為了避免不同量綱對訓練網絡的影響,需要對數據進行標準化處理,把原始數據映射到區間[0.2,0.8]上,按照式(25)進行數據的標準化工作。則 (25) 其中,xmin為數據中的最小值;xmax為數據中的最大值。 表1 黑龍江省1980-2014年農機總動力Table 1 The total power of agricultural machinery in Heilongjiang Province from 1980 to 2014 構建訓練集數據,假設有M個樣本,每個樣本的維度為M-N,則一共可以構建N個時間序列。初始化輸入維度為6,即以連續6年的實例作為一個輸入,第7年的實例作為輸出值。按照這種方式構建時間序列,共可以構成35-6=29組數據。選取前25組數據作為訓練集,指定后4組數據為測集,讓它們與網絡的預測效果進行比較。 分別用改進算法和系統聚類的方法訓練神經網絡,用其預測2011-2014年黑龍江省的農機總動力,然后將預測值與實際值進行比較。預先徑向基神經網絡的初始參數如下:輸入神經元個數為6,輸出神經元個數為1,初始權值W0=[1,1,…,1]T,初始閾值b0=1,網絡學習精度0.001,重疊系數ε=1,學習率是0.1,支持向量機聚類時的C=1,q=300。采用系統聚類訓練徑向基神經網絡時,網絡的各項參數均與改進方法相同。網絡的觀測值和實際輸出值的曲線對比圖如圖4所示,兩種方法具體的輸出情況如表2所示。 圖4 黑龍江省1986-2014年農機總動力趨勢圖Fig.4 Trend of agricultural machinery total power in heilongjiang province from 1986 to 2014 表2 實驗結果Table 2 Experimental results Table 提出了用支持向量機聚類來確定徑向基函數中心的新方法,并給出了這種方法的計算方法及相關模型。將這種方法與系統聚類方法進行對比,分析給出了這種方法的優越性。該方法也不需要預先給出基函數中心的初始點,也不需要預先確定徑向基函數的個數,有效提高了神經網絡的穩定性和泛化性。通過實驗驗證了改進的神經網絡在提高網絡穩定性和提高預測精度等方面的性能。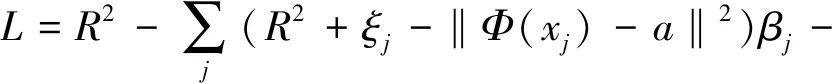
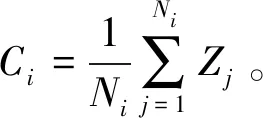
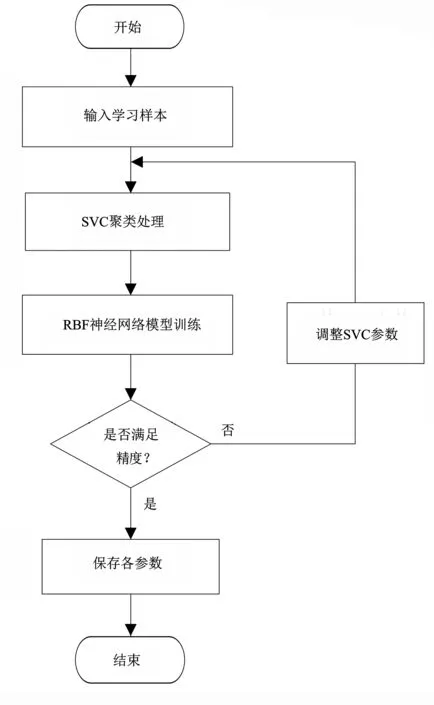
3 農機總動力預測實驗

4 結論

