基于PSO算法的木薯收獲機拔起速度控制系統參數優化
王錦濤,楊 望,楊 堅,鄭 賢,戚鵬偉
(廣西大學 機械工程學院,南寧 530004)
0 引言
拔起速度可控的木薯收獲機控制器是一個使用PID控制的閉環系統,主要通過閥控液壓馬達系統進行調控,使液壓馬達的輸出轉速換算為拔起機構豎直方向的速度,盡可能地擬合較優拔起速度,從而達到高效率、低損失的目的,關鍵是控制參數的尋優。而采用目前的閉環系統控制器控制參數的調試、尋優方法,進行參數尋優,耗時費力。因此,本文采用PSO算法,通過建立液壓系統數學模型,開展木薯收獲機PID控制參數的尋優調試方法研究,以提高其參數尋優速度,滿足木薯收獲機控制器的要求,為控制器的參數調試和優化提供新的思路和方法。
1 木薯收獲機結構及工作原理
木薯收獲機工作系統主要由機械系統、電氣控制器,以及液壓系統構成。木薯收獲機的整體結構如圖1所示。
木薯收獲機以拖拉機為動力,液壓機構使用拖拉機自帶的液壓泵作為動力源。作業時,前置的松土鏟松土,隨著木薯收獲機向前移動;當木薯莖稈觸碰到夾持機構上的觸碰傳感器時,控制器電磁單向閥通電,液壓油流向液壓機構,二位四通換向閥通電,液壓油換向,夾持機構夾持莖稈;當夾持壓力達到設定值后,輸出控制信號,控制伺服比例閥,液壓馬達轉動,帶動齒輪齒條工作,夾持機構沿導軌向上運動,將木薯塊根拔起;當夾持機構運動到最高點,觸發限位傳感器時,伺服比例閥使液壓馬達反轉,滑塊等機構復位,同時二位四通換向閥失電,夾持機構松開,完成一次拔起作業[1]。
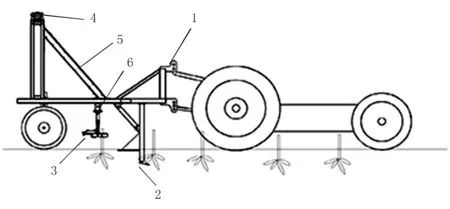
1.懸掛裝置 2.松土鏟 3.夾持裝置 4.液壓馬達 5.拔起裝置 6.土薯分離裝置圖1 木薯收獲機示意圖Fig.1 Sketch of cassava machine
2 液壓系統數學模型
木薯收獲機液壓系統工作流程圖,如圖2所示。
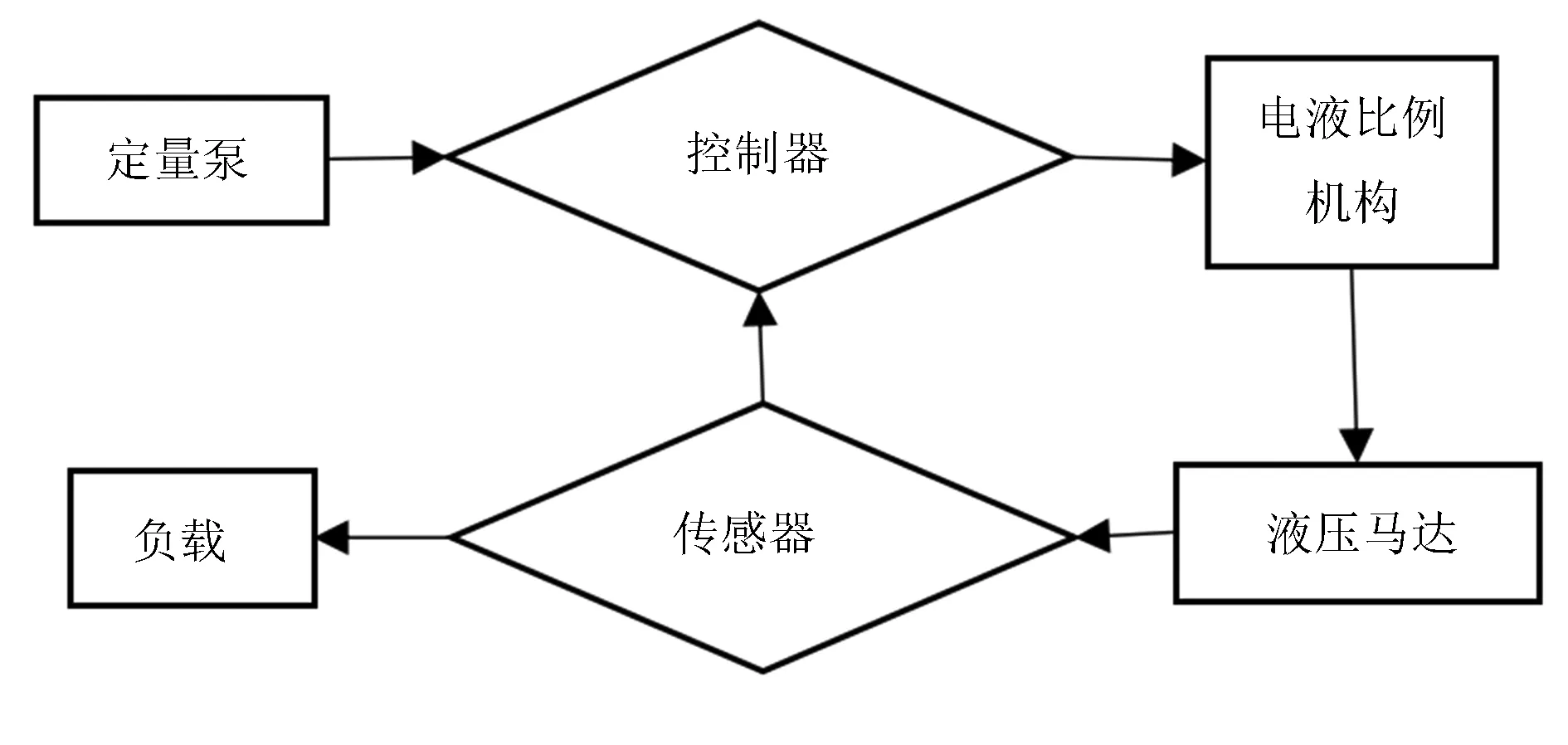
圖2 液壓系統工作流程圖Fig.2 hydraulic system work flow chart
由于木薯收獲機的液壓系統由力士樂4WRE6型伺服閥對BMR50液壓馬達進行控制,參考文獻[2-3],得液壓馬達輸出角速度與外負載及輸入電壓間的傳遞函數為
(1)
(2)
其中,Dm為液壓馬達排量;Kq為控制閥輸出液壓油流量與輸入電流之比;K電為伺服閥的電壓輸入信號與馬達轉速之間的增益;βe為液壓油的彈性模量;ωh為液壓的固有頻率;ξh為液壓的阻尼系數;V為液壓馬達和管道總容積。液壓系統基本參數值如表1所示。
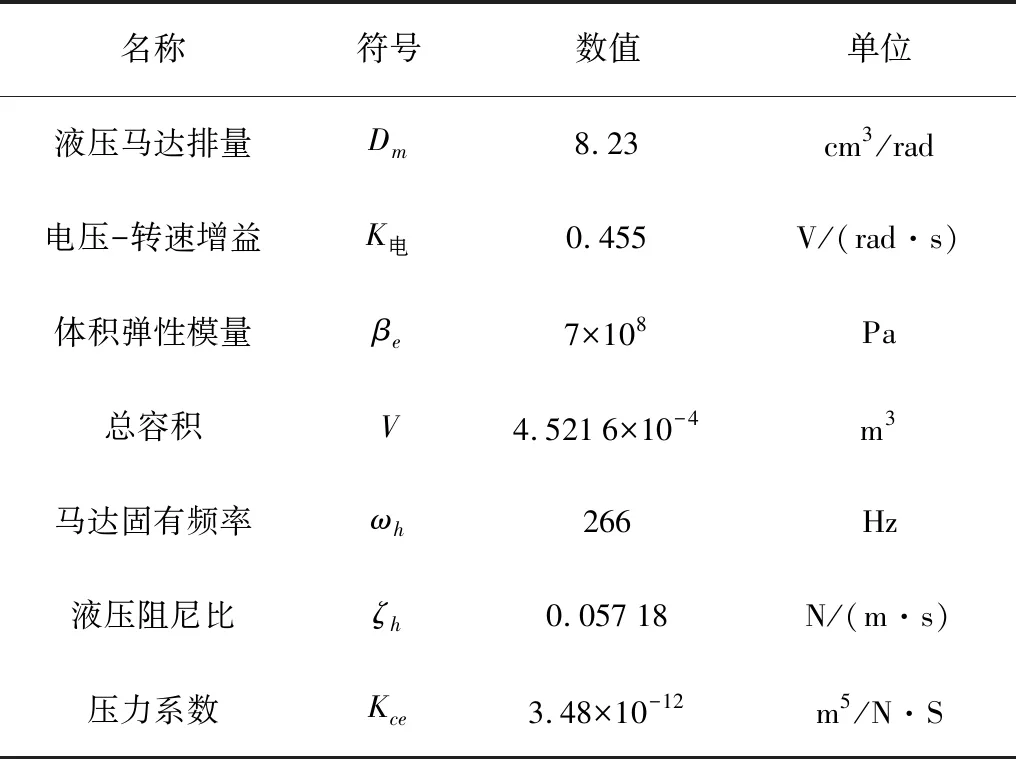
表1 液壓系統各參數計算Table 1 Calculation of hydraulic system parameters
將表1參數代入式(1)和式(2)得閥控液壓馬達調速系統的傳遞函數為
(3)
3 控制器參數優化
3.1 控制目標
由文獻[4]的研究可知,木薯塊根拔起的較優速度模型為
(4)
其中,t為時間。式(4)中的正弦部分,由安裝在木薯收獲機上的抖動機構提供,因此將式(4)中正弦部分去掉,只將拋物線函數作為木薯塊根拔起的較優速度模型[5-6]。因此,控制液壓馬達的目標是使夾持機構隨滑塊豎直方向的運動速度與式(5)相一致,即
V(t)=-0.056t2+0.521t+0.048
(5)
3.2 控制器參數優化
3.2.1 PSO算法
1995年,James.Kennedy和Russell.Eberthart提出了PSO算法,該算法模擬鳥群覓食行為進行計算。在應用中,將每個問題的解看做一個粒子,在尋求最優解的過程中,所有的粒子都在一個D維空間中進行搜索;每個粒子有一個適應度函數,用來確定在迭代運算過程中,判斷當前的位置的好壞;每個粒子具備記憶功能,記住所搜尋到的最佳位置;每個粒子具備一定的速度,用以決定其飛行距離和方向。該速度通過其本身飛行經驗及群體飛行經驗進行調整[6]。
假定:在D維空間中,有N個粒子,那么:粒子i的位置為xi=(xi1,xi2,…,xid);粒子i的速度為Vi=(Vi1,Vi2,…,Vid);粒子i經歷過最好的位置為pbesti=(Pi1,Pi2,…,Pid)。粒子群經歷過最好的位置為gbest=(G1,G2,…,GD)。另外,限定D為空間的空間位置以及粒子的速度,當速度超過(小于)最大(最小)限定速度時,該粒子設定為最大(最小)速度,當飛行超過邊界時,將粒子位置設定在邊界。
在t+1時刻,該粒子的位置更新公式[6]為
(7)
速度更新公式[6]為
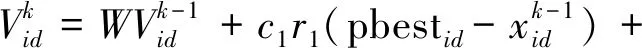
(8)
3.2.2 優化方案及驗證
利用PSO算法對PID控制參數進行優化,是對PID參數進行空間尋優,通過不斷將尋找到的參數數值代入PID算法,對控制對象進行控制測試,通過性能指標判斷當前參數的優劣[7]。通過不斷迭代,尋找最優參數,當性能指標達到要求后,算法停止,輸出尋找到的最優解[8]。本文主要采用MatLab軟件進行算法編寫,使用MatLab自帶的Simulink進行PID控制器的仿真,通過PSO算法,調用Simulink的PID控制器進行不斷迭代運算,每迭代一次,調用一次Simulink。利用PSO算法,對PID控制器進行參數優化整定,其設計流程如圖3所示。
本文選取一階時滯、二階時滯和三階時滯模型作為測試對象,為了檢驗PSO算法對復雜函數的尋優能力,增加了一種不穩定系統函數作為測試對象。本文采用ITAE作為性能指標,各測試對象如表2所示。
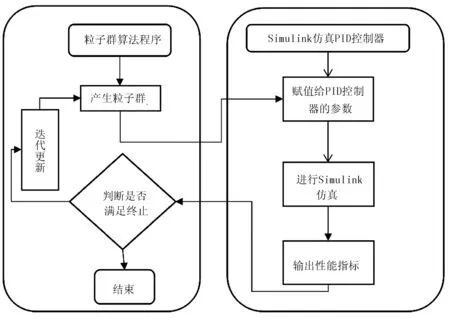
圖3 優化流程圖Fig.3 Optimization flowchart

表2 測試對象Table 2 Test objects
其中,ITAE為時間絕對偏差積分,即
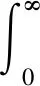
(9)
本文采用MatLab自帶的Simulink工具箱,建立控制模型,如圖4所示。
圖5~圖8中的(a)、(b)、(c)圖分別是各測試函數的Kp、Ki、Kd參數值的迭代曲線、適應值迭代曲線和Kp、Ki、Kd參數優化后的仿真曲線。
由圖6~圖9的(c)圖可知:采用PSO算法,進行PID參數優化,對于含有時滯環節的模型和不穩定系統模型,都能找出合理的參數,使控制器平穩輸出。
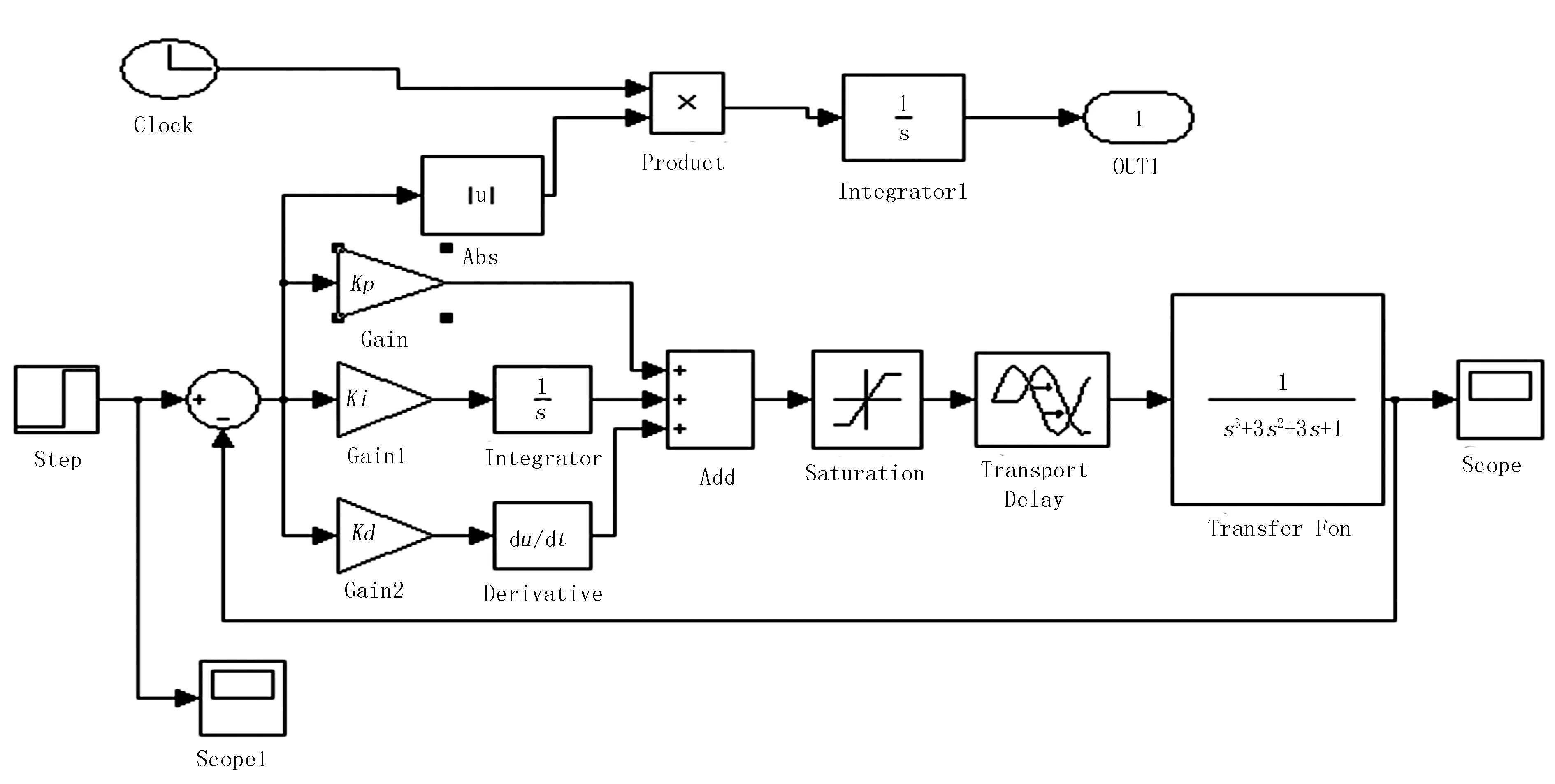
圖4 Simulink模型Fig.4 Simulink model
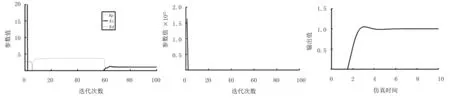
(a) 參數迭代曲線 (b) 適應值迭代曲線 (c) 仿真輸出曲線圖5 一階時滯系統測試模型曲線Fig.5 Curve of test model for first-order time-delay system
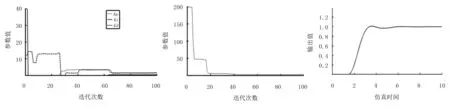
(a) 參數迭代曲線 (b) 適應值迭代曲線 (c) 仿真輸出曲線圖6 二階時滯系統測試模型曲線Fig.6 Test model curves for two order time-delay systems
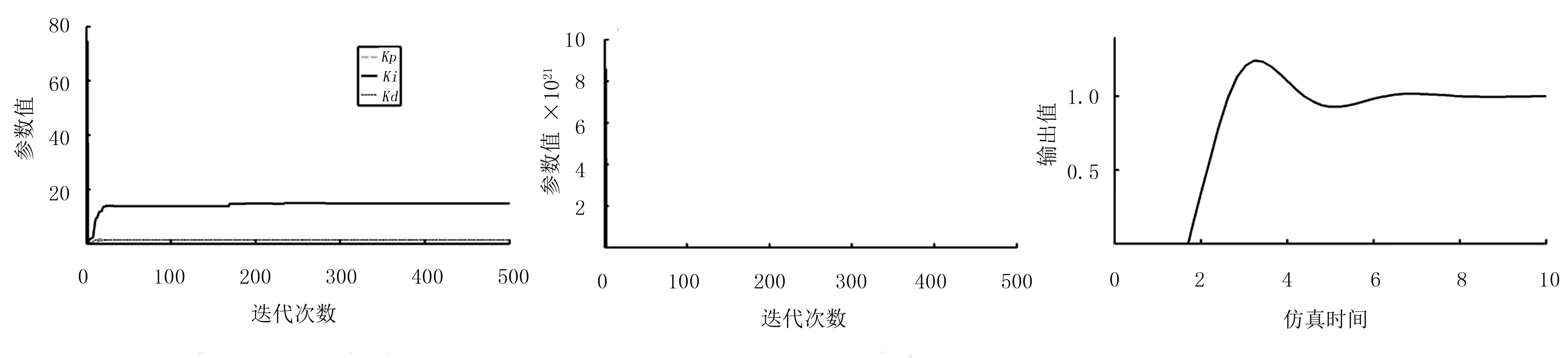
(a) 參數迭代曲線 (b) 適應值迭代曲線 (c) 仿真輸出曲線圖7 三階時滯系統測試模型曲線Fig.7 Test model curves for three order time-delay systems
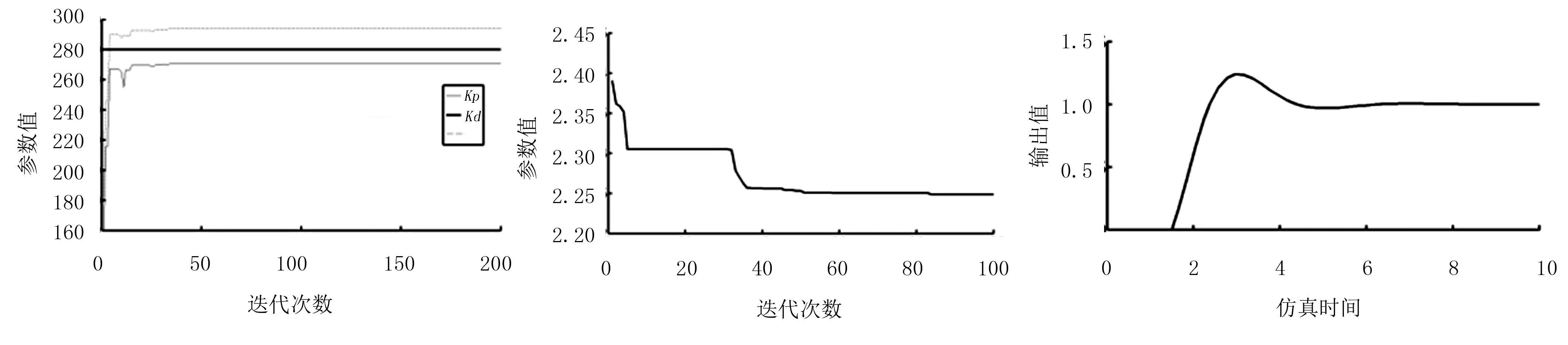
(a) 參數迭代曲線 (b) 適應值迭代曲線 (c) 仿真輸出曲線圖8 不穩定系統測試模型曲線Fig.8 Curve of an unstable system test model

(a) 參數迭代曲線 (b) 適應值迭代曲線 (c) 仿真輸出曲線圖9 傳遞函數模型迭代曲線Fig 9 Transfer function model iteration curve
將傳遞函數代入控制器模型中,使用PSO算法進行參數優化,得到的結果如圖9所示。最終,優化后Kp、Ki、Kd分別為0.644 1、2.726 9、0.036 2。采用階躍函數進行檢驗,優化后的控制器,超調量極小,如圖9中的(c)圖所示。將輸入信號換為較優速度方程,再次進行檢驗,其結果如10所示。
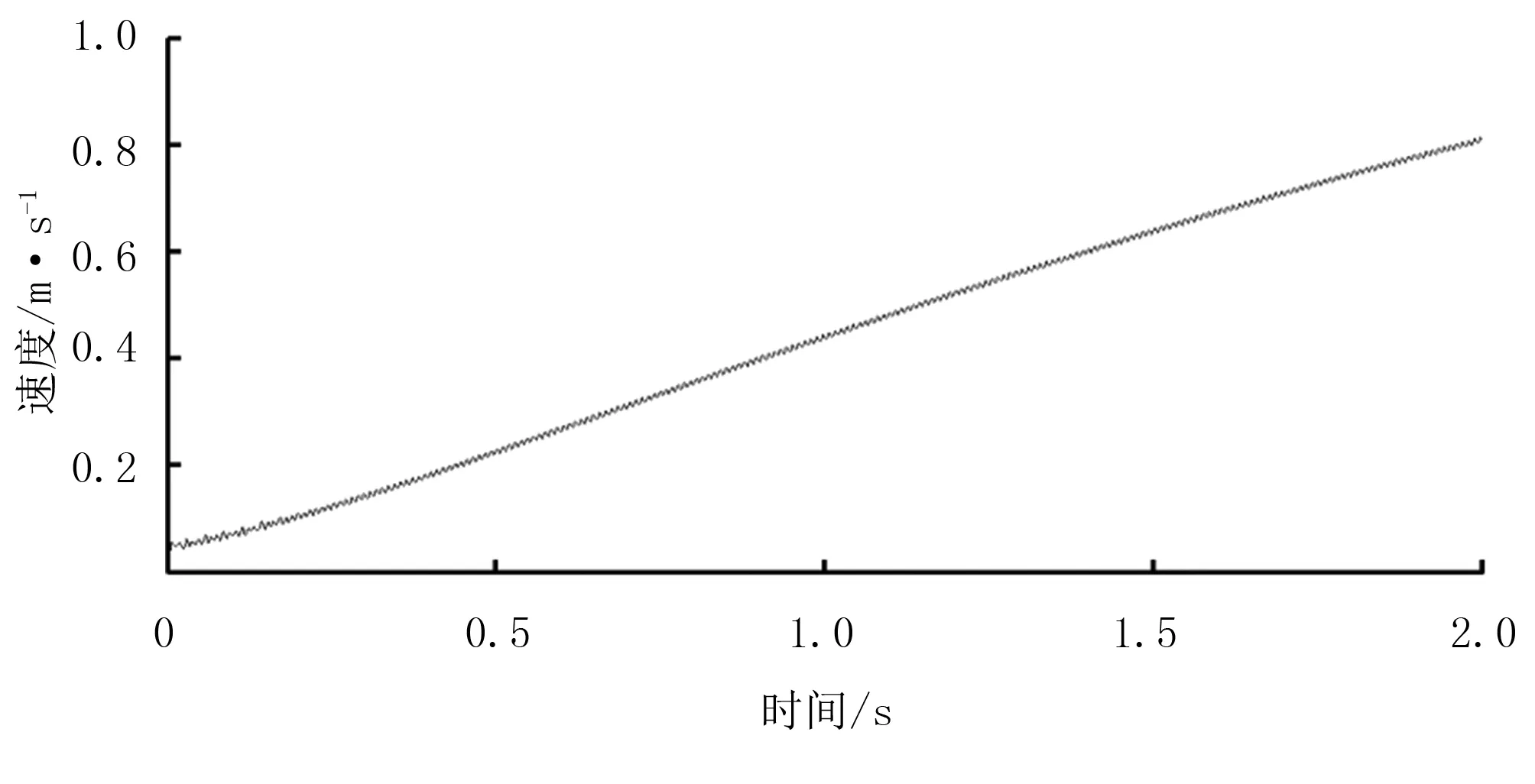
圖10 較優速度方程擬合結果Fig.10 Results of better velocity equation fitting
由圖10可知:優化后的控制器對于較優速度方程的擬合度良好。將輸出曲線放大后,發現曲線存在一定震蕩,這是由于仿真精度不夠,但精度增加后輸出曲線會進一步平滑。
4 田間試驗驗證
4.1 試驗方法
將木薯收獲機控制器分別置手動位和自動位進行收獲作業。對收獲過程中液壓馬達的輸出轉速進行采集,與最優速度方程進行比較,檢驗控制效果。試驗時,拖拉機行使用Ⅰ擋行進,速度為0.225m/s。
4.2 試驗設備和場地
試驗設備為木薯收獲機,雷沃504E拖拉機及筆記本電腦等,試驗場地為廣西大學木薯試驗田。 試驗現場如圖11所示。
4.3 結果分析
隨機選取4棵木薯,對其作業過程中液壓馬達輸出轉速進行采集。由于液壓馬達輸出轉速由編碼器進行采集,得到的是角速度,需要對其進行轉換,轉換為木薯收獲機滑塊的線速度。轉換后的速度與最優速度方程對比圖如圖12所示。

圖11 試驗現場Fig.11 Test site
通過對液壓馬達輸出速度曲線與標準速度曲線的對比發現:液壓馬達的輸出基本上能較好地擬合較優速度方程曲線。每棵木薯在收獲作業時,液壓馬達的前0.14s均無輸出,這是因為傳感器、控制器等有一定的反應時間;且由于伺服比例閥有一定的輸出死區,在前0.14s內,由于控制器輸出較小,處在伺服比例閥的死區范圍內,因此無輸出。
第1棵木薯在手動模式下進行收獲作業,除了剛開始作業時速度抖動較大,之后均能較好地擬合較優速度方程,輸出速度的誤差率為13.61%;除了開始的液壓無動作的0.14s外,整個工作過程速度誤差為3.74%。
從第2棵木薯開始,之后均為自動模式下,連續作業時采集到的數據。第2、3、4棵木薯在收獲時,控制器的控制效果比較理想。第2棵木薯在0.54~0.76s之間,木薯收獲機的輸出速度與較優速度方程之間偏差較大,輸出速度持續大于較速度。經過分析與實地考察后發現:由于在試驗田中進行測試時,試驗田不平整,有石塊等雜物存在,導致拖拉機前進阻力增大,拖拉機的發動機轉速短時間內迅速增大,拖拉機的齒輪泵輸出流量同時也增大;最終,由于液壓系統的輸入流量增大,使得液壓馬達在短時間內輸出速度偏離了最優速度。其輸出速度的誤差率為14.73%,除去前0.14s,整個作業過程,輸出速度的誤差率為4.99%。收獲第3棵木薯時,輸出速度的誤差率為14.39,除去前0.14s液壓系統無動作時間,整個作業過程誤差率為4.61%。第4棵木薯進行收獲時,輸出速度誤差率為14.10,除去前0.14s,誤差率為4.28%。
以上幾棵木薯收獲作業時,液壓馬達速度輸出誤差率平均為4.32%。經過分析可知,經過優化后的控制器其輸出誤差較小,且控制性能穩定。
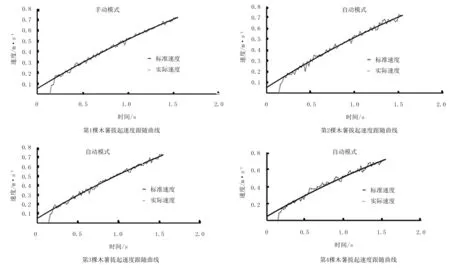
圖12 木薯拔起速度跟隨曲線Fig.12 The speed following curve of cassava pullout
5 結論
采用PSO算法,以液壓系統的傳遞函數為控制目標,通過調用由Simulink搭建的控制器模型,表明對控制器參數進行優化的方法可行,且便捷。對木薯收獲機的控制器的參數進行優化,得到控制的優化參數Kp、Ki、Kd分別為0.644 1、2.726 9、0.036 2。田間試驗表明:控制器控制效果良好,性能穩定。

