基于SPH法的船式拖拉機葉輪單輪葉驅動性能研究

張 超，孫 勇，周明剛，江 昱

(湖北工業大學 農業機械工程研究設計院，武漢 430068)

0 引言

船式拖拉機是我國特有的水田動力機械，其獨特的“浮滑式”工作原理使得葉輪的滾動阻力是船體滑行阻力的3～4倍，即作為行走驅動裝置—葉輪的功率損失大約占全部功率損失的75%～80%[1]。因此，葉輪結構參數對船式拖拉機的牽引效率具有很大影響。

國內外學者采取理論分析和實驗測試的方法對葉輪作業性能進行了大量研究。邵耀堅等[2-5]首先提出以葉輪作為機耕船驅動輪，并通過對單輪葉動力性能的研究，分析了輪葉傾角、下陷深度及滑轉率對輪葉驅動性能的影響，為驅動輪的設計提供了依據。Gee-Clough、Chancellor[6]通過實驗對土壤中單輪葉進行了測試，結果表明土壤含水率、輪葉形狀、下陷深度等參數對單輪葉受力具有較大影響。Hermawan等[7]使用自制土箱測試并分析了驅動輪與土壤作用過程中土壤對輪葉的反作用力。Fajardo等[8]在自制黏土試驗箱內進行了機耕船驅動輪試驗，研究了輪葉角和驅動輪轉速對驅動輪受力的影響。陸華忠、羅錫文[9]通過自制土槽實驗，分析了輪葉推進力、支撐力及驅動效率變化與土壤流動特性之間的關系。目前，關于輪葉與土壤相互作用的理論研究主要采用力學分析及經驗公式進行計算，分析過程存在很多簡化，與實際工況存在較大誤差。采用光滑粒子流體動力學法(SPH)可以從工程應用角度出發，細致全面地考慮葉輪結構、土壤參數及葉輪-土壤接觸特性，獲得更加準確可靠的結果。

為此，以課題組研制的HH709S型船式拖拉機葉輪的單輪葉為研究對象，基于SPH方法，對輪葉與土壤的作業過程進行動力學仿真，分析單輪葉結構參數對其驅動性能的影響，最終獲得驅動效果最佳的輪葉結構。

1 單輪葉-土壤SPH動力學仿真模型

光滑粒子流體動力學法(SPH)由Lucy、Gingold等[10-11]于1977年首次提出，基本思想是將連續介質離散為一系列具有質量的質點，通過跟蹤質點的運動軌跡，建立其動力學方程，最終獲得系統的力學特性。SPH是一種無網格法，常被用以解決有限元法在模擬如土壤切削、高速碰撞及爆破等動態大變形情況下出現的網格畸變問題[12-14]。

1.1 單輪葉有限元模型

本文在課題組前期研制的HH709S型船式拖拉機驅動葉輪基礎上展開的研究，如圖1所示。在一定滑轉率下，通過仿真模擬單輪葉與土壤的作用過程，對輪葉結構參數進行優化。在此，首先對船式拖拉機葉輪的單輪葉進行建模，原輪葉面傾角α=5°，軸向角度θ=30°，輪葉厚度b=8mm，輪葉長度L=250mm，輪葉寬度B=182mm，如圖2所示。輪葉模型單元類型采用Solid164實體單元，因輪葉剛度遠大于土壤剛度，為節省計算時間，將輪葉設置為剛體模型，其材料密度為7.8×103kg/m3，泊松比為0.27，彈性模量為2.1×1011Pa。

圖1 HH709S型船式拖拉機及葉輪Fig.1 HH709S boat-tractor and its driving wheel

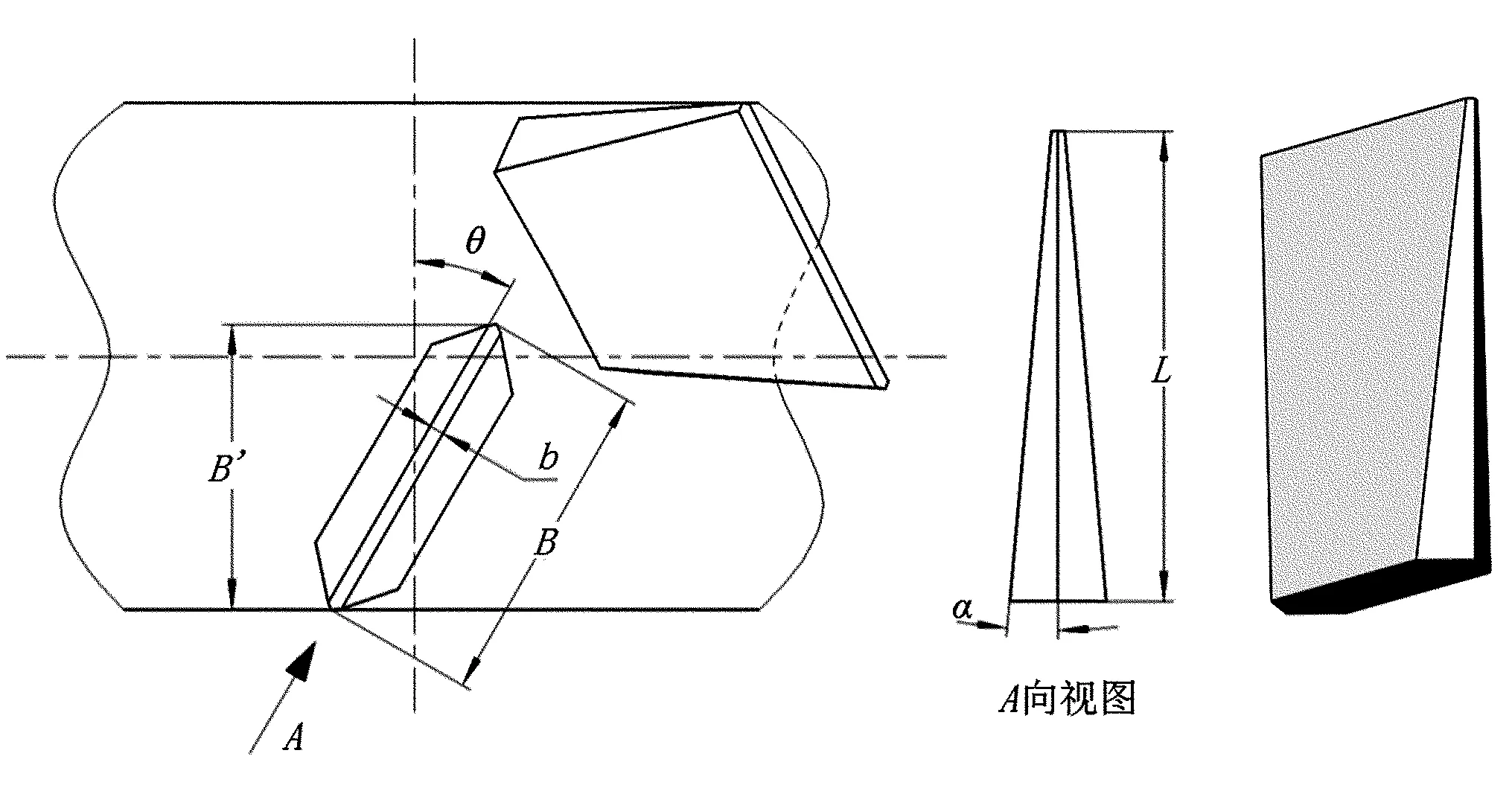
α.輪葉面傾角 θ.軸向角度 b.輪葉厚度 L.輪葉長度 B.輪葉寬度 B′.輪葉軸向相對寬度圖2 單輪葉結構示意圖Fig.2 Structure of the single lug

1.2 土壤SPH模型

土壤是一種三相材料，由土壤顆粒、孔隙氣和水組成，其參數多而復雜。土壤材料模型的選擇對仿真模擬的準確性影響很大，本文土壤模型采用土壤專用材料MAT147(MAT_FHWA_SOIL)。該材料考慮了土壤含水率、應力軟化和變形率等參數的影響[15]，對Mohr-Coulomb屈服準則屈服面進行了雙曲線擬合，擬合后的屈服面用公式表述為

(1)

式中F—屈服面力；

P—壓力；

φ—內摩擦角；

J2—應力偏張量的第二不變量；

K(θ)—偏應力面中的極角；

ahyp—修正系數；

c—內聚力。

土壤SPH模型由LS-DYNA專有的前后處理軟件LS-PREPOST建立，在滿足輪葉運動及邊界條件處理要求的前提下，建立長方體土體SPH模型，三維尺寸為900mm×480mm×430mm(長×寬×高)，SPH粒子數為185 760。參考文獻[16]中的水田土壤參數，本文選取的土壤主要參數如表1所示。

1.3 網格劃分與邊界條件施加

葉輪輪葉采用六面體網格單元劃分，其單元數為1 528。HH709S型船式拖拉機作業過程中滑轉率約為25%，依據實際工況，設置輪葉繞軸心轉速為1rad/s，水平方向前進速度為2.07m/s，輪葉最大入土深度為310.5mm。對土壤模型底面添加全約束，土壤側面添加對稱約束(SPH_SYMMETRY_PLANE)，輪葉與土壤SPH粒子之間采用自動點面接觸類型(AUTOMATIC_NODES_TO_SURFACE)，其靜摩擦因數為0.3，動摩擦因數為0.25[17]，總求解時間為0.6s。單輪葉-土壤動力學模型如圖3所示。

表1 水田土壤主要參數Table 1 Parameters of the paddy soil material

圖3 單輪葉-土壤SPH動力學模型Fig.3 Dynamic simulation model of the lug-soil

2 結果分析

在上述動力學模型基礎上，對單輪葉與土壤的相互作用進行求解計算，圖4(a)展示了作用過程中輪葉轉角ω分別為20°、45°、90°、100°時土壤內部應力分布云圖。在此過程中，任意時刻土壤對輪葉的作用力均可分解為水平推進力Fp和垂直支撐力FL，如圖4(b)所示。支撐力是輪葉滾動阻力產生的主要原因，因此在保證足夠推進力的前提下，減小支撐力FL的絕對值，可有效減小滑轉率，提高葉輪的驅動效率[9]。

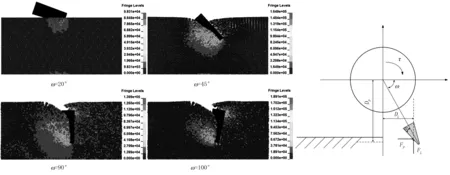
(a) 輪葉與土壤作用過程 (b) 輪葉受力分析圖4 單輪葉與土壤作用過程及受力分析Fig.4 Interaction between single lug and soil and the force on the lug

單輪葉與土壤相互作用的整個過程中，輪葉所受的水平推進力Fp和垂直支撐力FL如圖5所示。結合圖4(a)可以看出：輪葉入土后驅動面向后下方擠壓土壤，此時輪葉驅動面與水平面的夾角較小，支撐力FL快速增大，在轉角ω達到45°附近時達到最大值；隨著輪葉繼續運動，輪葉驅動面與水平面的夾角持續增大，FL開始迅速減小；當ω達到100°時，FL為0，繼而因挑土作用變為負值。推進力Fp在輪葉剛入土時為負值，這是由于輪葉水平夾角較小且其水平方向運動速度較大，而輪葉存在一定厚度，從而在水平方向產生推土作用。隨著ω增大，Fp持續增加，并在ω達到90°附近時達到最大值。然后隨著ω的增大逐漸減小，并在出土時由于非驅動面產生向前推土作用，所以為負值。仿真結果與文獻[9]實驗研究結果趨勢吻合，驗證了模型的有效性。另外，本文還分別研究了輪葉驅動面傾角α、軸向角度θ、輪刺厚度b等參數對輪葉驅動性能的影響。

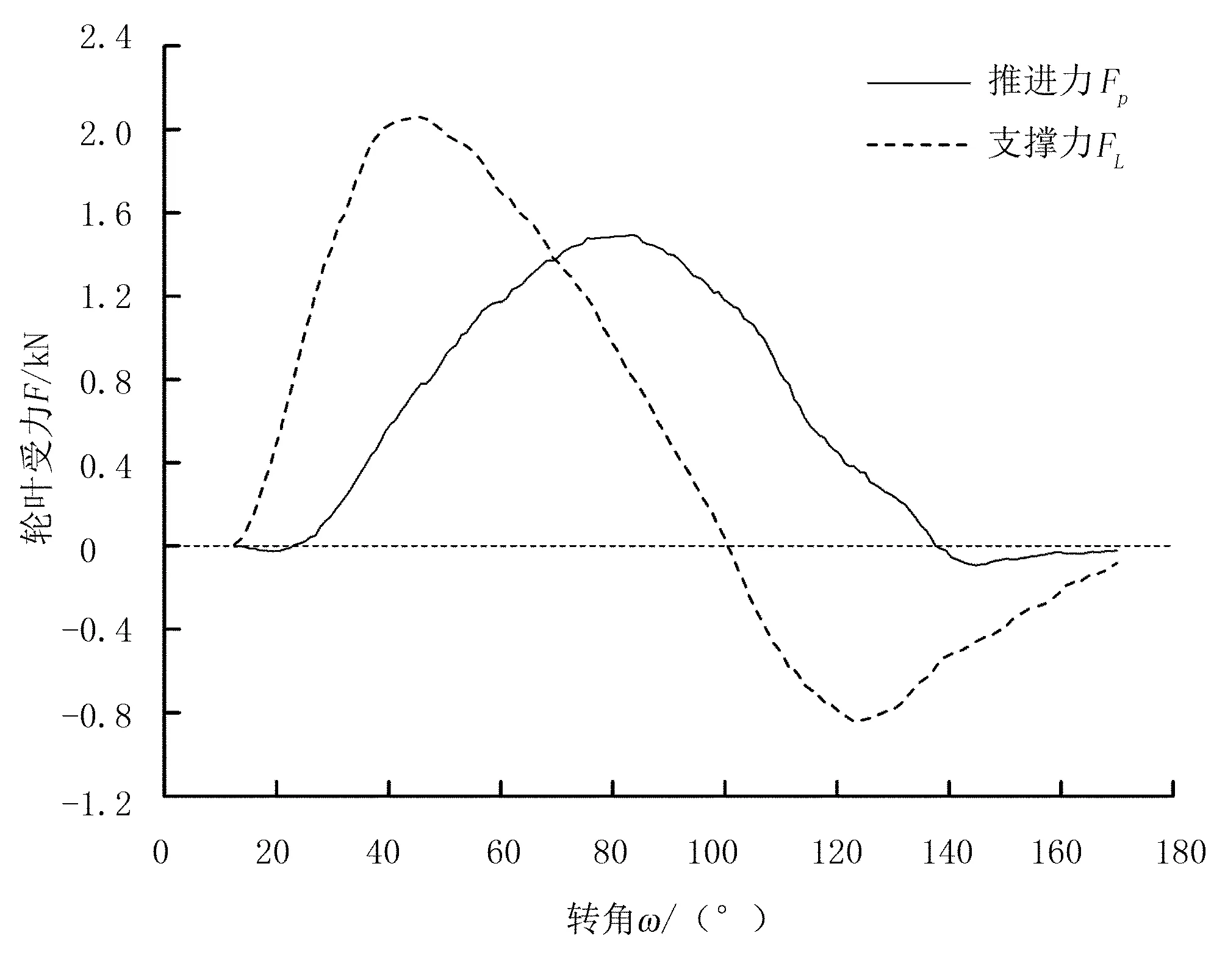
圖5 輪葉推進力Fp和支撐力FL變化曲線Fig.5 Pull force and lift force on the lug with turning angle

為衡量單輪葉驅動性能，在此分別對推進力做功WFp及驅動效率η參數進行定義：

1)推進力做功WFp。輪葉與土壤相互作用過程中，輪葉水平速度v恒定，推進力Fp為一個隨時間變化的量，推進力做功WFp可以反應推進力Fp的平均大小，因而WFp相比Fp的最大值，能更好地反應輪葉驅動效果，其公式為

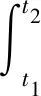
(2)

其中，t1為輪葉開始進入土壤的時間；t2為輪葉脫離土壤的時間。

2)驅動效率η。驅動效率η是表征單輪葉驅動性能的重要參數，公式為

(3)

其中，W總為t1～t2時間段內系統消耗的總功，可以從仿真結果中直接提取。

2.1 驅動面傾角

驅動面傾角α會對土壤推進力Fp及支撐力FL產生較大的影響，在此首先對驅動效率和推進力做功WFp隨驅動面傾角α改變的變化規律進行研究，結果如圖6所示。由圖6中可以看出：隨著α的增加，η及WFp均呈現先增大后減小的趨勢，且在α=4°時，η和WFp達到最大值，分別為40.56%和116.73J。這是因為在一定范圍內減小驅動面傾角α可使輪葉在入土階段所受的土壤支撐力Fp減小，從而減小輪葉滾動阻力；但α過小會使得輪葉在出土過程中所受土壤的滾動阻力增大，因此輪葉驅動面傾角α最優值為4°。

圖6 驅動效率及推進力做功隨驅動面傾角變化曲線Fig.6 Driving efficiency and work of pull force with different driving-surface angles

2.2 軸向角度

軸向角度θ是輪葉與輪轂軸線的夾角，在輪葉寬度B一定的情況下，θ的改變會影響輪葉軸向相對寬度B′，從而對Fp及FL產生影響。其中，驅動效率η和推進力做功WFp隨軸向角度θ改變的變化規律如圖7所示。從圖7中可以看出：隨著θ的增加，WFp先緩慢減小，當θ>25°附近開始迅速減小，這是因為B′總是隨著θ的增加而減小。從而Fp與FL隨之減小，進而WFp也隨之減小；η則是先緩慢增加而后迅速減小，并在θ=25°時達到峰值，此時η=41.66%，故輪葉軸向角度θ=25°時單輪葉驅動性能最好。

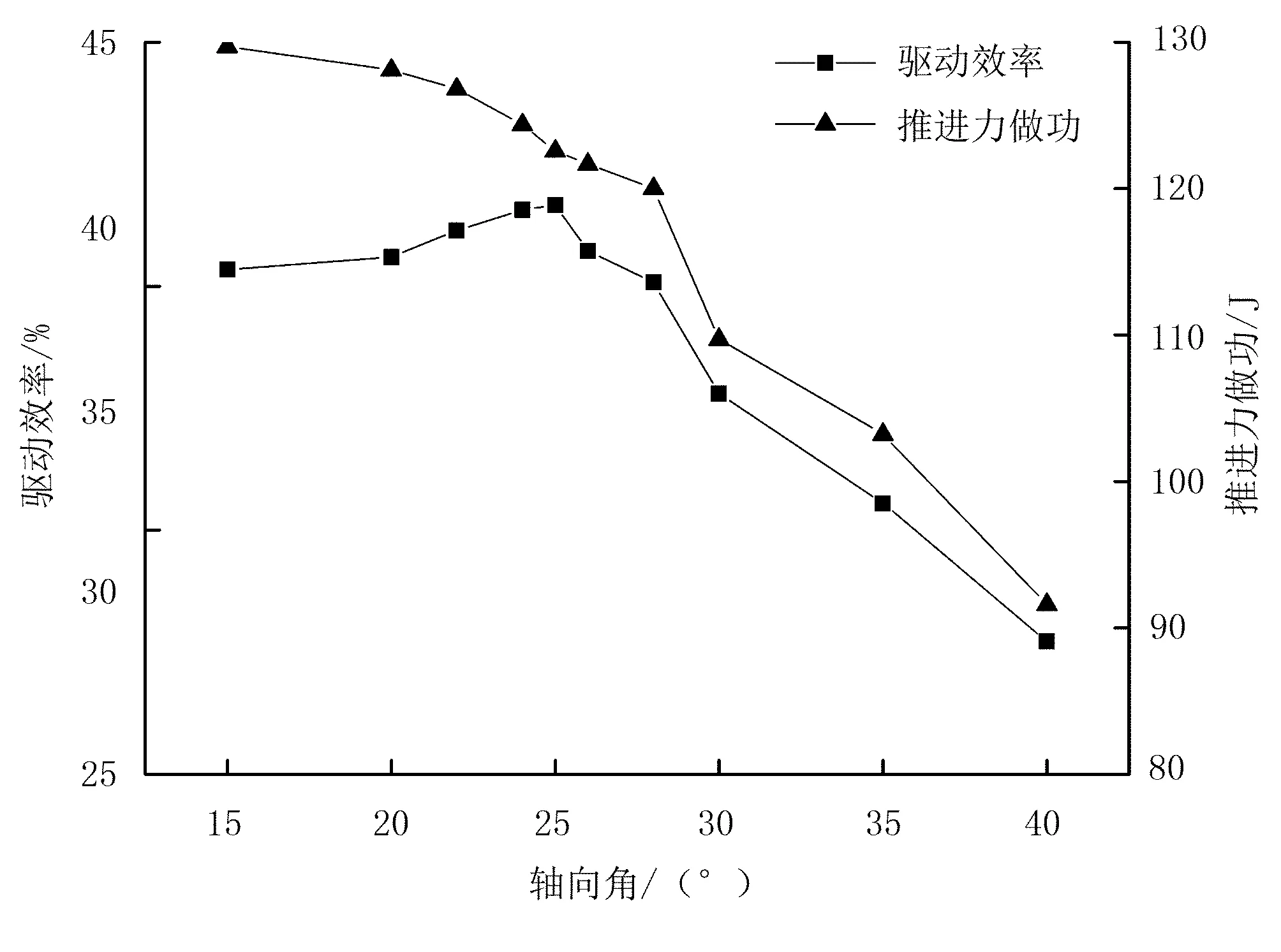
圖7 驅動效率及推進力做功隨軸向角變化曲線Fig.7 Driving efficiency and work of pull force with different axial angles

2.3 輪葉厚度

理論分析可知：輪葉厚度b值過大會使輪葉運動過程中輪葉厚度在水平方向的推土作用明顯，從而使推進力合力變小，降低驅動效率。圖8是不同輪葉厚度b下的推進力做功WFp及輪葉驅動效率η變化曲線。從圖8中可以看出：隨著b的增加WFp先緩慢增加，并在b=6mm時達到最大值為116.79J，而后隨著b的繼續增加WFp先緩慢后迅速減小；η在b=6mm處取得最大值，此時η=41.93%，且隨著b的繼續增加，η同樣先緩慢后迅速減小，故優化后的輪葉厚度b=6mm。

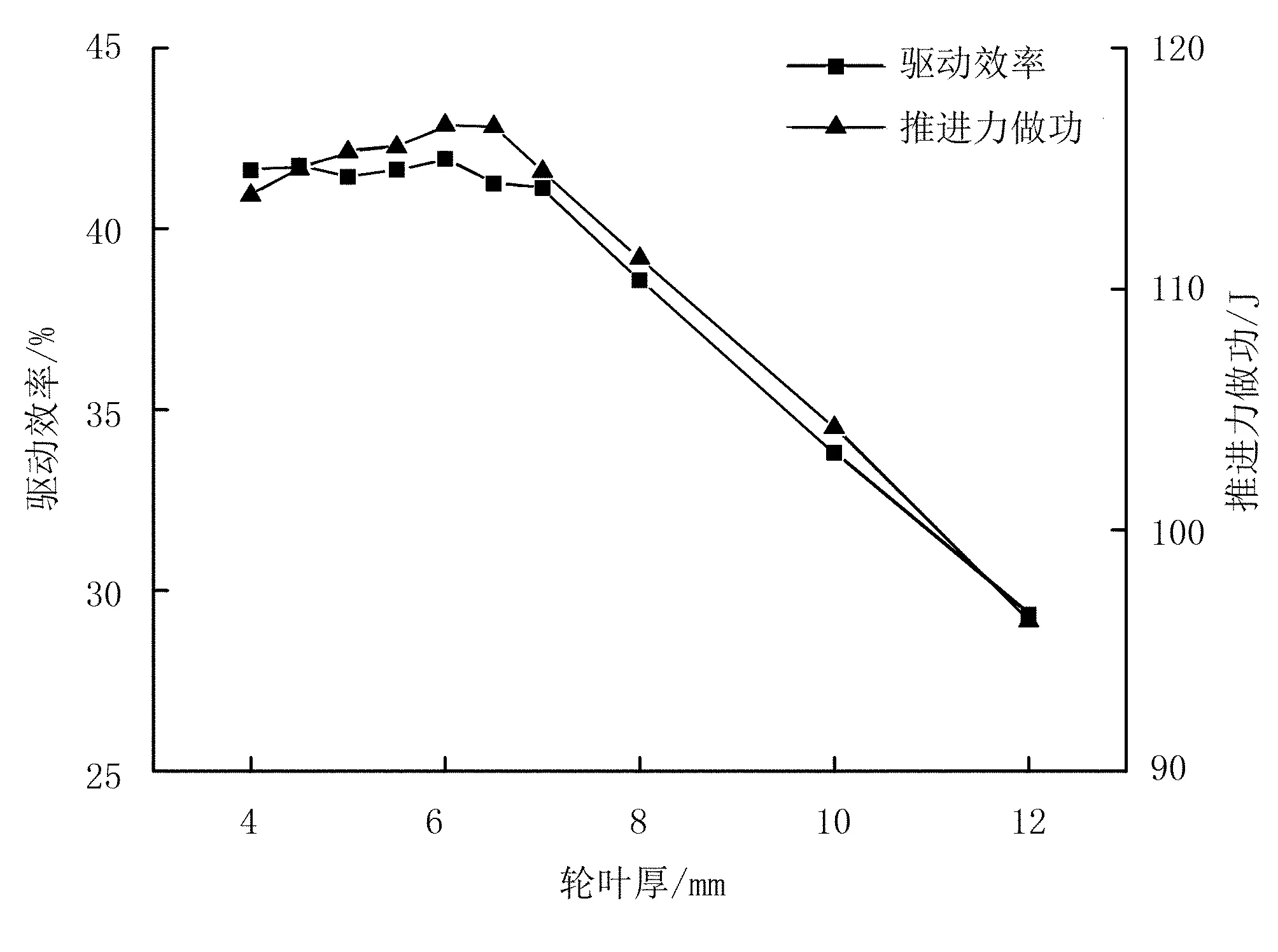
圖8 驅動效率及推進力做功隨輪刺寬變化曲線Fig.8 Driving efficiency and work of pull force with different lug width

2.4 優化前后對比

原輪葉結構參數5°-30°-8mm(驅動面傾角-軸向角-輪刺寬)，優化后輪葉結構參數為4°-25°-6mm。表2是優化前后輪葉最大支撐力、最大推進力和驅動效率對比。優化后輪葉最大支撐力由優化前的2.09kN降低至2.01kN，降低3.83%；最大推進力由1.45kN提升至1.59kN，增加9.66%；推進力做功由111.27J提升至126.54J，提升了13.72%。驅動效率由38.58%提升至46.43%，提升20.35%，即優化后的輪葉在保證足夠大的推進力的前提下(推進力增加9.66%)，減小了支撐力，并提升了20.35%的驅動效率。

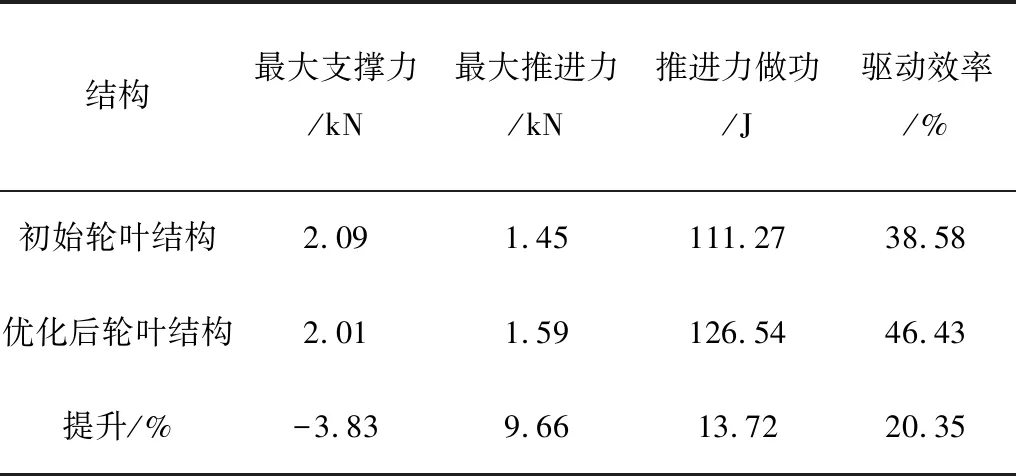
表2 單輪葉優化前后驅動性能對比Table 2 Comparison of the driving performance before and after optimization

3 結論

首先建立了輪葉-土壤動力學仿真模型，對滑轉率為25%工況下單輪葉驅動面傾角、軸向角度及輪葉厚度對驅動性能的影響進行了分析，在此基礎上對HH709S型船式拖拉機葉輪輪葉結構參數進行了優化，優化后的輪葉結構參數為4°-25°-6mm(驅動面傾角-軸向角-輪刺寬)。優化后最大支撐力減小3.83%，最大推進力提升9.66%，推進力做功提升13.72%，驅動效率提升20.35%。研究結果對船式拖拉機水田驅動葉輪結構的設計提供了指導，對提高船式拖拉機作業效率具有重要作用。