基于月值氣象數據和Penman-Monteith公式的流域蒸散發量計算

湯寅飛

（山西省水資源研究所，山西 太原 030024）

0 引言

蒸散發是水文循環中自降水到達地面后由液態或固態轉化為水汽返回大氣的階段，是水文循環中必不可少的組成部分[1]。由于水資源合理利用與管理定量化的迫切要求，蒸散發問題越來越受到人們的重視[2]。目前計算潛在蒸散發量的方法很多[3]，每種方法都有各自的優缺點和適用條件。聯合國糧農組織(FAO)推薦使用Penman-Monteith公式作為計算參考作物蒸散量的標準方法，這一方法以能量平衡和水汽擴散理論為基礎，具有較充分的理論依據和較高的計算精度，無需根據不同氣候條件進行參數校正，可直接應用[4]。以汾河流域為例，基于月值氣象數據和Penman-Monteith公式計算汾河流域蒸發量，并與Thornthwaite方法進行對比分析。

1 流域概況

汾河流域位于山西省中部和西南部，流域面積39471km2，是黃河第二大支流，流經山西6個地市，占山西省國土面積的25.3%，是山西省工業集中、農業發達的主要地區，占全省水資源利用總量的46.5%，見圖1。

因汾河流域比較大，不同位置的自然環境差別很大，在對汾河流域進行分析時，按其自然特征，習慣上分為上游（太原市蘭村水文站以上）、中游（蘭村至洪洞石灘水文站）、下游（石灘至入黃口）。

本文選取了汾河流域及周邊13個具有代表性的氣象站1960年1月至2015年12月共56年的月值氣象觀測資料，數據全部來自于中國氣象數據網。站點信息見表1。

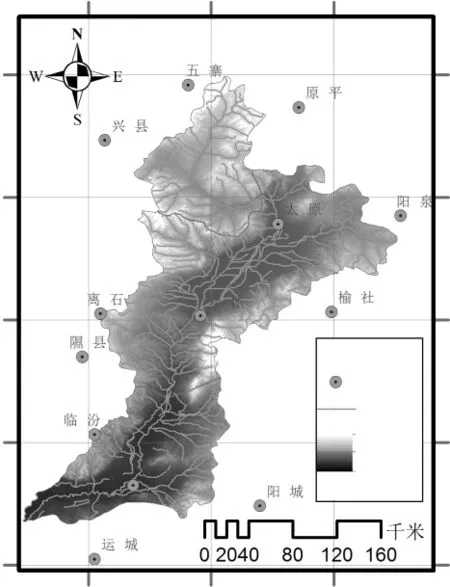
圖1 汾河流域水系圖

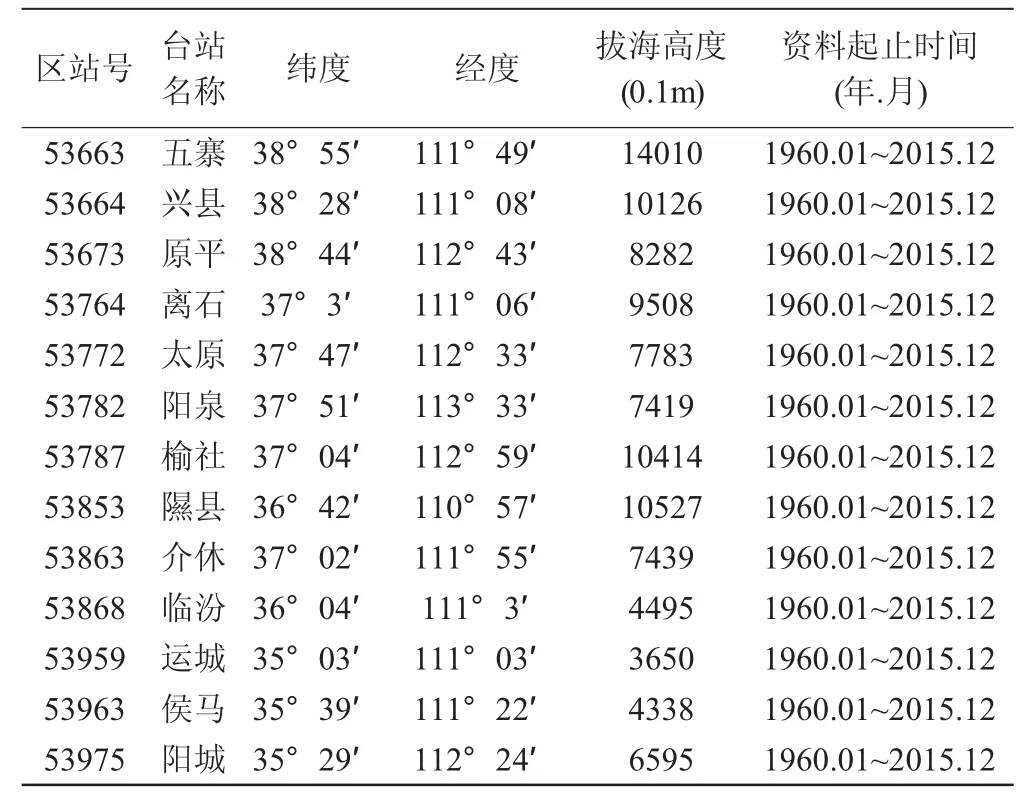
表1 氣象站臺表

2 計算方法

2.1 Penman-Monteith公式

標準化、統一化后的Penman-Monteith公式為：

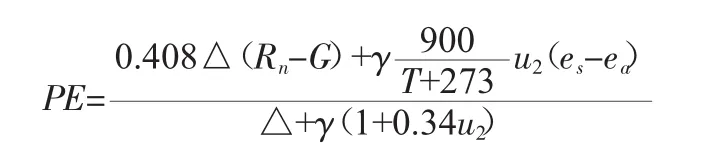
式中：PE 為可能蒸散量，mm·d-1；Rn為地表凈輻射，MJ·m-1·d-1；G 為土壤熱通量，MJ·m-2·d-1；T 為日平均氣溫，℃；u2為 2 m 高處風速，m/s；es為飽和水汽壓，kPa；ea為實際水汽壓，kPa；Δ 為飽和水汽壓曲線斜率，kPa·℃-1；γ 為干濕表常數，kPa·℃-1。

利用FAO Penman-Monteith公式計算參考作物蒸散量的資料時間步長范圍為小時、日或月，資料時間尺度的選取取決于計算的目的、計算需要的精度及可獲取的氣象資料的時間尺度[5]。由上述公式可知，Penman-Monteith公式的各項參數是以日值數據給出的，一般認為，用日值氣象數據計算蒸發量是最準確的。但是由于數據獲取途徑、計算目的與計算精度等原因，很多研究直接利用月值數據計算蒸發量[5～9]。利用月值數據按照Penman-Monteith公式計算蒸散發量時，不能直接把日值參數直接對應月值參數來計算，每個參數都需要重新進行換算。計算過程主要參考《氣象干旱等級》[10]，有兩點需要注意。

（1）相對于凈輻射Rn，土壤熱通量G是很小的量，用日值數據計算蒸散發量時，土壤熱通量通常忽略不計。但用月值數據計算時，此項不能忽略，計算公式為：

式中：G 為土壤熱通量，MJ·m-2·d-1；Tmonth,i為第 i月的平均氣溫，Tmonth,i-1為上月平均氣溫，℃。公式中的平均氣溫T取月值數據的平均氣溫，第一個月的土壤熱通量假設為0。

（2）中國氣象數據網提供了總輻射、凈輻射、散射輻射、直接輻射和反射輻射五種輻射數據，這些數據可直接計算地表凈輻射。但是由于輻射觀測站和氣象觀測站在數量上不匹配（氣象觀測站699個，輻射觀測站130個），觀測年限不統一，輻射資料在趨勢分析、持續性分析中很難與氣象數據結合。因此在應用Penman-Monteith公式計算蒸散發量時，一般用氣象數據間接計算出地表凈輻射，而不應用輻射數據。

用月值數據按照Penman-Monteith公式計算蒸發量時，需提供測站的海拔高度與緯度，提供平均最低氣溫、平均最高氣溫、氣溫、風速、平均相對濕度和日照時數6個月值要素。這6個要素是氣象站測量的常規要素，一般不會出現缺測的情況，可以滿足長時間序列蒸散發量的計算。

2.2 Thornthwaite公式

Thornthwaite方法是《氣象干旱等級》是中提出的另一種蒸發計算方法，它以月平均氣溫為主要依據，并考慮緯度因子，是一經驗公式，計算方法簡單，適用性強。計算公式為：

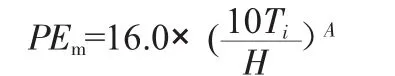
式中：PEm為可能蒸散量，mm/月；Ti為月平均氣溫，℃；H為年熱量指數；A為常數。

3 計算結果及分析

3.1 Penman-Monteith公式計算結果及分析

汾河流域蒸發蒸發計算結果及年際變化見表2、圖2。

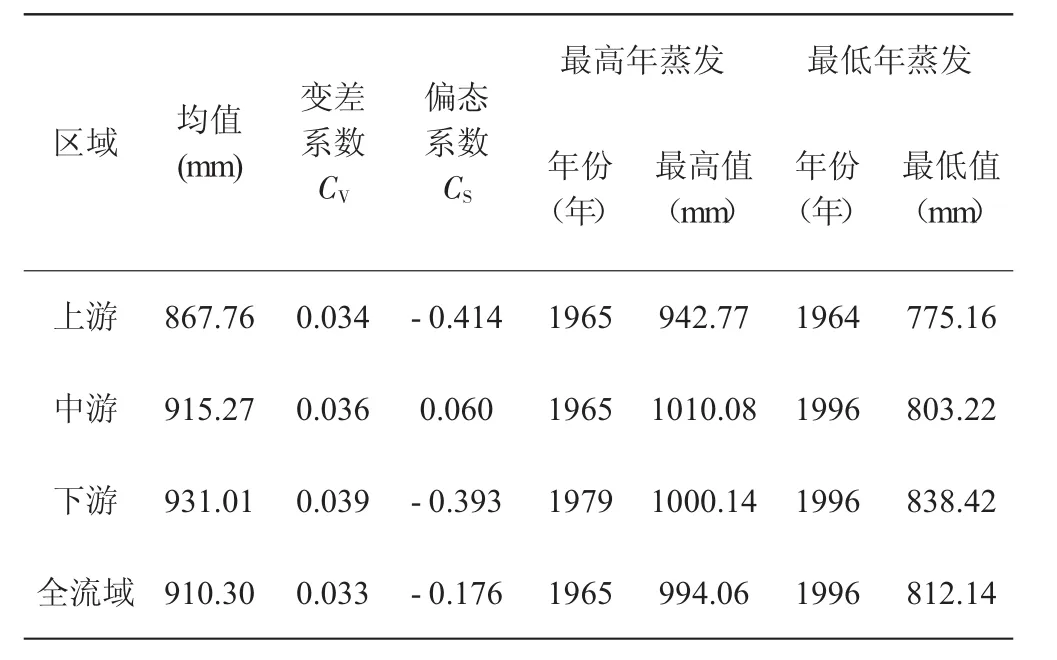
表2 汾河流域蒸發計算結果表

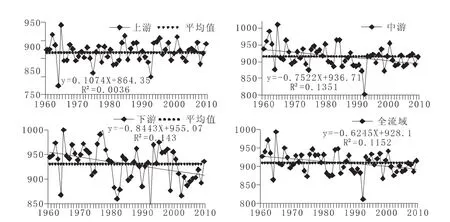
圖2 汾河流域蒸發年際變化圖

由表2、圖2可知，汾河流域蒸發量由上游至下游逐漸增加，全流域年均蒸發量為910.3 mm；變差系數、偏態系數差別不大，流域最高年蒸發量為994.06 mm，最低年蒸發量為812 mm；流域上游年蒸發量呈總體上升趨勢，趨勢不明顯；中游、下游和全流域蒸發量呈下降趨勢，下降趨勢明顯。

3.2 與Thornthwaite公式計算結果對比分析

汾河流域用Thornthwaite公式計算蒸發蒸發的結果及年際變化見表3、圖3。

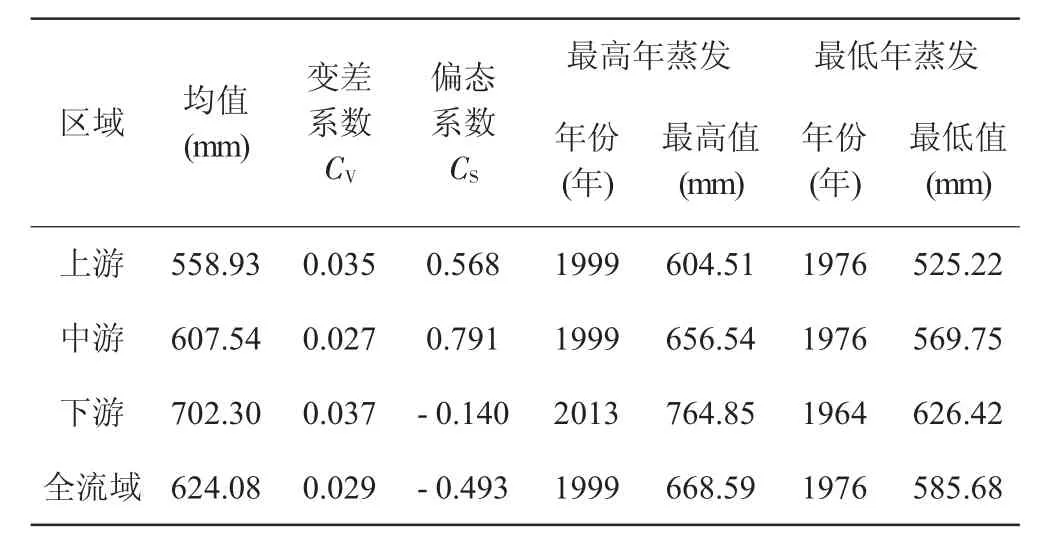
表3 汾河流域蒸發計算結果表（Thornthwaite方法）

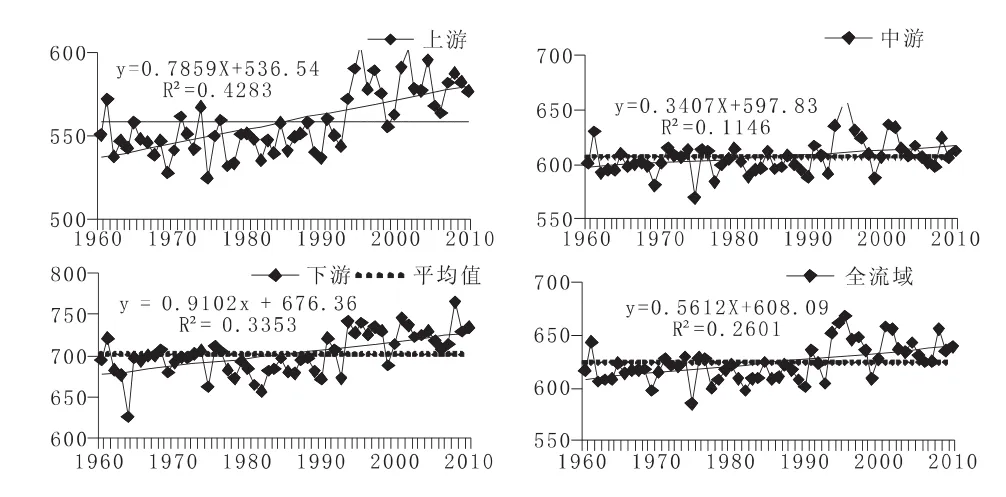
圖3 汾河流域蒸發年際變化圖（Thornthwaite方法）

由計算結果可知，用Thornthwaite方法計算汾河流域蒸發量與Penman-Monteith公式有很大不同。蒸發量由上游至下游逐漸增加，全流域年均蒸發量為627.08 mm；變差系數差別不大，上游、中游的偏態系數超過0.5，全流域接近0.5；流域最高年蒸發量為668.59 mm，最低年蒸發量為585.68 mm，最值發生年份與Penman-Monteith公式計算結果不匹配；上游、中游、下游和全流域的蒸發趨勢均為明顯上升趨勢。

由于Thornthwaite方法是基于美國中東部地區的試驗數據提出的，對溫暖濕潤地區更加適用，溫度較低時計算結果偏小[11]。尤其是低于0℃時認為蒸發量為零，不符合實際。因為汾河流域冬季月平均氣溫大多低于0℃。在華北地區，Thornthwaite方法計算蒸發量誤差為30%左右[12]。汾河流域蒸發量計算Thornthwaite方法較Penman-Monteith公式偏小31.4%，可認為基于Penman-Monteith公式的計算結果是比較準確的。

4 結論

（1）蒸發是許多自然科學研究中重要的組成部分。Penman-Monteith公式以能量平衡和水汽擴散理論為基礎，既考慮了作物的生理特征，又考慮了空氣動力學參數，計算精度高，適應性強，應用廣泛。

（2）Penman-Monteith公式大多數基于日值氣象數據進行計算，但由于計算精度、研究范圍和計算目的的不同，通常用月值氣象數據計算蒸發量。該方法需要測站的海拔高度與緯度以及平均最低氣溫、平均最高氣溫、氣溫、風速、平均相對濕度和日照時數6個月值要素。

（3）選取汾河流域及周邊13個具有代表性的氣象站，應用56年的月值氣象要素對汾河流域的蒸發量進行計算。計算結果表明：汾河流域年平均蒸發量為910.30 mm，最大蒸發量為994.06 mm，最低蒸發量為812.14 mm，變差系數為0.033，偏態系數為-0.176，總體趨勢為逐年遞減。

（4）應用Thornthwaite方法對汾河流域蒸發量進行計算，汾河流域年均蒸發量為624.08 mm，較Penman-Monteith公式偏小31.4%。對比其他研究成果，可認為兩種方法計算結果均是合理的。但是蒸發趨勢、最值發生年份有很大不同，需進一步研究分析。