基于半圖解法的MATLAB程序和Excel在水庫調洪演算中的聯合運用

安航永，趙文龍，張雅萍

（1.廣州禺山水務勘測設計股份有限公司，廣東 廣州 511400；2.黃河水利水電開發總公司，河南 鄭州 450000；3.黃河建工集團有限公司，河南 鄭州 450000）

調洪演算是水庫規劃設計中的重要內容之一，其目的是根據已知的水位～庫容關系、洪水過程、調洪調度方案和起調水位，演算并輸出各計算時段末的庫水位、泄流量和庫容變化量等[1]。調洪演算計算方法主要有試算法、半圖解法、數值解法等，其中半圖解法是最為簡單、有效的演算方法[2]。但是，隨著計算機的普及，適合編程的數值解法得到快速發展，半圖解法逐漸在實用中淡出[3]。筆者借助MATLAB強大的數據處理和數據插值能力以及Excel友好的人機交互能力，程序化半圖解法，使其能夠更加高效、便捷的解決調洪演算問題。

1 MATLAB在數據插值方面的應用

MATLAB內置多種數據插值函數，可以進行一維數據插值（interp1）、二維數據插值（interp2）和三維數據插值（interp3）等。在工程計算中，較常用的插值函數為interp1，其運用的一般格式為：y=interp1（X，Y，x，method），其中 method 為插值方法[4]。常用的插值方法有：nearest（最近鄰點插值）、linear（線性插值）、spline（三次樣條函數插值）、pchip（分段三次Hermite插值）等，函數默認插值方法為linear。

2 半圖解法基本原理

水庫調洪演算的基本原理是求解水庫的水量平衡方程[5]：

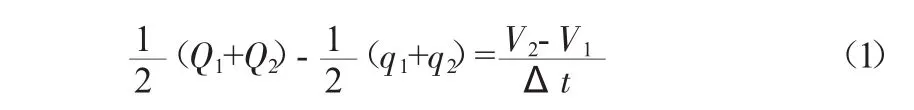
半圖解法在求解過程中將水量平衡方程改寫為[6]：

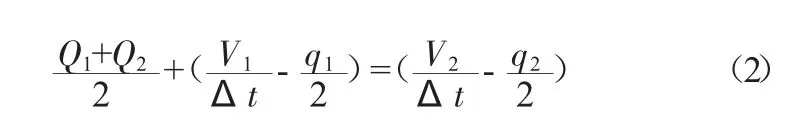
式中：Q1、Q2分別為計算時段初、末的入庫流量，m3/s；q1、q2分別為計算時段初、末的下泄流量，m3/s；V1、V2分別為計算時段初、末水庫的蓄水量，m3；Δt計算時段，s。

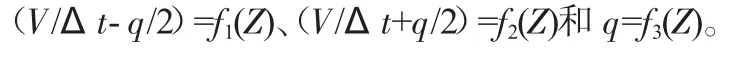
半圖解法計算步驟如下：

（1）根據水位～庫容關系、水位～泄流關系以及計算時段等繪制輔助曲線，見圖1。

（2）確定起調水位 Z1，及相應的q1、V1，計算各時段平均入庫流量Qp。

（3）在圖1水位坐標軸上確定Z1位置，記為a點。作水平線ac交 A線于b點，使 bc=Qp。因A 線為（V/Δt-q/2）=f1(Z)，則 ab 等 于 （V1/Δt-q1/2），ac 等 于 Qp+（V1/Δt-q1/2）=（V1/Δt+q1/2）。

（4）在c點做垂線交B線于d點，由d點作水平線de交Z坐標軸于 e點，可見 de=ac=（V2/Δt+q2/2）。因 B線為（V/Δt+q/2）=f2(Z)，d 點位于 B 線上，則 e點為 Z2值。

（5）過de與C線交點f作垂線交q坐標軸于g點，則g點為q2值。

（6）根據Z2值，查水位～庫容曲線可得V2。

（7）將 e點的 Z2值作為第二時段的 Z1，重復（2）～（6）即可得下一時段的特征值。由此逐時段進行計算，即可完成全部計算。

圖1 半圖解法輔助曲線

3 計算程序及使用方法

本方法由Excel完成基礎數據的錄入工作，然后通過MATLAB程序調用基礎數據并完成調洪演算。

（1）數據錄入

首先，根據程序要求創建名稱為data的Excel文件。在data.xls內建立5個工作表，分別用來存儲洪水過程（RuLiu）、水位 ～ 庫容關系（KuRong）、水位 ～ 泄流關系（XieLiu）、起算條件（Set）以及演算結果（OutPut）。各工作表數據錄入格式見圖2～圖5。

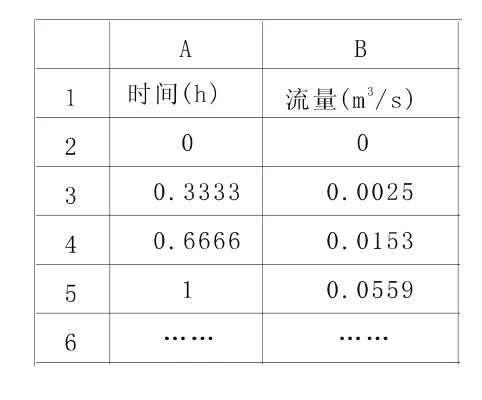
圖2 洪水過程錄入格式

圖3 水位～庫容關系錄入格式

圖4 水位～泄流關系錄入格式

該程序通過MATLAB中xlsread函數自動調用data.xls中基礎數據，采用interp1完成半圖解法中的插值運算，然后通過xlswrite函數將演算結果輸出至“OutPut”工作表，整個計算過程均由計算機完成，即提高了演算速度又避免了人工繪圖和讀數的誤差。

4 應用實例

以官涌水庫調洪演算為例，驗證該方法的方便適用性。官涌水庫位于廣州市番禺區，為小（2）型水庫，水庫大壩為均質土壩，壩高9.53 m，壩頂高程19.97 m，設計洪峰流量為2.93 m3/s，校核洪峰流量為4.39 m3/s。官涌水庫泄流建筑物為一座1.5 m×1.55 m（寬×高）開敞式溢洪道，溢洪道底高程16.82 m。

官涌水庫設計洪水過程、水位～庫容關系、水位～泄流關系見圖6～圖8，水庫調度原則為敞泄，即起調水位為16.82 m。

圖6 設計洪水過程線

圖7 水位～庫容關系曲線

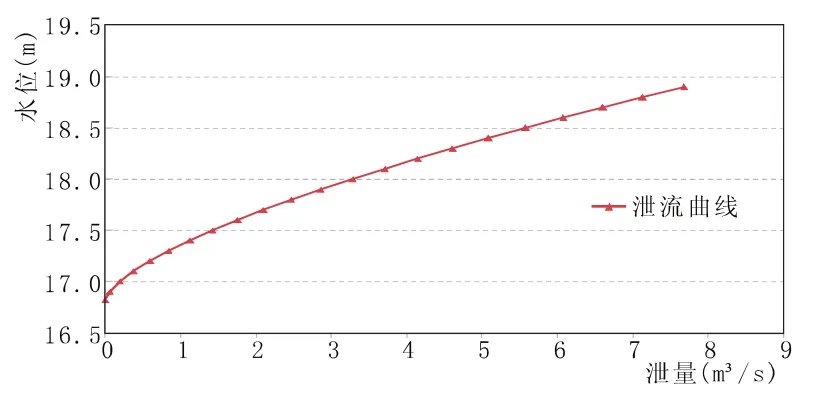
圖8 水位～泄流關系曲線

根據官涌水庫設計洪水過程、水位～庫容關系、水位～泄流關系及水庫調度原則，在錄入基礎數據后運行MATLAB程序完成計算。程序輸出結果包括入庫流量（m3/s）、出庫流量（m3/s）、時段蓄量（萬 m3）、庫容（萬 m3）和水位（m），演算結果見圖9～圖10，結果輸出格式如表1。

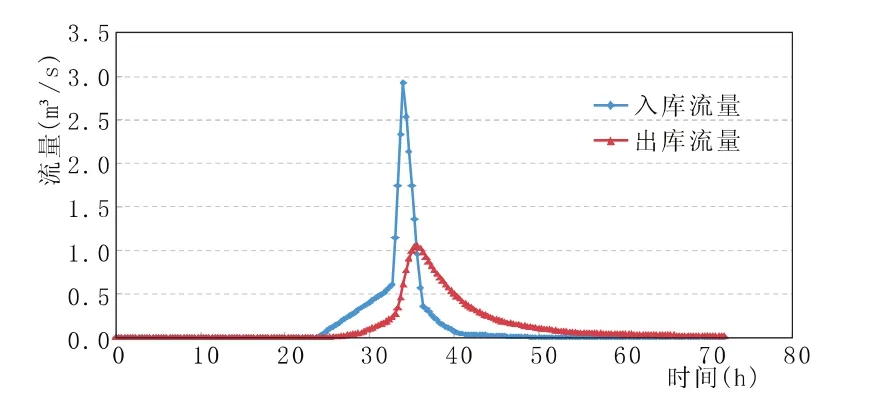
圖9 調洪演算結果（出/入庫流量）

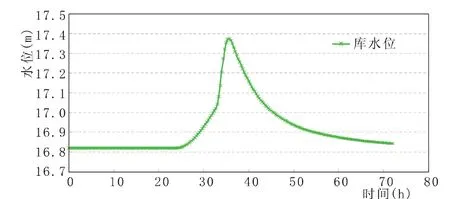
圖10 調洪演算結果（庫水位）

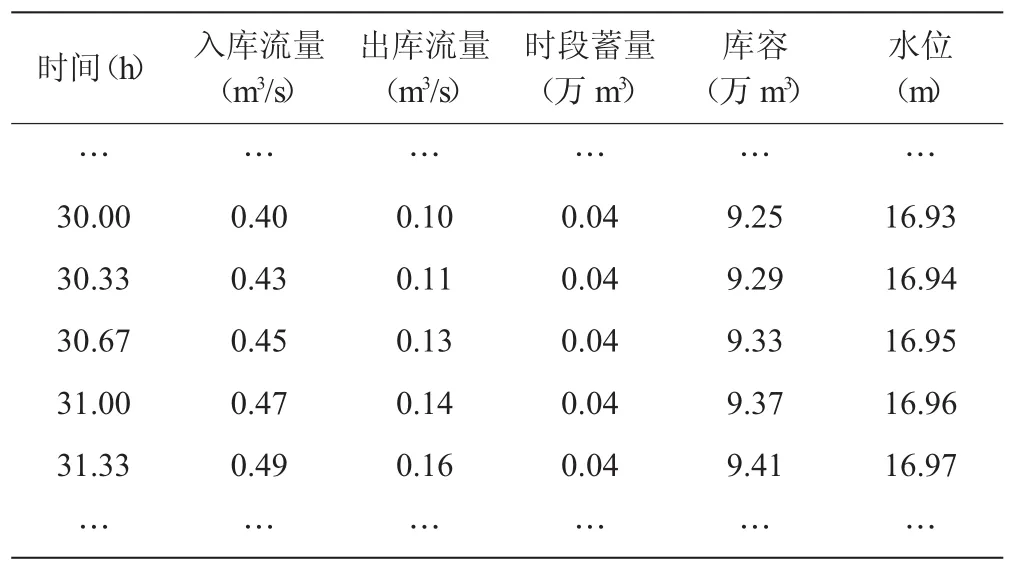
表1 演算結果輸出格式

5 結語

本文以官涌水庫調洪演算為例，聯合運用MATLAB程序和Excel，方便、快速的完成了官涌水庫調洪演算工作。該方法不僅操作方便、計算迅速，而且避免了人工繪圖和讀數的誤差，計算精度也得以提高。可見，以半圖解法為理論基礎，聯合運用MATLAB程序和Excel解決水庫調洪演算問題是一次成功的嘗試，不僅解決了半圖解法的程序化問題，而且為廣大水利工程技術人員提供了一個解決水庫調洪演算工作的方便、快捷的方法。