注重幾何直觀，著眼能力提升
——中考“旋轉伴隨相似模型”專題復習例談

☉浙江省衢州市衢江區廿里鎮初級中學 徐建兵

中考復習課教學是學生核心素養和能力提升的過程，《義務教育數學課程標準（2011年版）》（以下簡稱《標準》）指出：幾何直觀主要是指利用圖形描述和分析問題，可以把復雜的問題變得簡明、形象，有助于探索解決問題的思路，預測結果.旋轉是一種基本的圖形變換，若將三角形繞著一個頂點旋轉，再放大（或縮小）得到新的三角形，連接對應點后會伴隨第二次相似的出現，這兩個相似以過旋轉中心點的四條線段成比例為紐帶，這一伴隨關系，在很多時候能使復雜問題簡明化.筆者就針對此類基于旋轉的三角形相似模型進行教學實踐，讓學生在感知、應用和構造“旋轉伴隨相似模型”中培養幾何直觀素養,提升解題能力．

一、呈現模型，知其性明其理

例1如圖1，在△ABD與△CBE中，已知∠ABD=∠CBE，要使△ABD與△CBE相似，還需要添加什么條件？當△ABD △CBE時，連接對應點AC和DE，還有沒有其他三角形相似呢？若有，請寫出對應邊的比例式.

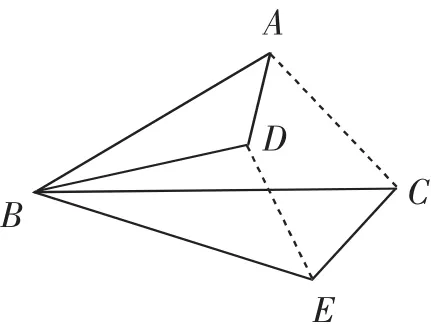
圖1

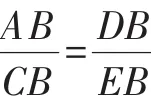
二、應用模型，曉其法通其性

例2 如圖2，△ABC與△EDC均為正三角形，B、A、D三點在一直線上，連接AE，可得到AE//BC的結論.如圖3，在△ABC與△EDC中，AB=AC，DE=CE，∠B=∠ECD，上面的結論是否還成立？若成立，請說明理由.

圖2

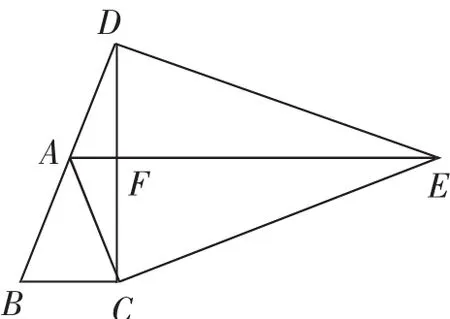
圖3

解析:如圖3,通過觀察發現，△EDC可由△ABC繞點C旋轉后放大得到，因此伴隨著會出現△DBC△EAC，所以∠B=∠EAC.因為∠B=∠ACB，所以∠EAC=∠ACB，所以AE//BC.

點評:在復雜的圖形中發現基本模型需要學生具有一定的幾何直觀素養,需要有敏銳的觀察能力.如圖2,△ACB和△EDC中,具有AC=BC,DC=EC的特殊性，因此伴生出△DBC和△EAC既相似又全等.這與八年級全等章節中出現的“手拉手的全等模型”相一致，體現全等是相似的特殊形式，這樣有利于形成知識之間的相互聯系,使知識更加系統化.此外，本題的教學設計中，筆者還把另一個重點放在學生如何尋找二次相似的方法指導上，第一步找顯性的三角形相似，第二步找出第一次相似的對應點，第三步連接對應點構成新的一對相似三角形，通過方法指導讓學生知曉它的用法，精通它的性質，提升學生的幾何直觀素養.

三、構造模型，培養創造性思維

例3如圖4，正△ABC與正△DEF的邊AB、DE的中點重合于點O，△DEF繞點O旋轉一定角度，連接AD、CF，當AD=1時，求CF的長度.

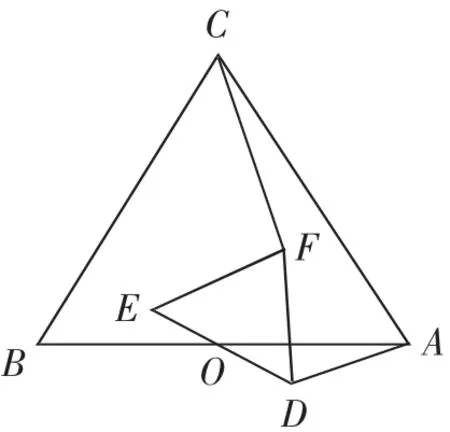
圖4

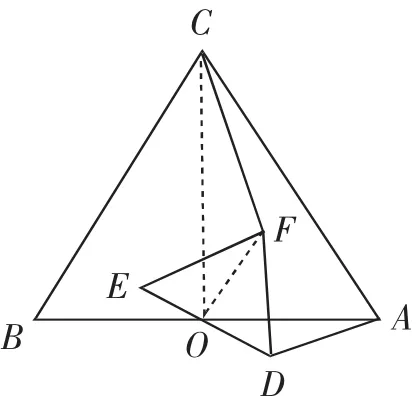
圖5

解析：如圖5，連接OC、OF.Rt△AOC可由Rt△DOF繞點O旋轉后放大得到，因此伴隨著會出現△AOD和△COF，

例4如圖6，正方形AEFG是正方形ABCD繞其頂點A旋轉一定角度縮小后的圖形，連接DG和CF，求線段DG與CF的比值.

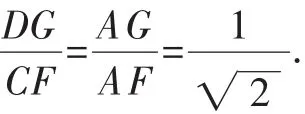
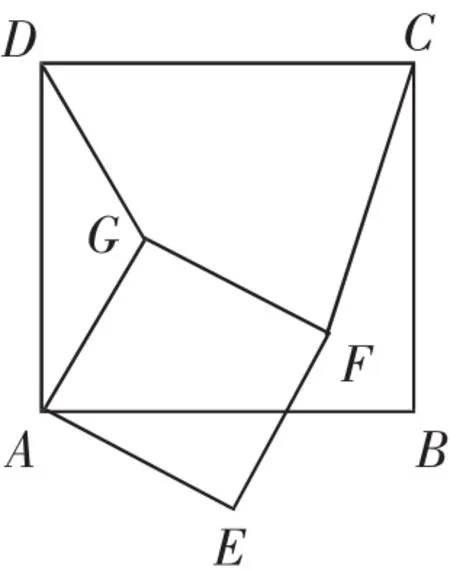
圖6

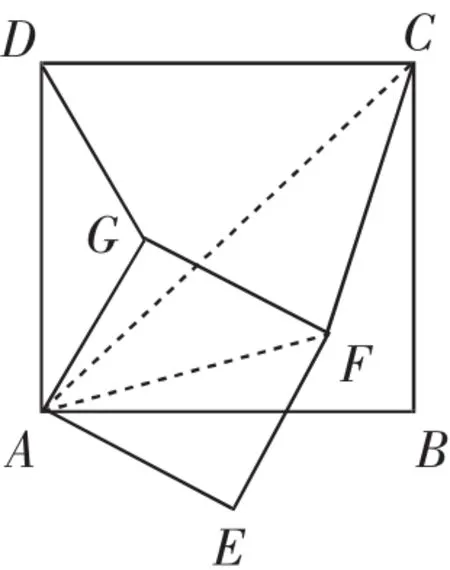
圖7

點評：《標準》指出：數學教育既要使學生掌握現代生活和學習中所需要的數學知識與技能，更要發揮數學在培養人的理性思維和創新能力方面不可替代的作用.從例3的圖形中看不出“旋轉伴隨相似”的模型，它是由兩個正三角形繞著一條邊的中點旋轉，這就需要學生有創造性的思維，通過添加輔助線，構造出“旋轉伴隨相似模型”，當連接OC、OF時，會出現Rt△AOC由Rt△DOF繞點O旋轉后放大得到，因此伴隨著會出現△AOD △COF.把毫無關聯的線段AD、CF聯系在相似三角形的對應邊上.例4是正方形旋轉.當對應點連接時會出現△ADG △ACF.DG和CF并不在需要的相似三角形中，這就需要連接對角線AC和AF，構造出Rt△ACD由Rt△AFG繞點O旋轉后放大得到，伴隨著會出現△AGD △AFC，從而解決問題.在我們的教材中，很多四邊形相關內容都是利用三角形知識來解決，體現了數學中的化歸思想，這種數學思想的滲透有利于學生形成自主學習的能力.課堂中通過體會如何構造模型培養學生的幾何直觀與創造性思維.

四、拓展模型，經驗積累中提升素養

例5如圖8，已知A是第一象限內橫坐標為2的一個定點，AC⊥x軸于點M，交直線y=-x于點N，若P是線段ON上的一個動點，∠APB=30°，BA⊥PA，點P在線段ON上運動時，點A不變，點B隨之運動，則點P從點O運動到點N時，求B點運動的路徑長.

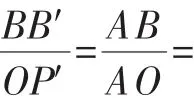
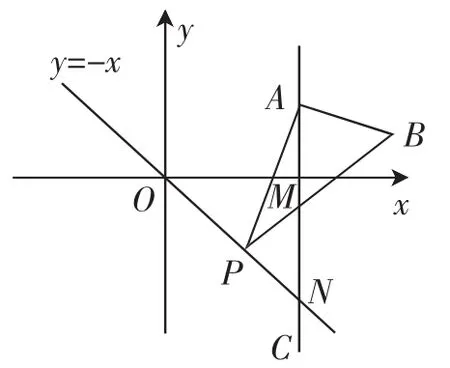
圖8

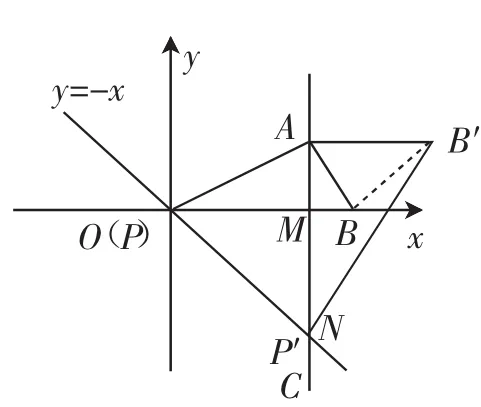
圖9

點評：本題源于2013年浙江省湖州市初中畢業學業考試填空題的壓軸題第16題，本題考查坐標平面內由相似關系確定的點的運動軌跡，難度很大，需要學生具有較好的幾何直觀素養，能從問題中找到“旋轉伴隨相似模型”的影子，利用相似關系求出點B運動路徑的長度，運用“旋轉伴隨相似模型”可以大幅簡化計算，避免陷入坐標關系復雜運算之中.類似的應用還出現在2017年浙江省衢州市初中畢業學業考試第24題的第（2）問中：“在直角坐標系中，過原點O及點A（8，0）、C（0，6）作矩形OABC.連接OB，點D為OB的中點.點E是線段AB上的動點，連接DE，作DF⊥DE，交OA于點F，連接EF.已知點E從A點出發，以每秒1個單位長度的速度在線段AB上移動，設移動時間為t秒.如圖10，當點E在線段AB上移動的過程中，∠DEF的大小是否發生變化？如果變化，請說明理由；如果不變，請求出tan∠DEF的值.”將△DEE′繞點D旋轉，再擴大（或縮小）得△DFF′，在這個變化過程中，伴隨著第二次相似，即當E在AB邊上運動時，都有△DEF △DE′F′，得到∠DE′F′=∠DEF是個定值，所以tan∠DE′F′=?.因此學生對這種模型的經驗積累，有利于提升學生的幾何直觀素養和解題能力.

圖10

學習需要天分，學習也需要積累，“旋轉伴隨相似模型”是一種圖形特性的經驗積累.《標準》指出，數學活動經驗的積累是提高學生數學素養的重要標志.幫助學生積累數學活動經驗是數學教學的重要目標.數學活動經驗需要學生在不斷經歷、體驗各種數學活動中，在“做”與“思”的過程中進行積淀，因此學習除了善學善思，還應做到善于總結經驗.