關于提高初中數學核心素養的有效措施探究
福建省石獅市石光中學 蔡雙玉
什么是數學學科的核心素養?這個問題至今為止在學術界沒有一個標準統一的答案。簡要來說,數學核心素養建立在學生對數學知識熟練掌握的基礎之上,是學生對數學知識進行更高層次的綜合運用的能力,其中也包括學生的邏輯思維能力、思考方式等多個方面,由這些要素有機組合便構成了學生的數學核心素養。因而,數學核心素養的培養提高絕不能僅僅針對熟練掌握教材知識這一個方面,而是應該全方位、多角度、多方面地進行綜合提高,從而達到這一目標。那么,教師究竟應該采取什么有效措施,才能達到提高初中學生數學核心素養的目的呢?下面將從三個方面展開敘述。
一、培養學生的質疑能力
在初中教學階段,學生的思維大多數仍舊停留在小學階段,對于教師所講授的知識來者不拒,全盤吸收,而不加以甄別鑒定,對于教師部分與自己所學有所出入的話,也會下意識地認為是自己想錯了,必須跟著老師的思路走,與老師思維進行同化,這樣才能取得好成績。然而,越來越多的實踐證明,這樣的學習方式是完全錯誤的,尤其是在數學學科中,教師必須注重培養學生的質疑能力,使學生敢于質疑老師、質疑書本的權威性,在質疑的過程中漸漸培養自己解決數學問題的思維方式,從而使學生的數學核心素養得以提高。
例如,在教師教授“相反數”這一課時,會引入“負數”的概念,這與學生在小學階段所學的“數字都是大于等于0 的”相違背,如果學生對此不能勇敢地向老師提出疑問,即使在教師講過該知識點之后,也會在心里埋下疑惑的種子,在實際解題過程中有所混淆。因而,學生必須敢于質疑,再由教師做出解答:“實際生活中,我們說的‘數字’大多都是指數量,因而必須大于等于0,但是我們這里所講的‘負數’是在數學研究中引入的新概念,是為了方便大家進行更深層次的研究。”由此,學生的疑惑得到解答,對“負數”的概念也會更加明晰。
二、開發學生的思考方式
數學題是靈活多變的,尤其是在初中階段,與以往小學直接代入公式的簡單題型不同,數學問題更需要學生去思考著解決。因而,教師必須注重開發學生的思考方式,引導學生從多個角度、多個方面來進行解題,在這一過程中,學生從書本上學習到的基礎理論知識得到運用,在復雜多變的題型中,學生的思維方式也得以提升,從而增強了學生的邏輯思維能力,進而提高了學生的數學核心素養。
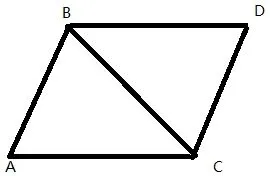
例如,在講授“全等三角形”這一課時,證明三角形全等共有五種方式。已知△ABC 和△BCD 的位置關系如圖,BC 為公共邊,AC ∥BD,且AC 與BD 相等,試證明兩個三角形全等。對于這樣一道證明題,有多種解法,學生可以結合這節課程內容所學,運用SAS 定理得出求證結果,但也可以利用之前平面圖形章節所學內容,利用兩邊平行且相等,得出四邊形ABDC 是一個平行四邊形,再根據平行四邊形的性質定理,運用SSS定理或AAS 定理得出結果。一道簡單的數學問題有多種不同的解法,因而教師應該注重開發學生的思考方式,培養學生從多角度解決數學問題的思路,而不應僅僅引導學生將目光簡單地停留在“答案正確即可”上面,當學生遇到更為復雜的問題時,也能夠恰當運用多種思路來解決數學問題,從而培養提高學生的數學學科核心素養。
三、提高學生的自主學習能力
數學學習是一個主動學習的過程,然而在初中數學課堂上,由于各種各樣的原因,或是出于羞怯,或是出于害怕,學生往往羞于表達自己的思考與想法,數學課堂的學習氛圍往往是沉悶而寂靜的,教師成為課堂教學過程中信息的全部發出者,而學生被動接受吸收這些信息,數學課堂完全淪為教師的“一言堂”。因而,教師必須加強引導,提高學生的自主學習能力,須知只有學生自己才能成為推動自身發展的核心動力,其余的外部因素諸如教學環境、課堂氛圍等不過是錦上添花而已。而自主學習能力不僅僅指學生在課堂上主動汲取吸收教師所講授的知識點的能力,還包括學生自身的自主探究能力,在學生的自主探究過程中,由于大量思考,學生不僅能夠將以往所學加以綜合運用,還能夠根據思考的想法得出新的學習體會,可謂一舉兩得。因而,教師注重提高學生的自主學習能力是十分必要且重要的。
例如,在教師教授“三角函數”這一知識點時,由于教師已經講解過正弦與余弦函數的相關基礎知識,根據正切函數的定義,在直角三角形中,正切函數是角的對邊與鄰邊的比值,那么能不能通過自主探究,得出幾個特殊的正切函數值呢?通過對比,能不能得出這些三角函數的值與其對應角的度數有什么關聯呢?當教師根據學生的知識掌握水平布置這樣一個自主探究任務時,學生就能夠通過課后大量思考與練習得出最終結論,在銳角范圍內,角的度數越大,正弦值與正切值越大,余弦值越小。
數學學科本身并不是學生通往大學路上的一塊“敲門磚”,而是學生應該貫穿學習與生活始終的一門工具類學科,不僅能夠解決實際生活中蘊藏的數學問題,也能在學習數學的過程中增強學生自身的邏輯思維能力,提高學生的數學學科核心素養,從而促進學生自身綜合全面發展。

