租船問題研究
廣東省廣州市天府路小學 陳欣言
在義務教育教科書數學四年級下冊第一單元《四則運算》的例5(課本第10 頁),主題是租船問題:游客有32 人,大船30 元每艘,可載6 人,小船24 元每艘,可載4 人,問怎么租船租金最少?課本上的策略是通過計算和比較得出結論:先盡量租人均價格便宜的船,再考慮不留空位,就會最省錢,這樣得到的方案是大船4 艘,小船2 艘。
經過思考,我想到不通過計算,畫圖也可以得出最便宜的方案。○表示一艘大船的價格,△表示一艘小船的價格,顯然有:○>△。全部租大船:32÷6=5(艘)……2(人),至多需要大船5+1=6(艘),用6 個○表示;5 艘大船和1 艘小船用5 個○、1 △個表示,下面類同,所有的方案表示如圖1:
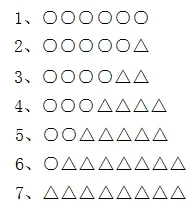
圖1
怎么比較它們的成本呢?我采用分組比較的方法,如圖2:

圖2
在每組中扣除相同的部分,又已知小船便宜,顯然,第一組中3便宜;第二組中5 便宜;第三組中7 便宜。因此只要比較3、5、7。
先比較5 和7:
我再想了一下,如果把題目的條件改一下變成“游客有33 人”會怎樣呢?顯然不可能沒有空位,因為游客是奇數,大小船載客都是偶數,那應該怎么辦呢?這樣一來,最省錢的方案應該是5 艘大船和1 艘小船(比4 艘大船和3 艘小船便宜)。為了研究一下這個結論是否正確,我繼續使用畫圖列表法,把所有可行方案都列出來,如圖3:
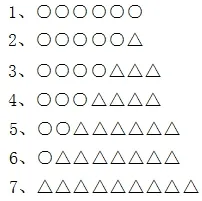
圖3
同樣進行分組比較(如圖4 所示):第一組中2 便宜;第二組中4 便宜;第三組中6 便宜。再比較2、4、6、7,顯然2 比4 便宜,4比6 便宜,6 比7 便宜,所以,最便宜的方案就是5 艘大船和1 艘小船。
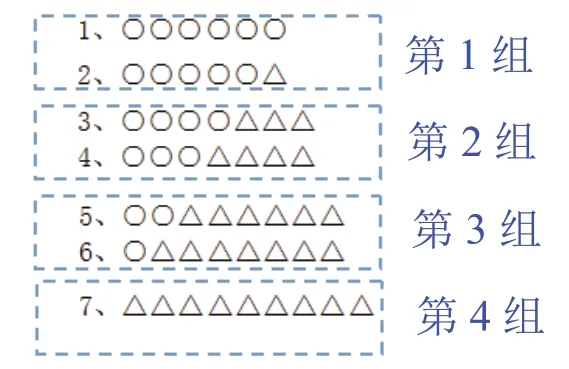
圖4
每一組去掉相同部分,可知第一組中2 便宜;第二組中4 便宜;第三組中6 便宜。再比較2、4、6、7,也可以得知:2 比4 便宜,4比6 便宜,6 比7 便宜,所以,最便宜的方案就是5 艘大船和1 艘小船。
接著,我又把課本題目的條件改了一下,游客還是32 人,但是小船的價格改為48 元,大船不變,這樣的話全部租大船反而是最便宜的了(雖然大船上留有空位),原來沒有空位的4 條大船和2 條小船反而不是最便宜的了。
看來,這種題目還是需要畫圖列表法才能篩選出最省錢的方案!但畫圖列表法本質上是窮舉,如果題目的數字很大就要花很多時間了。我研究了幾天,找到了一種改進的方法,我把它叫作“湊整替換法”。如課本上的題目條件不變,先考慮全部使用貴的小船,此時需要8 艘,然后把小船分組拼團,一組內小船的數量需要滿足能完整(不留空位)的用大船替換的條件(本質上是求大船載客數和小船載客數的最小公倍數),如題大船載客6 人,小船載客4 人,一個分組內的載客數就是12 人,此時需小船3 艘,能被2 艘大船完整替換。替換之后每組的成本肯定是降到最低的,只需要對最后余下來的人數進行列表法窮舉就行了,如圖5 所示:

圖5
對余下的2 艘小船(8 人)進行畫圖列表法窮舉,如圖6:

圖6
顯然,1是最便宜的方案。如果小船價格改為48元,就是3最便宜。如果人數改為33 人,價格不變,余下就是3 艘小船共9 人,這時2最省錢,也就是圖3 條件下得到5 艘大船和1 艘小船的方案。
一道簡單的數學課本題目,改動一個數據,參考量影響因子也會變化,所以對方法要理解到位,不能生搬硬套方法和結論。另外,一種分析策略也可以通過不斷優化,實現更簡潔的解題方法和思考過程。

