顧及系統間偏差的BDS/GPS單鐘差定位法
王彥恒,潘樹國,喻國榮,張 建
(1.東南大學 儀器科學與工程學院,江蘇 南京 210096;2.東南大學 交通學院,江蘇 南京 210096)
目前,多GNSS(Global Navigation Satellite System)偽距單點定位已廣泛應用于導航領域,但是,由于各系統接收機端硬件延遲不一致且難以與接收機鐘差分離[1-2],導致即使采用同一個接收機時鐘,對每個系統單獨考慮接收機鐘差項(本文稱之為傳統方法),使得冗余觀測量減少,數學模型強度降低,尤其在遮擋環境下,即使多系統存在因衛星過少參數過多而導致定位結果不可靠的問題。一個典型的情況就是當某個系統只觀測到1顆衛星時,由于吸收接收機端硬件延遲的接收機鐘差參數的存在,該系統并未提供冗余觀測信息[3]。而目前處于大眾消費水平的導航設備均采用傳統方法進行定位解算。
為了得到系統間偏差(ISB,Inter-System Bias)信息,需估計一個接收機鐘差參數(本文稱之為單鐘差模型),增加冗余觀測量,提高數學模型強度。但是,在導航中,從外部機構實時獲取所用設備的ISB信息比較困難,因此,需要依賴接收機硬件延遲的時域變化特性進行實時處理。
文獻[1]指出GPS硬件延遲較為穩定,對于與時間存在系統相關的硬件延遲,可采用簡單的線性模型進行逼近。文獻[4-7]的研究結果表明,GPS系統接收機端硬件延遲具有短期時域穩定性,日穩定度可優于1 ns。文獻[8-10]指出,北斗系統接收機端硬件延遲同樣具有時域穩定性。而對于BDS/GPS系統間偏差,理論上應處于短期穩定狀態,但是系統之間的相互影響可能會破壞穩定狀態;有學者研究表明,BDS/GPS系統間偏差同樣處于短期穩定狀態。文獻[3]利用BDS/GPS系統間偏差的時域穩定特性,進行BDS/GPS雙系統緊組合載波差分定位,結果表明,這種方式可以顯著增強遮擋環境下的定位精度與可用性,但是其采用的載波差分形式并不適用于目前普遍基于偽距進行定位的導航型終端。
利用ISB的時域穩定特性,在衛星數足夠的情況下,實時估計每個系統含有硬件延遲的接收機鐘差,從而獲得ISB信息,當進入遮擋環境,衛星數過少時,將已獲得的ISB信息當作已知量,從而減少待估參數,增加冗余觀測信息,增強數學模型強度,提高定位精度與可靠性,同時可以降低矩陣求逆維數,減少計算量。
基于目前導航終端所存在的不足與ISB的時域穩定性,本文提出單鐘差模型定位算法。采用實測數據驗證BDS/GPS雙系統在開闊環境及遮擋環境下單鐘差模型算法的可用性,并與傳統方法進行對比。
1 單鐘差模型及算法
BDS與GPS偽距觀測方程:
(1)
(2)
式中:P為偽距觀測值,上標s為衛星,下標B與G分別為BDS與GPS,下標r為接收機,ρ為站星距,T為對流層延遲,I為電離層延遲,dt為鐘差,hd為硬件延遲,ε為觀測噪聲。衛星鐘差與衛星端硬件延遲采用廣播星歷中的參數進行改正。
從式(1)與式(2)可以看出,若BDS與GPS共用同一個接收機時鐘,則只含有一個接收機鐘差項,但是由于接收機硬件延遲與接收機鐘差線性相關,難以分離,因此在傳統方法中,對BDS與GPS各引入一個接收鐘差參數,用以吸收硬件延遲,則式(1)與式(2)變形后:
(3)
(4)
其中:
dtr,B=dtr+hdr,B,dtr,G=dtr+hdr,G.
設共觀測到m顆BDS衛星與n顆GPS衛星,則誤差方程組:
(5)
式中:v為觀測值殘差;l,q,w為方向余弦;f為觀測信息;X,Y,Z為位置參數。假設事先獲得了BDS/GPS接收機端的ISB信息ISBB,G,ISBB,G計算方式:
ISBB,G=hdr,G-hdr,B=dtr,G-dtr,B,
(6)
聯合式(4)與式(6)可得:
(7)
則根據式(3)與式(7)所得誤差方程組:
(8)
比較式(5)與式(8)可知,在BDS/GPS雙系偽距單點定位中,若事先獲得接收機端的ISBB,G,則可減少一個接收機鐘差參數,提高數學模型強度。實際應用中從外部機構實時獲取所用設備的ISBB,G比較困難,但是可以利用ISBB,G的時域穩定特性,在衛星數足夠的情況下,采用傳統方法對BDS與GPS各估計一個接收機鐘差,按照式(6)得到ISBB,G,當衛星數較少時,將ISBB,G作為已知信息帶入觀測方程組,從而減少參數個數,提高數學模型強度。
2 實驗驗證與討論
采用兩組數據對單鐘差模型算法進行驗證,一組采用TrimbleNetR9數據,另一組采用UBLOX M8T數據,兩組數據信息如表1所示。

表1 實驗數據信息表
2.1 系統間偏差計算與分析
在進行單鐘差模型定位之前,首先分析在實驗數據時長內ISBB,G的時域穩定特性。先利用傳統方法估計BDS與GPS接收機鐘差,再利用式(6)計算ISBB,G,所得ISBB,G如圖1所示,圖1(a)與圖1(c)分別表示Trimble NetR9ISBB,G與ISBB,G的歷元間差分ΔISBB,G(t,t+1)(其中,ΔISBB,G(t,t+1)=ISBB,G(t+1)-ISBB,G(t))的變化趨勢,圖1(b)與圖1(d)分別表示UBLOX M8T的ISBB,G與ΔISBB,G(t,t+1)的變化趨勢,統計結果如表2所示。

表2 BDS/GPS系統間偏差統計表 m
注:表中ΔISBB,G(t,t+1)的MAX值采用絕對值計算
從圖1(a)與圖1(c)可以看出,Trimble NetR9在100 min內ISBB,G處于穩定狀態,從表2統計結果可以看出,ISBB,G穩定度為0.135 m,最大最小差為0.904 m,ΔISBB,G(t,t+1)RMS為0.077 m,歷元間差值最大為0.555 m,對于偽距單點定位米級定位精度而言,能夠保證在數分鐘之內將利用傳統方法獲得的ISBB,G作為已知信息進行單鐘差模型解算而并不明顯損失定位精度。
但是,Trimble NetR9接收機成本高,難以進入大眾導航領域,因此本文又選取成本較低的UBLOX M8T接收機進行實驗,其ISBB,G與ΔISBB,G(t,t+1)如圖1(b)與圖1(d)所示,統計結果如表2所示,綜合圖1(b)、圖1(d)與表2,UBLOX M8T接收機ISBB,G在100 min內較為穩定,穩定度為0.218 m,最大最小差為1.217 m,ΔISBB,G(t,t+1)的RMS為0.077 m,最大為0.365 m,同樣能夠保證在數分鐘之內將利用傳統方法獲得的ISBB,G作為已知信息進行單鐘差模型解算而并不明顯損失定位精度。
2.2 單鐘差模型驗證與分析
對ISBB,G時域穩定特性進行了分析之后,利用上述兩組數據對單鐘差模型定位效果進行驗證。在單鐘差模型定位中,每隔5 min利用傳統方法對ISBB,G進行更新;截止高度角分別設置為10°,30°,50°,其中30°和50°用來模擬遮擋環境;在對ISBB,G進行更新時刻,將截止高度角設置為10°。定位結果如圖2與圖3所示,圖2表示Trimble NetR9,圖3表示UBLOX M8T。從左至右依次為傳統方法定位偏差、單鐘差模型定位偏差、衛星數,從上至下依次為截止高度角10°,30°,50°。統計結果如表3所示。
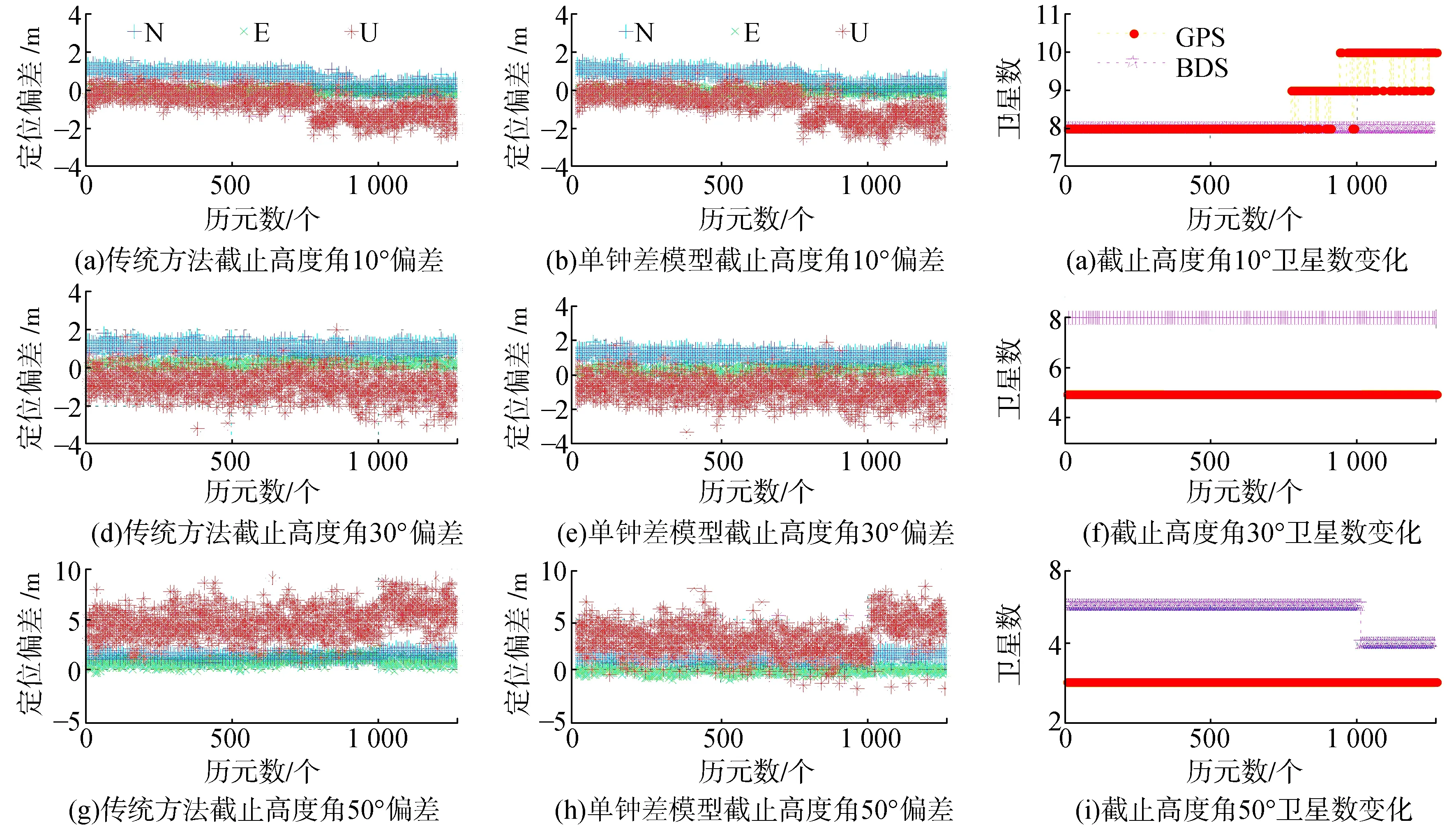
圖2 Trimble NetR9定位偏差
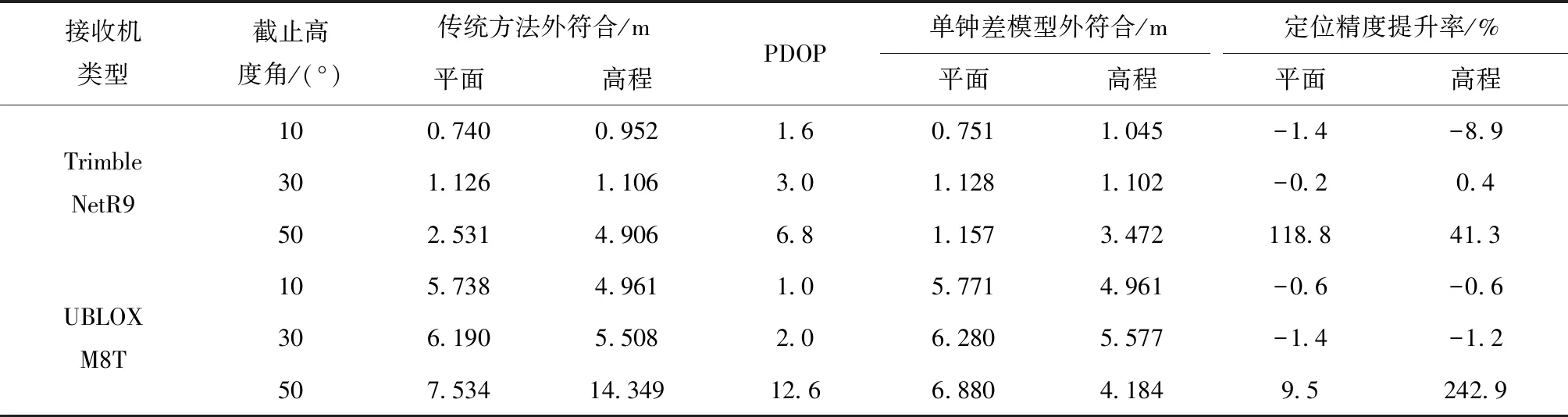
表3 定位結果對比統計表
從圖2、圖3及表3可以看出,在截止高度角分別為10°與30°時,單鐘差模型略低于傳統方法,這是因為衛星數足夠多,衛星幾何分布較好。當截止高度角提高到50°時,衛星數減少,幾何分布結構變差,數學模型強度過弱,單鐘差模型定位效果相對于傳統方法有明顯提升。Trimble NetR9在平面方向提升118.8%(1.374 m),高程方向提升41.3%(1.434 m);UBLOX M8T 平面方向提升9.5%(0.654 m),高程方向提升242.9%(10.165 m)。
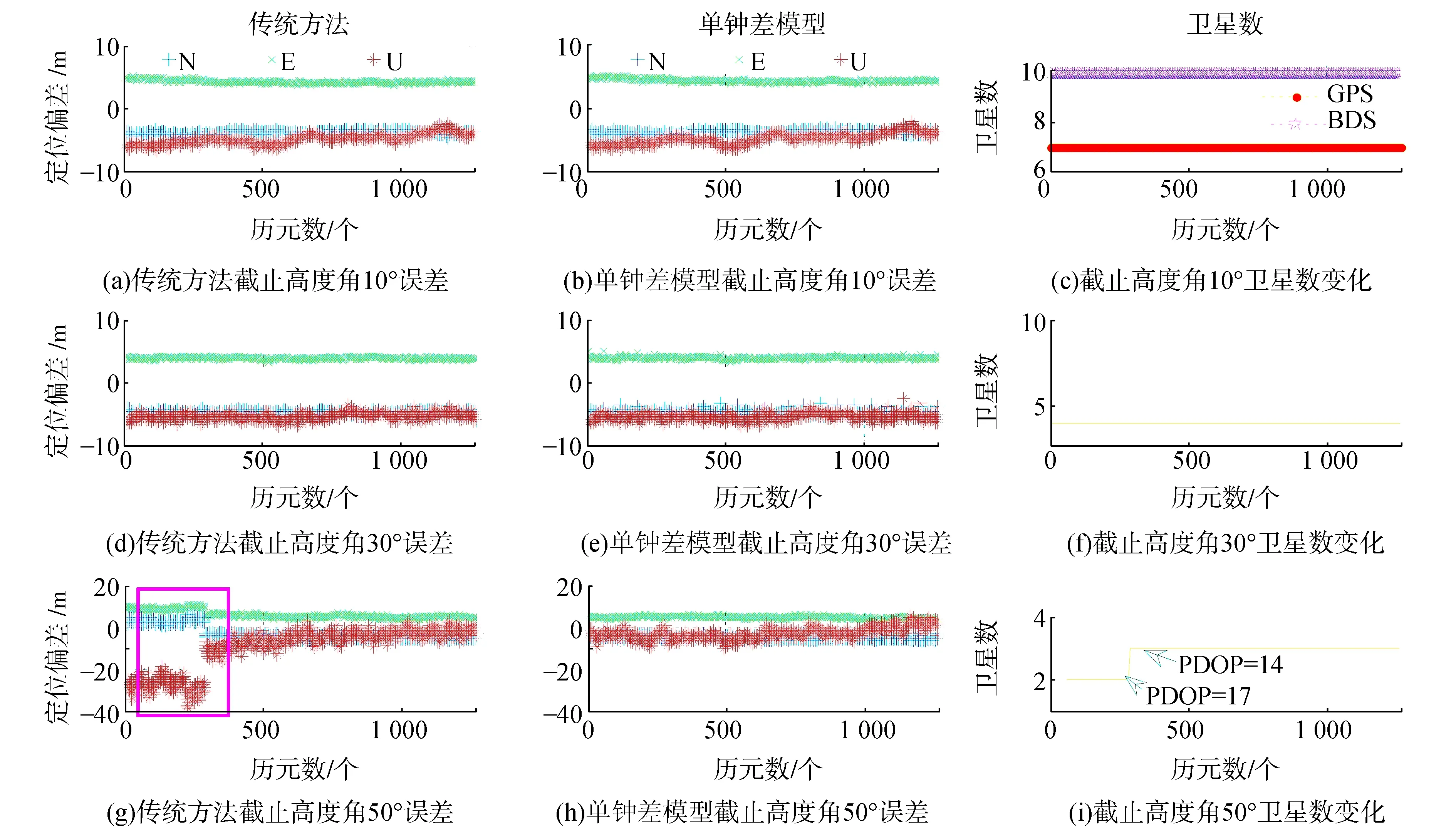
圖3 UBLOX M8T定位偏差

表4 衛星過少時定位結果對比統計表
從表4可知,UBLOX M8T在衛星數過少時,相對于傳統方法,單鐘差模型定位效果有明顯提升。其中,平面方向提升42.2%(2.707 m),高程方向提升500.4%(23.287 m)。
綜合圖2、圖3、表3與表4,相對于傳統方法,單鐘差模型在衛星數過少時能夠明顯提升定位效果,同時可以降低矩陣求逆維數,減少計算量。
3 結 論
本文研究一種顧及接收機ISB時域穩定特性的單鐘差模型定位算法。該算法首先在衛星數足夠的情況下對每個系統均引入一個接收機鐘差參數,獲取ISB信息,當進入遮擋環境,衛星數較少時,將前述所得ISB作為已知信息,以減少鐘差參數,提高數學模型強度,從而提高定位精度與可靠性,并能夠降低矩陣求逆維數,減少計算量。
為驗證算法的可行性并顧及大眾消費水平,共選取Trimble NetR9 與 UBLOX M8T 兩種接收機數據進行驗證。首先分析BDS/GPS系統間偏差的時域穩定特性,系統間偏差在100 min的穩定度分別為0.135 m和0.218 m,在數分鐘內能夠滿足單鐘差模型定位對系統間偏差穩定性的要求。接著對比傳統方法與單鐘差模型的定位效果,結果表明,在衛星數較少的情況下,單鐘差模型能夠顯著增強定位效果。相較于傳統方法,單鐘差模型能夠更好地應用于導航領域。
實際上,單鐘差模型定位算法在多系統聯合定位中效果提升會更明顯,例如在BDS/GPS /GLONASS/GALILEO 四系統定位中,相比于傳統方法可以減少3個鐘差參數,多提供3個冗余觀測量, 將矩陣求逆維數從7維降至4維,減少計算量,這也是本文下一步將研究的內容。

