單元復習課教學中存在的問題與建議
——以《數列》單元復習為例

丁益民

江蘇省蘇州實驗中學 (215011)

最近，筆者參與了我區招師活動的課堂教學考核環節，教學內容為蘇教版·必修5教材(下稱教材)數列單元復習課，從參與應聘的30位教師的課堂展示情況來看，發現很多教師并沒有準確認識單元復習課的教學功能.為什么要上單元復習課？學習論認為，經過一階段的新課學習，學生獲得的是一些簡單概念和單一的解題技巧，對這些零散的點狀知識容易產生遺忘和混淆.因此，需要對已學知識進行梳理與整合，單元復習是將本單元的相關知識進行梳理、歸類、鞏固，理清知識間的邏輯關聯，構建出系統的知識網絡，從單元的角度理解數學知識.

一、單元復習課教學中的存在問題

從應聘教師的課堂展示可以看出當前有些教師對單元復習課的課型功能認識并不準確，或上成知識羅列課，或上成解題教學課，或上成專題復習課，給人一種簡單堆砌、偏離目標之感.主要存在以下問題：

問題1 教學達成目標的層次偏低

一些教師在制定單元復習課的教學目標時，簡單地將本單元各課時目標進行匯總，更多關注知識點的“全”，卻不能整合知識點間的邏輯要素，導致單元復習成了一種“炒冷飯”式的知識點回顧，課堂教學始終在低位目標徘徊.

很多教師在知識回顧時都采用“數列的定義→數列的通項公式→等差數列的通項與求和→等比數列的通項與求和”的復習線路，這樣的過程就是單純地按照知識順序進行無意義的回顧，并不能幫助學生形成上位的整體認知，這樣復習的效果自然不夠理想.實際上，根據學生已有的認知，提煉出知識間的邏輯主線，將整章內容串聯到這樣的邏輯主線中去，從整體上形成知識的邏輯架構.

問題2 教學處理的深度不夠

有些教師在單元復習時中只關注識記性知識和程序性知識目標的落實，卻對基本數學活動經驗的構建、重現以及關鍵能力的培養不予重視，導致課堂教學的深度不夠.

如有些老師都選擇教材P68第12題作為“錯位相減法”的復習載體：

題目 已知等差數列{an}滿足a2=0,a6+a8=-10.

(1)求數列{an}的通項公式；

絕大部分老師是這樣處理的：引導學生分析問題(2)中的處理方法(錯位相減法)后口頭強調該法容易出錯，卻鮮有老師將本題的完整過程重現出來.學生在沒有切身體驗下的認知是不深刻的，口頭強調式的教學手段并不能強化學生認知結構中的活動經驗.

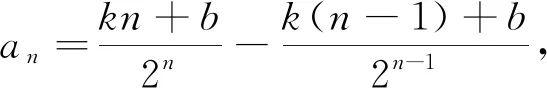
問題3 組織方式比較低效

單元復習課中常見的教學組織方式有兩種：一是講知識點為主，把本單元所有知識點羅列在一起，重新再講一遍，這種直敘式的組織形式讓學生覺得索然無趣，效果可想而知；二是講題為主，根據本單元知識點選擇一些習題讓學生練習后再講評，這種組織形式沒有依據學生的實際認知，復習并沒有針對性.

師1的組織方式：

習題1：……知識點撥1：……

習題2：……知識點撥2：……

師2的組織方式：

知識提要1：…… 習題1：……

知識提要2：…… 習題2：……

以上兩位老師的教學組織都沒有關注知識、能力與經驗的內在關聯，無助于學生構建單元的知識、思維能力和數學活動經驗體系.其實，可以將上述教學組織中“知識點撥”、“知識提要”設計為“知識梳理”，再引導學生獨立完成、交流完善，從中體現習題間的邏輯關聯和層次性.

二、單元復習課的教學建議

1.準確認識“本章回顧”的設置意圖

為了減少單元復習的隨意性和盲目性，教材在每章末都設置了“本章回顧”.主要包括：知識結構，學習要求(包括知識、技能、思想方法)以及內容提要.在知識結構的呈現方式上采用的是框圖形式，直觀形象地反映了知識的來龍去脈，并且框圖可以進一步開發整合(比如常可拓展成思維導圖).學習要求不同于課時要求，是對整個單元的宏觀要求，內容提要則采用提綱形式將本章主要內容予以回顧，目的是抓住主干知識，舍末求本，其目的是防止擴張教學范圍，杜絕深挖教學內容，這是單元復習的行動綱領.

就“數列”一章而言，在復習時應引導學生從兩個認知視角進行梳理，一是函數視角，數列是以“數”為研究對象的特殊函數，整個數列教學體系中，應始終以函數的視角來審視數列的性質，比如數列中的項是如何變化的(如單調性)？數列的項與項之間有怎樣的關系(遞推關系)？等等.另一個是運算視角，即建構合適的運算規則來研究數列中的運算，比如，通過“累加”的運算方式得到等差數列的通項公式，進一步地這樣的運算規則還適用于形如遞推關系“an-an-1=f(n)”的通項公式求解問題.以這兩條線索可進行以下梳理：

函數視角

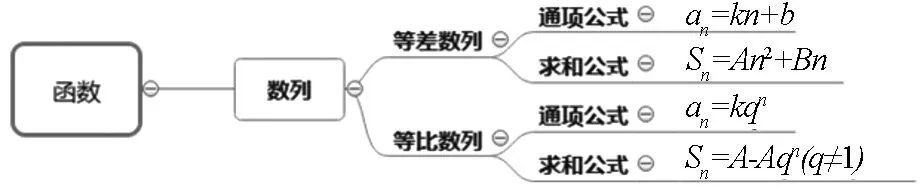
運算視角

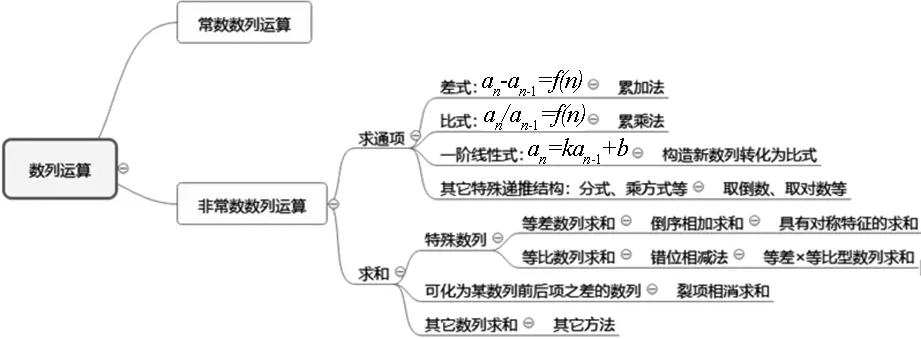
通過從這兩條認知視角來整合已學內容，形成新的認知塊，加深知識的關系系理解，促進深度理解.

2.實施有效的教學組織

教學組織方式決定了單元復習的質量，單一羅列知識和逐一講解例題的實際教學效果往往高耗低效，學生的數學理解水平淹沒在題海之中.在復習時可以圍繞核心概念展開，引導學生運用已有知識來論證核心概念；或者尋找支撐核心概念的一般概念與相關具體問題，試圖對原有知識進行必要的拓展與深化，建立起知識間的邏輯聯系，并確定知識的運用范圍，實現知識的深度理解.

導學模式是進行單元復習時十分有效的組織形式之一，將復習內容以問題的形式呈現出來，問題可由學生先行解決.問題設計時要關注問題的起點、層次與跨度，起點不宜太高，適當高于新授課要求，逐層推進，思維跨度不宜太大，要具有一定的啟發性與針對性，通過問題鏈著力構建出完整的知識框架.

要提高學生在解決問題時目標任務的達成度和效度.在“前置練習”中設置有關核心概念、重要性質的基礎題，通過前置練習梳理出相關概念與性質，進而拓展出與之相關的外延知識.在此過程中那些無關緊要的知識堅決舍去(如等差數列的某些識記性的結論)，抓住重點，擯棄雜質，太多太空的結論性知識易將學生帶入務虛空洞的知識梳理，這樣就成了無意義的數學活動.梳理出的知識應與選擇的例題相匹配，例題講評的目的是加深核心知識的理解.最后再對整節課的進行小結.所以，整節課就是核心概念主線下進行的教學組織.

3.精心選編適合學生的典型例題

單元復習課離不開例題的選擇與講評，很多老師在單元復習時完全照搬高三復習資料中的成品例題，這就導致教學起點過高，教學難度過大，發生了教學重心偏移，起不到應有的復習效果.因此，在選題時要有一定的針對性、適度性和思考性.實際上，教材中有很多典型且適合學生認知特點的典型例題，可以借助這些例題進行復習提升.

如教材P68第17題：在等差數列{an}中，已知Sp=q,Sq=p,(p≠q)，求Sp+q的值.

很多老師在講評此問題時僅僅將之定位成一個“結論”讓學生記住，其實這道題的教學功能很多.

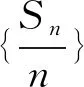
由此可見，選擇合適的例題并從整體性中尋找問題解決的要素，對學生的思維訓練與能力提升是有益的.

單元復習課教學研究任重道遠，針對不同的知識類型，不同的學生群體，探索出適合的單元復習課教學模式和教學策略，提高單元復習課的教學深度，促進學生思維水平的發展和知識的理解深度.