一道高考題求解錯誤的調查研究

賈麗紅

甘肅省蘭州市第二十七中學 (730030) 陳鴻斌甘肅省蘭州市第五十二中學 (730000)

筆者對一道2017年高考文科數學全國卷Ⅰ第17題進行了調查研究,驚訝的發現了學生的7類求解錯誤,同時也發現了學生的幾種巧妙解法.通過調查研究,反思我們高三復習以及高中數學教學中的不足與缺陷,并提出一些改進措施：重視數學核心素養的發展；注重數學思想方法的滲透；用正確的方法糾錯；培養良好的非智力因素.

1 問題的提出

研究高考題一直以來是一個熱門話題,一道好的高考題凝聚著專家們的智慧和心血,它可以反映出學生學習中的很多問題，而糾錯、改錯在高三復習中是非常重要的,讓學生在糾錯、改錯中不斷成長,逐步培養他們的數學核心素養,同時啟發我們平時命題的針對性.

2 研究過程

2.1 調查對象

調查對象為甘肅省蘭州市市屬學校2019屆的163名在校高三文科學生.

2.2 調查方法

采用試卷調查法和訪談法.收集試卷150份,選擇其中25名學生進行訪談.

3.研究結果與分析

3.1 試題呈現

題目(2017·文科全國卷Ⅰ)記Sn為等比數列{an}的前n項和,已知S2=2,S3=-6.

(1)求{an}的通項公式;

(2)求Sn,并判斷Sn+1,Sn,Sn+2是否成等差數列.

本題的正確率很低,只有6%的同學完全解得答案,還有5%的學生干脆沒有解答,是由于本身基礎太弱,無從下手.可見,全國卷Ⅰ對于一直使用全國卷Ⅱ的甘肅考生來說,確實比較難.

3.2 誤區分析

經過統計,錯誤類型調查結果如下表.

錯誤類型錯誤一錯誤二錯誤三錯誤四錯誤五錯誤六錯誤七百分比5%10%30%2%5%34%20%

由上表可見，學生對此問題的解答錯誤率很高，對此我們分析求解錯誤的原因.

錯誤一:審題不清而致錯

5%的學生審題不清,錯誤的將等比數列看成了等差數列,暴露出這部分學生沒有養成良好的解題習慣,粗枝大葉、心浮氣躁而不仔細審題.

錯誤二:目標不明確，不知求解哪些量

10%的學生不知道求等比數列通項公式,需要確定哪些量.暴露出這部分學生公式記憶不清晰,沒有理解等比數列通項公式an=a1qn-1需要確定a1和q,也沒有內化方程的思想.

錯誤三:不會消元求解方程組

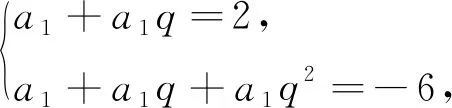
錯誤四:分式約分錯誤

2%的學生能夠想到除法消元,可是分式約分錯誤,學生的錯誤解答如下:

以上解答暴露出這部分學生不明白分式約分的法則,約去的是一個分子、分母的非零公因子,說明數學基礎不扎實.

錯誤五:一元二次方程的根解錯

錯誤六:將(-2)n運算成-2n而致錯

有高達34%的學生犯了此類錯誤,其中一部分同學是書寫習慣不好,沒有加括號的意識;另一部分則是錯誤地認為(-2)n=-2n.暴露出的問題是學生學習數學的態度與習慣,還有不能區分(-2)n和-2n.

錯誤七:不會化簡(-2)n+2+(-2)n+3

3%的學生對于(-2)n+2+(-2)n+3的化簡,與同底數冪的乘法法則混淆而化成了(-2)2n+5.暴露出此類學生運算能力較弱,以及做題時復雜多變的心理.

3.3 問題分析

從學生的解答來看,做對的學生目標明確,基本功扎實,數學核心素養好,解法多樣,簡潔有效.

q2+4q+4=0.解得q=-2,將q=-2代入a1+a1q=2,得a1=-2.所以an=(-2)n.

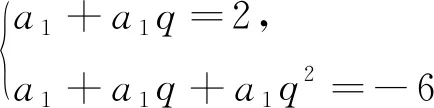
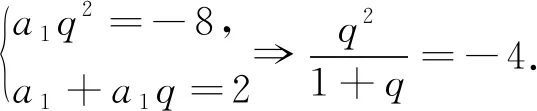
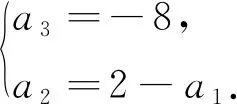
從解法三看出,這些學生對等比數列已經熟練掌握,不但可以簡化表達,而且還能熟練應用等比中項解決問題.這些學生在學習中能夠自主探究和歸納總結,具有良好的思維品質.以上三種解法都體現著方程的數學思想,核心素養之數學運算是求得正解的支撐.

所以Sn-Sn+1=Sn+2-Sn.故Sn+1,Sn,Sn+2成等差數列.

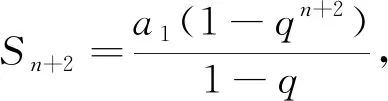
解法一、解法二主要是同底數加減法的運算,須具備數學運算的核心素養；解法三、解法四利用數學公式進行推理,排除了(-2)n帶來的困擾,抓住問題的核心,進而優化了解題思路,須具備數學抽象和邏輯推理的核心素養才能實現,同時體現了劃歸與轉化的數學思想、函數與方程的數學思想.尤其是解法四,從Sn+1,Sn,Sn+2之間的關系入手,使運算更加簡潔、明了.

4.結論與建議

4.1 結論

通過調查筆者發現,文科學生的求解錯誤最多的是來自知識本身沒理解、數學運算帶來的;其次是思維能力和審題不清等導致的錯誤類型,對于文科生來說,數學核心素養是有限的,而數學核心素養的培養是一項工程.相對而言,審題不清的致錯原因很少,主要是因為本題難度相對較大,數學核心素養的要求很高所致,這也說明學生綜合解決問題的能力有限.

4.2 建議

(1)重視數學核心素養的發展

高考以能力立意,全面考查體現數學學科特點的六大核心素養,即數學抽象、邏輯推理、數學建模、數學運算、直觀想象、數據分析.而良好的數學核心素養則是需要經過多次反復,從實踐中鍛煉出來的.這樣通過發散思維訓練,突破固定的思維模式,逐步培養學生的數學核心素養.

(2)注重數學思想方法的滲透

高中階段主要掌握七大數學思想方法,即函數與方程的數學思想、數形結合的數學思想、分類與整合的數學思想、化歸與轉化的數學思想、特殊與一般的數學思想、有限與無限的數學思想、或然與必然的數學思想,其中在高考中,函數與方程的數學思想方法、數形結合的數學思想方法、化歸與轉化的數學思想方法體現得最為突出．因此,在高三復習中要非常注重滲透數學思想方法,從而可以優化解題思路,找到合理的突破口,減少求解錯誤的發生.

(3)用正確的方法糾錯

認真分析求解錯誤的成因,針對不同的錯誤類型,進行易錯題歸類、總結,以便于學生對知識的再認識.

(4)培養良好的非智力因素

有時候學生的許多解題錯誤與非智力因素也是離不開的,應在糾正不良的心理品質上下功夫.如要求學生上課時要專心致志,注意力集中；要有克服困難的精神,不能知難而退；克服馬虎、粗心、不認真檢查的毛病；并教育學生樹立學習的信心,有助于提高成績.