強(qiáng)化運(yùn)算素養(yǎng) 提升思維品質(zhì)*
——以橢圓中的運(yùn)算為例

高新檸 郭建華(指導(dǎo)教師)

江蘇省南京市第二十九中學(xué) (210036)

解析幾何的運(yùn)算給人們的感覺是繁瑣，有的同學(xué)遇到解析幾何問題就會感到畏懼，不敢去算，也不愿意去算，或者是沒有掌握運(yùn)算的技巧和方法，算不下去，于是導(dǎo)致解析幾何題得分較低，因此，很有必要在平時的訓(xùn)練中加強(qiáng)對解析幾何題的各種題型進(jìn)行歸類和反思.尤其對解析幾何題要在運(yùn)算上多下功夫，因?yàn)樗墙鉀Q問題的基本手段.其實(shí)數(shù)學(xué)運(yùn)算主要表現(xiàn)以下四個方面：理解運(yùn)算對象，掌握運(yùn)算法則，探究運(yùn)算思路，求得運(yùn)算結(jié)果.通過橢圓中運(yùn)算的培養(yǎng)，進(jìn)一步發(fā)展數(shù)學(xué)運(yùn)算能力，不斷促進(jìn)數(shù)學(xué)思維的發(fā)展，提升規(guī)范化思考問題的品質(zhì).下面通過例題淺談一下解析幾何運(yùn)算中思維品質(zhì)的提升.

1.理解運(yùn)算對象，提升思維的敏捷性

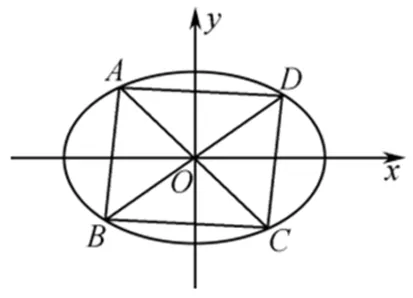
圖1

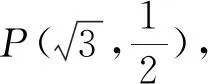
(1)求橢圓T的方程；

2.探究運(yùn)算思路，激活思維的靈活性

圖2

證明：(方法1) 設(shè)直線A1M的方程為y=k1(x+2)，直線A2N的方程為y=k2(x-2)．聯(lián)立方程組

下面證明對于任意的實(shí)數(shù)m，直線A1M與直線A2N的交點(diǎn)G均在直線x=4上．

點(diǎn)評:思維的靈活性是指思維活動的靈活程度，善于根據(jù)事物的發(fā)展變化，及時地用新的觀點(diǎn)看待已經(jīng)變化了的事物，并提出符合實(shí)際的解決問題的新設(shè)想、新方案和新方法.也就是能從不同角度觀察、不同層次思考、利用不同方法依據(jù)新的條件迅速確定探究運(yùn)算思路，探尋解決問題的最優(yōu)方案.證明思路1通過設(shè)直線A1M與直線A2N的方程求解點(diǎn)M,N的坐標(biāo)，再利用M、D、N三點(diǎn)共線找出k2,k1關(guān)系，從而得證，在運(yùn)算上較為繁瑣；由于要證明的目標(biāo)很明確，因此思路2選擇特殊法處理，其實(shí)這是優(yōu)先考慮的一種解法.另外根據(jù)直線MN過x軸上的定點(diǎn)，設(shè)其方程為x=my+1，這樣不僅提高了解題的速度和準(zhǔn)確度，而且降低了思維的難度.在橢圓的運(yùn)算中要從不同角度分析問題，加強(qiáng)解題方法的對比，才能探尋到更好的求解方案，更有利于培養(yǎng)思維的靈活性.

3.選擇運(yùn)算方法，培養(yǎng)思維的獨(dú)創(chuàng)性

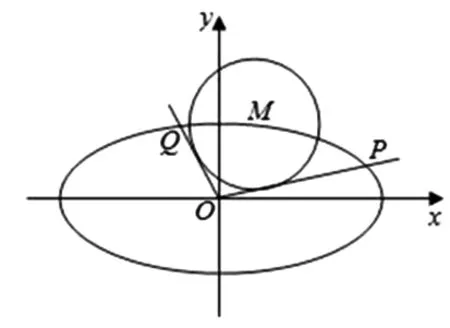
圖3

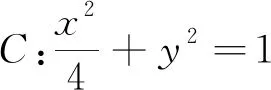
(2)求OP·OQ的最大值．

(2)設(shè)P(x1,y1),Q(x2,y2)，聯(lián)立

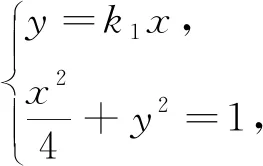
算法1 由于目標(biāo)函數(shù)為齊次式，先將其進(jìn)行常數(shù)分離，再用基本不等式求解.

算法2 利用換元法，再結(jié)合二次函數(shù)求解.

算法3 通過分析、觀察分式目標(biāo)函數(shù)的結(jié)構(gòu)，對分子用基本不等式求解即可.

算法4 采用先特殊后一般的方法，再結(jié)合基本不等式求解.

(1)當(dāng)直線落在坐標(biāo)軸上時，顯然有OP2+OQ2=5；

點(diǎn)評:算法1和算法2都是常規(guī)方法，運(yùn)算較煩，算法3最簡潔，需要很強(qiáng)的觀察力，算法4先特殊后一般，也是處理解析幾何的常用方法.橢圓中分式求最值問題是很繁瑣的，要想更快的求得運(yùn)算結(jié)果，必須學(xué)會選擇最優(yōu)的運(yùn)算方法，在方法的選擇和比較中會不斷的發(fā)現(xiàn)問題、提出問題，才會在解題中養(yǎng)成更全面、深刻、完整的思考問題的習(xí)慣，才會在新情景中采取新對策培養(yǎng)分析問題和獨(dú)立解決問題能力，進(jìn)而培養(yǎng)思維的獨(dú)創(chuàng)性.

4.求得運(yùn)算結(jié)果，提升思維的深刻性

點(diǎn)評:思維的深刻性是指能深入到事物的本質(zhì)里去考慮問題，它是以思維的批判性為前提的.三角形內(nèi)角平分線的性質(zhì)是本題考察的核心，也是求解該問題的切入點(diǎn)，也為在關(guān)聯(lián)的情景中準(zhǔn)確確定運(yùn)算對象，運(yùn)算法則和明確運(yùn)算方向提供前提.解法1是利用其對稱性求解，運(yùn)算繁瑣，解法2是在綜合情景中聯(lián)想到光學(xué)性質(zhì)求解，利用橢圓的切線方程迅速求得結(jié)果，解法3借助于焦半徑和角平分性質(zhì)求解也是一個很好的選擇，在求得運(yùn)算結(jié)果的過程中，加深問題的深刻理解，把握問題的本質(zhì)內(nèi)涵，選擇靈活的方法，發(fā)散思維，讓思維在解題中真正發(fā)揮作用.

總之，在處理橢圓的典型運(yùn)算問題時，不僅要掌握算法，而且要明白算理，在運(yùn)算上多下功夫，對一道典型的問題要深入研究，探究解法的多樣性，加強(qiáng)運(yùn)算素養(yǎng)的培養(yǎng)，從而提升思維的品質(zhì).