基于非線性動態(tài)規(guī)劃的波多黎各颶風(fēng)災(zāi)難救援模型研究

劉越 王志堅

摘 要：本文研究了救援響應(yīng)系統(tǒng)開發(fā)，在裝箱問題上面對客觀約束采用非線性規(guī)劃模型，在空間利用率達(dá)到最大化的目標(biāo)函數(shù)下，對貨物的數(shù)量、旋轉(zhuǎn)方向、體積和承載重量做出約束，再使用動態(tài)規(guī)劃模型確定裝箱方案。在配送集裝箱時分3種情況構(gòu)造模型，分為停靠1個、2個和3個港口，遍歷港口與5個醫(yī)療包交貨地點(diǎn)間的距離并篩選得到最小距離求得對應(yīng)的停靠港口。

關(guān)鍵詞：非線性規(guī)劃；動態(tài)規(guī)劃；遍歷

很多學(xué)者研究過三維裝箱問題及最佳分配問題。本文研究的是相同尺寸物品裝箱問題，通過構(gòu)造模型尋找最佳包裝配置，且綜合考慮救援效率及成本和其他客觀要求，結(jié)合實際情況為最佳包裝配置選取合適港口以便進(jìn)行組織的下一步營救。

1 研究背景

2017年美國波多黎各遭受當(dāng)?shù)厥飞献顕?yán)重颶風(fēng)，造成了嚴(yán)重破壞和重大人員傷亡。非政府組織HELP，Inc通過設(shè)計“DroneGo”可移動災(zāi)難響應(yīng)系統(tǒng)來提高其救援響應(yīng)能力。HELP，Inc已經(jīng)確定使用各種旋翼無人機(jī)來組成DroneGo車隊。為了增加受災(zāi)現(xiàn)場的援助用品，DroneGo準(zhǔn)備了三種醫(yī)療包MED1、MED2和MED3。無人機(jī)承擔(dān)運(yùn)輸醫(yī)療包的任務(wù)，可以通過外部貨艙運(yùn)輸多個醫(yī)療包。本文根據(jù)各營救點(diǎn)的需求及救援路線和偵查路線為HELP，Inc解決營救計劃的包裝配置和物資運(yùn)輸問題。結(jié)合波多黎各的颶風(fēng)災(zāi)難情景，為最多三個標(biāo)準(zhǔn)ISO集裝箱設(shè)計相關(guān)的包裝配置，形成HELP，Inc設(shè)計無人機(jī)隊和醫(yī)療包裝配方案。找到波多黎各的最佳位置，確定DroneGo災(zāi)難響應(yīng)系統(tǒng)一個或多個集裝箱位置，有利于提供醫(yī)療服務(wù)和道路視頻偵察。

2 裝箱問題與包裝配置

無論是醫(yī)療包放進(jìn)無人機(jī)外部貨艙和運(yùn)輸集裝箱，還是運(yùn)輸集裝箱放進(jìn)ISO集裝箱，都要與集裝箱邊線平行，即正交布局。

要求最多使用三個標(biāo)準(zhǔn)ISO集裝箱，本文運(yùn)用非線性規(guī)劃模型，把醫(yī)療包放入無人機(jī)的外部貨艙，將無人機(jī)和剩余醫(yī)療包放入運(yùn)輸集裝箱內(nèi)，再把運(yùn)輸集裝箱按數(shù)量最大限度地裝載進(jìn)標(biāo)準(zhǔn)ISO集裝箱，即研究三維裝箱問題，假設(shè)各種集裝箱和醫(yī)療包的形狀都是規(guī)則的長方形，它們的重心即其幾何中心，對此建立空間直角坐標(biāo)系。考慮目標(biāo)函數(shù)和現(xiàn)實約束，其中需要注意的是無人機(jī)的運(yùn)輸集裝箱只能正交旋轉(zhuǎn)90°，不能對任何運(yùn)輸物品進(jìn)行倒置或側(cè)放。

3 集裝箱停靠位置選取

裝載包裝配置后需要將標(biāo)準(zhǔn)ISO集裝箱進(jìn)行分配派送，需獲取1個、2個或3個最佳停靠位置。由于最多使用3個港口，故分3種情況構(gòu)造模型。

本文在GoogleMap上獲取波多黎各的11個主要港口的經(jīng)緯度。如下表所示：

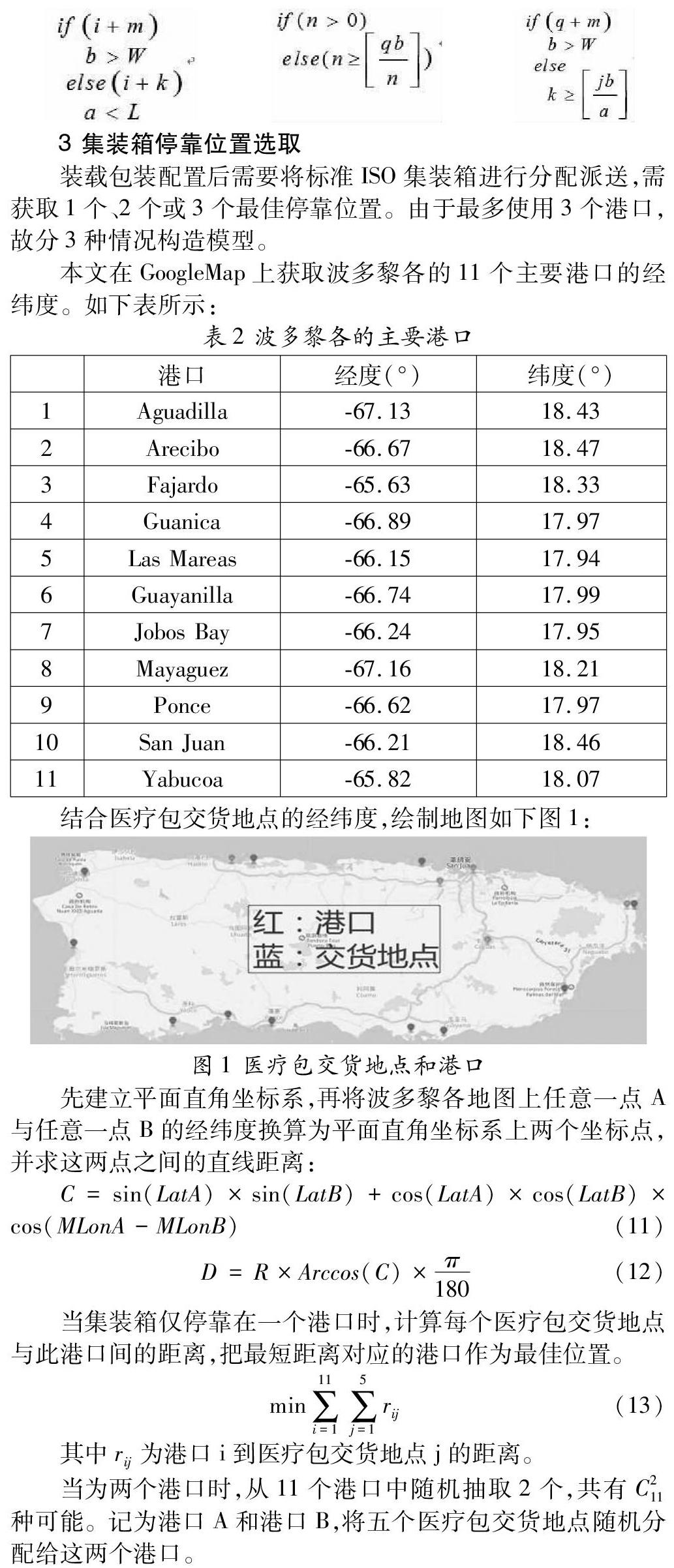
結(jié)合醫(yī)療包交貨地點(diǎn)的經(jīng)緯度，繪制地圖如下圖1：

先建立平面直角坐標(biāo)系，再將波多黎各地圖上任意一點(diǎn)A與任意一點(diǎn)B的經(jīng)緯度換算為平面直角坐標(biāo)系上兩個坐標(biāo)點(diǎn)，并求這兩點(diǎn)之間的直線距離：

當(dāng)集裝箱僅停靠在一個港口時，計算每個醫(yī)療包交貨地點(diǎn)與此港口間的距離，把最短距離對應(yīng)的港口作為最佳位置。

當(dāng)為兩個港口時，從11個港口中隨機(jī)抽取2個，共有C211種可能。記為港口A和港口B，將五個醫(yī)療包交貨地點(diǎn)隨機(jī)分配給這兩個港口。

其中港口A分得m個醫(yī)療包交貨地點(diǎn)，則港口B分得5-m個交貨地點(diǎn)（m=1，2，3，4）。計算港口與所分配交貨地點(diǎn)間的距離，求和得到分配方案總距離。通過遍歷方法篩選出多種分配方案總距離最小值，把該種方案對應(yīng)的兩個停靠港口視為最佳停靠位置。

當(dāng)標(biāo)準(zhǔn)ISO集裝箱停靠三個港口時，從11個港口中任意抽取三個港口，將5個醫(yī)療包交貨地點(diǎn)隨機(jī)分配給這三個港口。同理可得多種分配方案的總距離最小值，把該種方案確定的三個停靠港口視為最佳位置。

4 研究結(jié)論

對本文非線性規(guī)劃的約束條件和目標(biāo)函數(shù)使用python求解，得到結(jié)果如下：

本文為災(zāi)難響應(yīng)系統(tǒng)設(shè)置2臺E型無人機(jī)，1個H Tethered平臺，363個E型運(yùn)輸集裝箱，1個H型運(yùn)輸集裝箱和3個標(biāo)準(zhǔn)ISO集裝箱。其中會出現(xiàn)兩種裝載情況，第一種情況是用無人機(jī)外部攜帶的貨艙裝載醫(yī)療包，運(yùn)輸集裝箱裝載無人機(jī)；第二種情況是僅用運(yùn)輸集裝箱裝載醫(yī)療包。再把所有運(yùn)輸集裝箱放進(jìn)ISO集裝箱。

使用C++對包裝配置的動態(tài)規(guī)劃二維裝箱模型進(jìn)行裝載計算，其中兩個標(biāo)準(zhǔn)ISO集裝箱，一個內(nèi)部裝載126個E型運(yùn)輸集裝箱，空間利用率為85.1%。另一個裝載111個E型運(yùn)輸集裝箱和1個H型運(yùn)輸集裝箱，其中有兩個E型運(yùn)輸集裝箱裝載E型無人機(jī)，H型運(yùn)輸集裝箱裝載H Tethered平臺，空間利用率為85%。兩種裝箱方案的空間利用率較高，是可行的結(jié)果。其中醫(yī)療包放進(jìn)運(yùn)輸集裝箱的方法有兩種：第一種方法是3個MED1和3個MED3。第二種方法是4個MED1，2個MED2和3個MED3；且每一天所需醫(yī)療包的包裝量剛好滿足兩個E型運(yùn)輸集裝箱的最大承重能力，裝載后的剩余運(yùn)輸集裝箱底面面積相對較少。

在尋找最佳位置的模型中，通過python多次遍歷計算得到在3種情況中港口與醫(yī)療包交貨地點(diǎn)之間的距離，并自動篩選出之中的最短距離，其對應(yīng)的港口即為標(biāo)準(zhǔn)ISO集裝箱的最佳放置地點(diǎn)。求解得到結(jié)果如下：

參考文獻(xiàn)：

[1]許佳瑜.三維裝箱約束下的車輛路徑優(yōu)化研究[D].長安大學(xué)，2018.2.

[2]農(nóng)健恒.同尺寸物品裝箱的動態(tài)規(guī)劃算法[D].廣西大學(xué)，2014.

[3]鄭洪清.CS算法在應(yīng)急救援中最佳路徑的應(yīng)用研究[J].山東工業(yè)技術(shù)，2018（15）：241-242.

作者簡介：劉越（1997-），廣東潮陽人，2016級本科生，研究方向：應(yīng)用統(tǒng)計學(xué)；王志堅（1982-），江西余干人，博士，講師，研究方向：管理統(tǒng)計方法。