尾拋式救生艇兩種釋放過程的建模與分析
邱紹楊,譚家萬,任鴻翔,蔣效彬
(1. 大連海事大學 航海動態仿真和控制交通行業重點實驗室,遼寧 大連 116026;2. 重慶交通大學 航運與船舶工程學院,重慶 400074)
0 引 言
救生艇是船上主要救生設備之一。當海難事故發生時,船上人員可借助救生艇迅速地脫離難船。自由降落式救生艇出現后,經過百余年的優化和完善,其釋放方式和過程已經有別于傳統舷側降落的救生艇。將自由降落式救生艇安放于船尾,釋放操作簡單,由艇內操作人員打開釋放鉤即可完成釋放。在釋放過程中,艇體不會與母船發生碰撞,而且能夠迅速到達水面。因此,自由降落式救生艇已廣泛應用于海上救生撤離等場景中。
自由降落式救生艇具有兩種釋放方式:自由降落和吊放。基于此,筆者為自由降落過程中的救生艇運動建立了數學模型,為吊放過程中的吊艇臂和艇運動建立了數學模型,并將數學模型應用于船舶救生模擬訓練系統中,期望提高系統仿真精度。
對救生艇自由降落入水模型,國內研究較少,多采用計算流體力學軟件進行模擬。黃春平等[1]僅研究了救生艇入水過程中,救生艇與母船最大距離及入水深度;李艷臣等[2]利用動力分析軟件,對玻璃鋼救生艇入水過程進行了數值仿真,分析了拋落式玻璃鋼救生艇入水過程的船體應力分布情況。國外學者對此研究較多,V.KARMAN[3]提出并利用動量定理來解決入水沖擊問題;W.J.C.BOEF[4]、M.ARAI等[5]、A.OGAWA等[6]、M.R.H.KHONDOKER等[7]分別對救生艇自由降落入水模型進行了深入研究,并將該模型不斷簡化和完善;M.KARIM等[8]在前人研究基礎上充分考慮了規則波對救生艇入水時的影響。在吊放救生艇過程,需要對機械吊臂進行動力學分析,羅天洪等[9]提出基于變形旋量理論的工業機器人機械臂剛柔耦合動力學建模方法;殷時蓉等[10]利用牛頓-歐拉法建立了舉升臂的機構模型,在此基礎上對其舉升臂的作業過程進行了動態仿真分析;康碩[11]分析了艇與收放裝置在二自由度平面運動,利用拉格朗日方程建立模型;徐世鈺[12]、楊揚[13]、袁士杰[14]和劉巧伶[15]分別利用Kane方法對機械吊臂進行了建模,Kane方法不考慮理想約束,模型簡單,且易于理解。
筆者以實際尺寸救生艇為研究對象,建立了救生艇自由降落入水的運動模型,并根據動量理論和切片理論計算了救生艇入水時所受的流體力;計算救生艇入水速度時考慮了波面運動影響,并利用插值計算方法對救生艇橫截面半寬和入水時的附加質量進行計算;在計算附加質量時,考慮到橫剖面完全浸入水情況,分別對滑道傾角為30°、45°、60°時救生艇落入規則波的過程進行分析;利用Kane方程為吊艇臂吊放救生艇運動建立模型,并改進文獻[16]中的運動模型。
1 救生艇自由降放
當釋放時,救生艇借助自身重力沿著滑道以背離母船方向向下滑行;離開滑道后,救生艇做自由落體運動。由于救生艇具有一定初始速度,使救生艇逐漸遠離母船,最終拋落入水。救生艇從脫鉤到入水整個過程不超過3 s。
1.1 過程分析
救生艇自由降放過程如圖 1。整個過程分為4個階段:下滑、旋轉、自由下落、入水。由位置1到位置2,艇在滑道上滑行;由位置2到位置3,艇作旋轉運動;由位置3到位置4,艇自由降落;由位置4到位置5,艇入水;最終艇浮出水面。

圖1 救生艇自由降落過程Fig. 1 The free-fall process of lifeboat
1.2 運動分析及建模
由于整個降放過程時間較短,故此段時間內救生艇滑道可視為靜止不動,救生艇所受空氣阻力對救生艇運動影響較小,可忽略不計。
1.2.1 下 滑
下滑過程為從救生艇被釋放到其重心靠近滑道最低點,此時運動方程如式(1):
(1)

1.2.2 旋 轉
旋轉過程為救生艇下滑結束到不在接觸滑道的過程,救生艇受力與下滑過程中所受力相同。此時,救生艇所受重力與滑道作用于救生艇的力的作用線不在同一條直線上,使救生艇發生轉動,其運動方程如式(2):
(2)
1.2.3 自由下落
自由下落過程為從轉動結束到救生艇接觸水面的過程。此時救生艇只受重力作用,但仍保持轉動狀態直到接觸水面。其運動方程如式(3):

(3)
1.2.4 入 水
自由降落結束后,救生艇開始入水,此時艇首底部接觸水面。由于救生艇速度較大,艇首受到巨大撞擊,艇首所受水動力與艇重力使救生艇轉動角速度減小,反轉直至艇平吃水,入水時救生艇受力情況如圖2。該階段運動方程如式(4):
(4)
式中:F、M、G分別為救生艇所受的水動力、水動力矩、重力;Fb、Mb分別為救生艇所受的浮力和由浮力產生的力矩;Fma、Fmn分別為作用于救生艇的軸向和法向力,這對力是當救生艇入水后,自身部分動量傳遞到周圍流體上而產生的作用力;Fda、Fdn分別為作用于救生艇的軸向和法向上的流體阻力;Mdn、Mmn為Fdn、Fmn產生的力矩。
作用于救生艇上的Fb、Fmn、Fdn是根據切片理論計算求得,將艇沿其軸向切分成等厚度橫截面,再對每個部分的受力進行計算,最終進行積分和修正。

圖2 救生艇入水時受力分析示意Fig. 2 Force diagram of lifeboat entering water
1.3 力和力矩的計算
分別對艇入水時所受的流體力及力矩Fda、Fdn、Fma、Fmn、Fb、Fmn、Mdn、Mmn、Mb進行計算[8]。
1.3.1Fb和Mb計算
救生艇浮力Fb與入水體積成正比,將每個部分浸入的橫截面積Ai(ξ)沿艇長積分求得入水體積,如式(5):
(5)
式中:ρ為海水密度;ξ為每個部分到艇重心距離。
1.3.2Fd和Md計算
艇運動坐標系下的流體阻力Fda、Fdn和力矩Mdn計算如式(6):
(6)
式中:2C為每個橫截面瞬時沉浸寬度;Acm為船中的橫截面積;Cda、Cdn分別為軸向和法向阻力系數;Vax、Vnr分別為艇沿軸向和法向速度。
Vax、Vnr由式(7)得出:
(7)
式中:γ(t)為波面高度。
1.3.3Fmn和Mmn計算
Fmn可根據文獻[3]計算得出,當物體進入水中時,其最初動量的一部分會傳遞給周圍水中。因此,作用于艇的力Fmn可通過自身動量變化率來計算。
假設動量轉化過程不可逆,則作用任意位置ξ厚度dξ橫截面的力如式(8):
(8)
式中:dm/dt為此部分附加質量m(ξ,h)對時間的導數;h為此部分淹深。
因為僅是計算救生艇入水,當Vnr>0時,dh/dt有意義;所以dh/dt=max(dh/dt, 0)。因此整個艇所受的力和力矩Fmn、Mmn為如式(9)、(10):
(9)
(10)
考慮救生艇軸向速度及救生艇底面與軸向的夾角α對Fmn、Mmn影響,對其進行修正,如式(11):
(11)
式(8)中m(ξ,h)為h(ξ)的函數,其關系如圖3。故圖2中h(ξ)可表示如式(12)、(13):
(12)
(13)
式中:C(ξ,h)為橫截面入水半寬值。

圖3 救生艇橫截面Fig. 3 Lifeboat cross-section
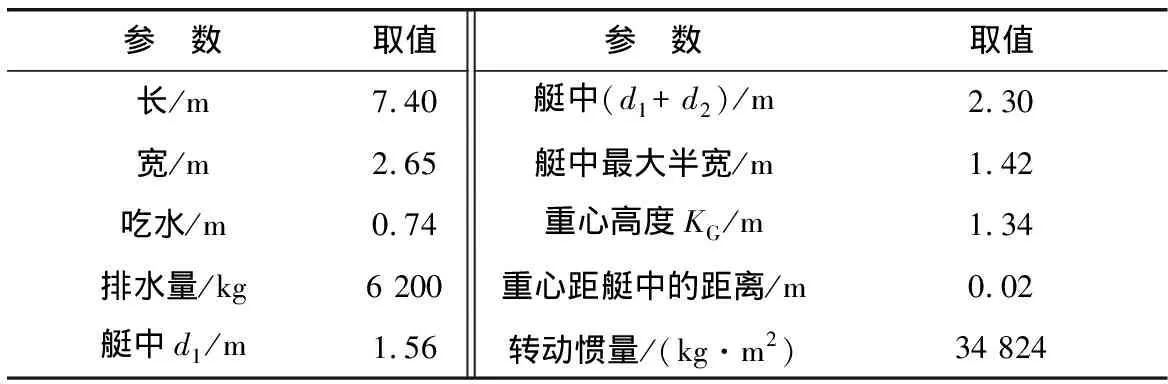
不同橫截面形狀不同,每個橫截面半寬值根據已有的數據插值計算得出,當d1 1.3.4Fma計算 對Fma的計算采用近似計算方法,通過計算艇首與艇重心處的平均加速度求得,如式(14): dl/dt=max(dl/dt, 0) (14) 式中:Lf為艇首與艇重心處的距離;m(l)為軸向附加質量;l為艇軸向入水長度。 則l和m(l)的計算如式(15)、(16): l=(γ-z)/sinθ+Lf (15) (16) max為艇完全進入水中時艇軸向的附加質量,如式(17): max=kπρL(d1+d2)2/6 (17) 通過上述方法對Fma及m(l)進行計算。其中:k為系數,大小取決于L/(d1+d2)。 將上面計算求得的力全部帶入式(4)中,即可計算出救生艇入水時在固定坐標系下的運動狀態,進而求得救生艇位置及軸向與水平角度。 救生艇入水運動狀態受很多種因素影響,如:滑道傾角、艇的質量分布、滑道長度、滑道距水面高度等。筆者基于救生艇實際尺寸,分析了不同滑道傾角對艇落入規則波的影響,救生艇基本資料如表1。 表1 救生艇基本信息Table 1 Basic information of boat 圖4為當其他條件不變,滑道傾角為30°、45°、60°時,救生艇落入波幅為0.5 m的規則波,其重心軌跡及艇首向變化。圖5為救生艇自由降落仿真效果。 圖4 重心軌跡及艇首向變化Fig. 4 Trajectory of gravity center and bow change 圖5 救生艇自由降落仿真效果Fig. 5 Simulation of lifeboat free-fall 救生艇在規則波作用下入水的仿真結果與文獻[8]結果非常相近,其運動趨勢一致。滑道傾角為30°時,艇入水點與滑道下端點水平距離距約為7.5 m;當滑道傾角為60°時,艇入水后會發生反向位移;當滑道傾角為45°時,艇入水后位移隨著艇進入波峰、波谷情況不同而改變,艇可能會發生反向位移情況。 救生艇吊艇臂是釋放和回收艇的主要設備。吊艇臂為門字形框架式起重臂,它與框架底座可轉動滾軸鉸接,使吊臂可上下起伏,借助吊臂起伏將救生艇收進和降放出吊艇架。吊艇臂起伏動力通過液壓動力系統提供。 由于吊艇臂與底座采用鉸鏈連接,此類約束為理想約束,故筆者利用Kane方法分析求解吊艇運動。 圖6為吊臂受力分析示意。圖6中:oxyz為固定坐標系;o1x1y1z1為局部坐標系,局部坐標系與吊艇臂固連;i、j、k為固定坐標系坐標軸的單位矢量;i1、j1、k1為局部坐標系坐標軸單位矢量。吊艇臂與水平線夾角為θ,吊艇臂逆時針轉動時,θ為正。不考慮理想約束,吊艇臂運動時,受驅動力矩為M,自身重力為G,吊艇索對其作用力為F,吊臂轉動慣量為Ic。各處摩擦、空氣阻尼忽略不計,吊艇鉤、繩索質量忽略不計。 圖6 吊臂受力分析示意Fig. 6 Force diagram of davit arm 作用于系統的主動力有吊艇臂重力(G=-m1gj),艇重力(G1=-m2gj),驅動力矩(T=Mk)。則系統廣義主動力如式(18): F(1)=(-m1gj)·L1j1+(-m2gj)·L2j1+Mk·k (18) 系統慣性力為-m1aC,-m2aD及對質心主矩T*=-ICε。則廣義慣性力如式(19): (19) 將廣義主動力和廣義慣性力帶入Kane方程,即可得系統動力學方程,如式(20)、(21): F*(1)+F(1)=0 (20) (21) 矢量點乘運算如式(22): (22) 式中:β為兩矢量間夾角。 在實際吊放救生艇過程中,吊艇臂轉動速度不大,且趨于平穩,救生艇運動也趨于平穩,故筆者忽略了救生艇在空中的晃動,救生艇運動保持在艇中縱刨面內,不發生扭轉。 各變量值分別為:θ=40°,L2=9.4 m,L1=5 m,m1=1 225 kg,m2=6 200 kg,Ic=1 200 kg·m2。 當液壓系統為吊艇臂提供驅動力矩時,即可求得吊艇臂轉動角速度和角加速度,進而求得吊艇臂的θ值。 圖7為在不同驅動力矩下,吊艇臂轉動的角度與時間的關系。吊艇臂旋轉角度與驅動力矩對應關系如圖8。 圖7 在不同驅動力矩下,吊艇臂轉動的角度與時間關系Fig. 7 Relationship between the angle and time of hoisting arm underdifferent driving moment 圖8 吊艇臂轉動的角速度一定時,吊艇臂轉動的角度與力矩關系Fig. 8 Relationship between the angle and the moment at the sameangular velocityof the crane arm rotation 由圖7可看出:若使用吊艇臂吊放救生艇時,至少需要驅動力矩約635 000 N·m才能啟動。由圖8可看出:隨著θ變大,所需驅動力矩變小。故在實際操作中,若保持吊艇臂平穩轉動,則需要不斷地調整驅動力矩。吊艇臂平穩轉動所需力矩比啟動力矩小很多。圖9則為系統仿真效果。 圖9 救生艇吊放仿真效果Fig. 9 Simulation of hoisting lifeboat 筆者為虛擬救生系統中自由降落式救生艇釋放過程的運動建立了數學模型,考慮到波面對艇入水時的影響,所建立模型能計算出艇在不同時刻的運動狀態;并應用Kane方程對艇吊放過程建立了模型,該模型簡單易算,滿足系統需要。由此得出以下結論: 1)當滑道傾角為30°時,艇入水點與滑道下端點的水平距離距約為7.5 m;當滑道傾角45°時,艇入水后可能會發生反向位移;滑道傾角60°時,艇入水后一定會發生反向位移; 2)在釋放救生艇時,一定要留出充分水域;當天氣惡劣時,要充分考慮救生艇會反向位移撞擊大船的情況; 3)吊艇臂吊放救生艇時,需要足夠大驅動力矩才能轉動;此力矩比吊艇臂平穩轉動所需力矩大很多;若保持吊艇臂平穩轉動,需要不斷調整驅動力矩; 4)在以后研究中,筆者應進一步完善救生艇運動模型:① 考慮復雜波面對艇入水影響;② 將二維運動模型提升至三維;③ 考慮艇與大船相互間的效應和耦合運動。1.4 結果與分析



2 救生艇吊放
2.1 坐標系建立及受力分析

2.2 偏速率、偏角速度
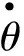
2.3 廣義主動力、廣義慣性力
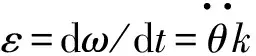
2.4 動力學方程
2.5 結果分析



3 總結與展望

