超寬混凝土主梁斜拉橋收縮徐變效應分析

黃 新，賈 烊，李建慧，王 濤

(1. 南京林業大學 土木工程學院，江蘇 南京 210037；2.南京市政設計研究院有限責任公司，江蘇 南京 210008)

作為混凝土的固有時變特性，收縮徐變能夠在較長時間內引起混凝土變形.收縮徐變變形受到約束后會在混凝土構件內部產生附加應力[1].為了計算混凝土構件的收縮徐變效應，學者們在試驗的基礎上提出了一系列收縮徐變預測模型，其中CEB-FIP1990預測模型為我國公路橋梁設計規范所采納[2-3].計算理論方面，將按齡期調整的有效模量法(AEMM)結合有限單元步進法(FEM)，便于編制程序計算混凝土構件的收縮徐變效應[4-5].

斜拉橋屬高次超靜定結構，收縮徐變作用下斜拉橋結構的力學響應受到了國內外研究者的廣泛關注.根據周履[6]的介紹，英國迪河斜拉橋的工程師通過修正預測模型預估收縮徐變變形量，在主梁線形控制方面取得了良好的效果.陳太聰等[7]基于等效增量荷載原理編制了混凝土主梁斜拉橋節段施工收縮徐變計算程序.蘇成等[8]基于響應面-蒙特卡羅法對一座獨塔雙索面斜拉橋進行了收縮徐變隨機分析.而與普通寬度主梁斜拉橋相比，超寬主梁斜拉橋混凝土用量大且一般均設置有多道橫梁.超寬主梁在縱橫向預應力和拉索力的共同作用下內力分布狀況復雜，而混凝土徐變與構件應力狀態密切相關，因此有必要研究超寬混凝土主梁斜拉橋的收縮徐變效應.斜拉橋收縮徐變受材料組成、施工工藝和環境條件等因素耦合作用[9]，現有文獻對超寬混凝土主梁斜拉橋的收縮徐變參數敏感性研究較少.本文依托實際工程，建立超寬混凝土主梁斜拉橋全橋梁格模型，基于AEMM-FEM法和灰色關聯度方法對該橋進行收縮徐變參數敏感性分析.

1 工程概況

某獨塔雙索面斜拉橋跨度為185 m(100 m+85 m)，塔柱為橢圓型鋼箱混凝土結構，為墩塔梁固結體系，全橋布置情況如圖1所示.主梁和橋塔均采用C50混凝土，斜拉索與預應力鋼束材料分別為鋼絲和鋼絞線.超寬主梁采用雙邊箱形式，邊箱結構為預應力混凝土單箱雙室，橋面寬為37 m，主梁橫斷面如圖2所示.

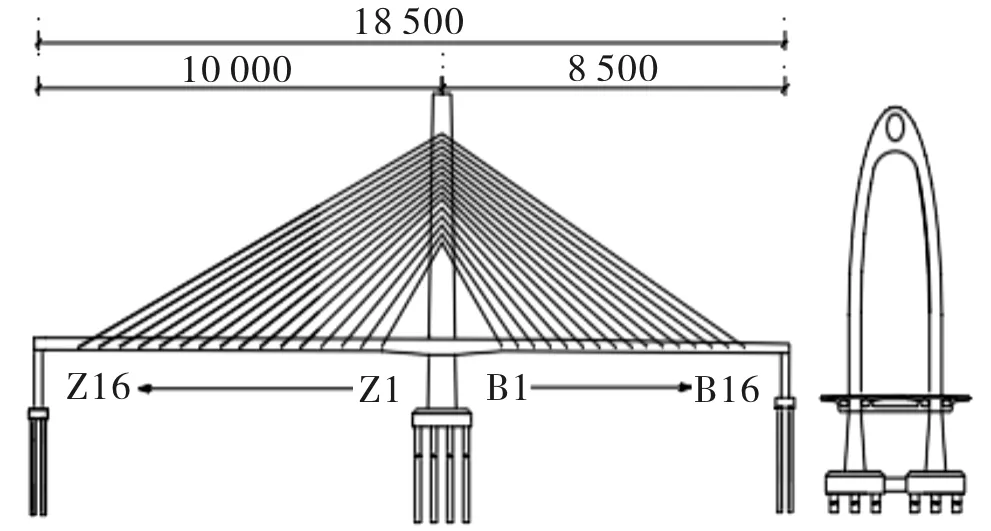
圖1 全橋布置圖(單位：cm)Fig. 1 Layout of the bridge (Unit: cm)

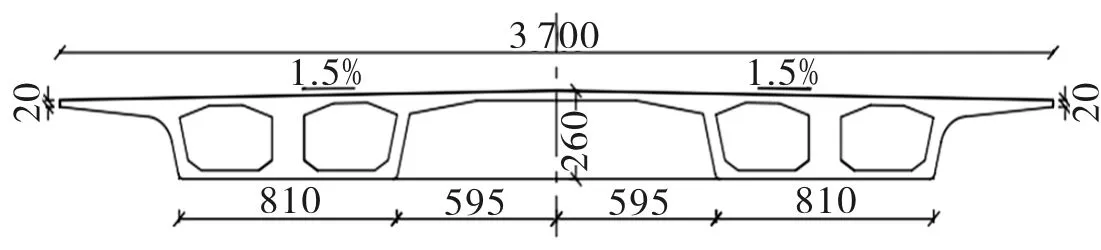
圖2 主梁橫斷面(單位：cm)Fig.2 Cross section ofthe girder (Unit: cm)

2 有限元建模

2.1 全橋空間梁格模型

利用Midas/Civil有限元軟件建立全橋空間梁格模型，由于超寬主梁具有腹板距離大、翼緣板寬且箱壁薄的特點，為了準確反映結構的受力特性，采用剪力-柔性梁格法[10]模擬超寬混凝土主梁，將主梁劃分為6根縱梁.橋塔和斜拉索分別采用梁單元和只受拉桁架單元模擬，在模型中考慮的荷載作用主要包括自重、拉索力、預應力、二期恒載和城-A級汽車荷載.根據設計資料劃分施工階段：主塔和邊跨主梁施工時間共計150 d；主跨主梁各節段懸臂澆筑施工時間為15 d；在主跨主梁各節段的施工過程中，對稱張拉兩側斜拉索的時長為2 d；施工橋面鋪裝和附屬設施、拆除支架的持續時間共計35 d.全橋有限元模型見圖3，在表1中列出了模型的邊界條件，主要構件的材料參數見表2.

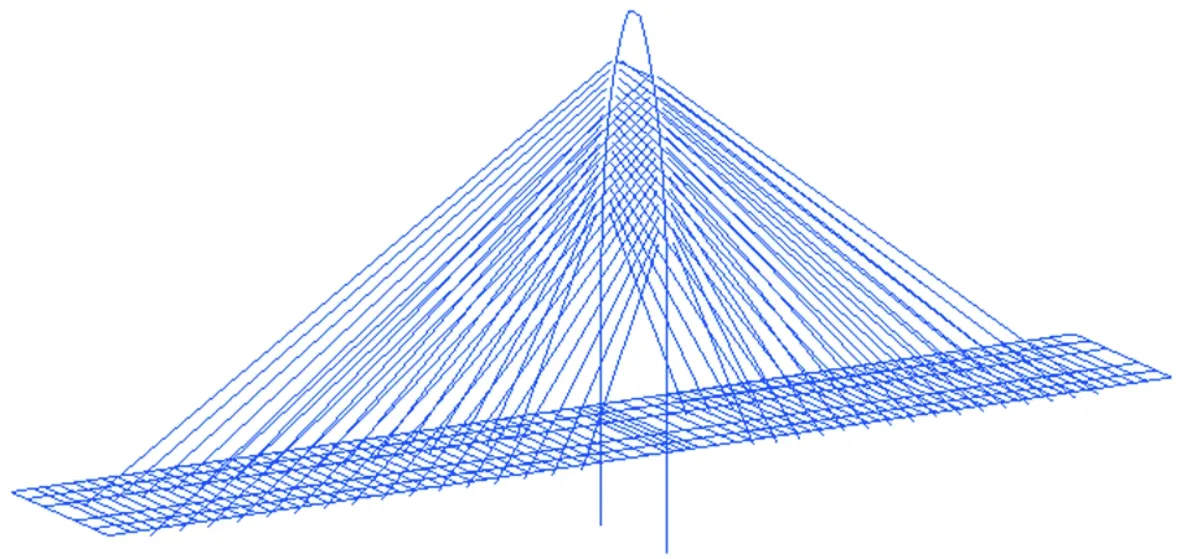
圖3 全橋空間梁格模型Fig.3 Spatial grillage model of the bridge

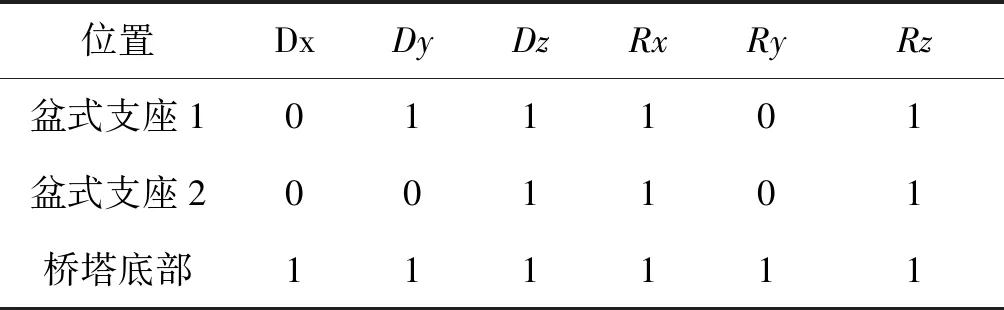
位置DxDyDzRxRyRz盆式支座1011101盆式支座2001101橋塔底部111111

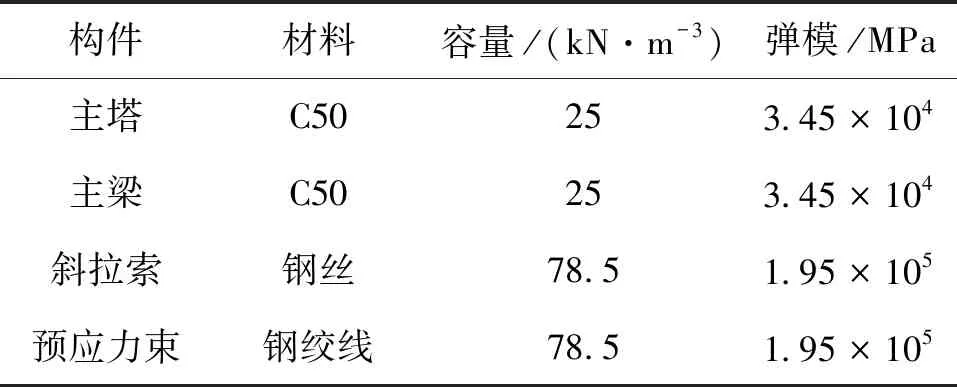
表2 主要材料參數

2.2 模型驗證

為了驗證有限元模型的準確性，進行全橋動力特性試驗.沿縱橋向選取主梁振動測試截面，J1～J3截面位置為主跨主梁三分點， J4截面位于邊跨主梁跨中，圖4為現場試驗情況.在環境激振作用下得到前4階結構固有振動頻率實測值和模型理論值，分析結果如表3所示.

圖4 現場試驗圖Fig.4 Photos of field test

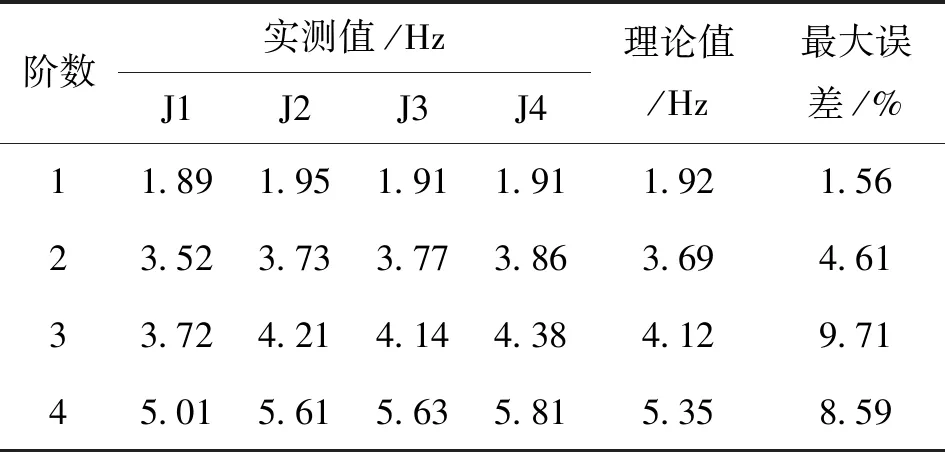
階數實測值/HzJ1J2J3J4理論值/Hz最大誤差/%11.891.951.911.911.921.5623.523.733.773.863.694.6133.724.214.144.384.129.7145.015.615.635.815.358.59

由表3可知，在相應振型階次下主梁固有振動頻率實測值與理論值較為接近，最大誤差值均在10%以內，說明空間梁格模型結構剛度與實際情況基本吻合，此模型可以作為收縮徐變參數分析的基準模型.

3 計算理論

3.1 AEMM-FEM收縮徐變分析方法

試驗結果表明，當混凝土應力低于其極限強度的40%～50%時，終極徐變變形與初始彈性變形近似呈線性關系，分批加載應力后產生的應變可以疊加[11].Bazant教授據此推出混凝土收縮徐變總應變增量表達式：

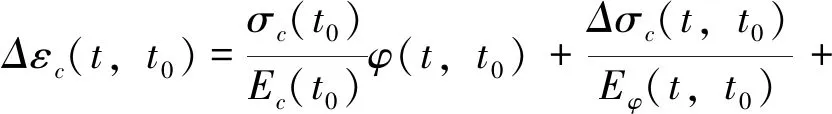
(1)

式中，Eφ(t,t0)為按齡期調整后的混凝土彈性模量；φ(t,t0)為徐變系數；εcs(t,t0)為收縮應變.

將施工過程細化為若干個計算時段，則在單個時段內收縮徐變產生的應力增量與應變增量為線性關系，可以利用有限單元法和逐步遞推法迭代計算混凝土收縮徐變引起的內力和位移.

3.2 灰色關聯度分析方法

灰色關聯度分析方法通過計算關聯度序列，得到元素對于系統的影響敏感性差異[12]，步驟如下：

(1)原始數據矩陣的無量綱化處理：選擇m個敏感性參數組成自變量比較矩陣，每種參數包括n個取值，相應的系統影響值組成因變量參考矩陣.以自變量矩陣元素為例，對原始數據矩陣元素作均值無量綱化處理.

(2)

(2)確定灰色關聯差異信息矩陣：對自變量矩陣與因變量矩陣各元素逐一進行差值絕對化計算建立差異信息矩陣Δ，提取Δ中的最大值M與最小值m，計算關聯系數.

(3)

(4)

為了強化關聯系數之間的差異性，分辨系數δ取0.5.

(3)計算灰色關聯度序列：對同一自變量的關聯系數取平均值作為該自變量與系統因變量之間的關聯度.

(5)

將關聯度按數值大小進行排序，關聯度越大說明該因素對系統影響的敏感性越大.排序結果與采取的數據處理方法無關，分析結果具有可靠性.

4 收縮徐變效應分析

4.1 混凝土收縮徐變參數設置

采用CEB-FIP1990預測模型反映混凝土材料的收縮徐變規律，選擇主梁加載齡期X1、混凝土收縮齡期X2、環境相對濕度X3、主梁混凝土強度X4作為參數分析的變量.將基準模型的成橋運營時間統一設置為100 d，橋塔加載齡期為7 d，基準模型的X1、X2、X3、X4分別取10 d、3 d、70%和50 MPa.

4.2 超寬主梁負彎矩區影響分析

提高混凝土收縮徐變參數值，超寬主梁最大負彎矩截面上、下緣壓應力變化如圖5所示，超寬主梁最大負彎矩變化分別如圖6所示，負值代表截面壓應力或負彎矩減小.

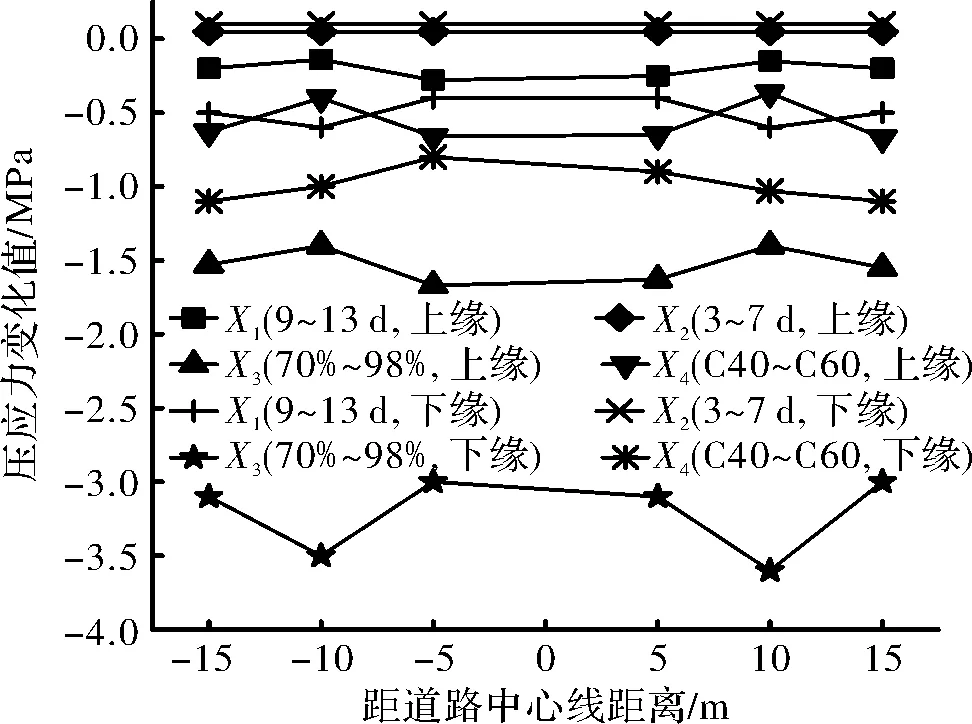
圖5 壓應力變化Fig.5 Change of compressive stress

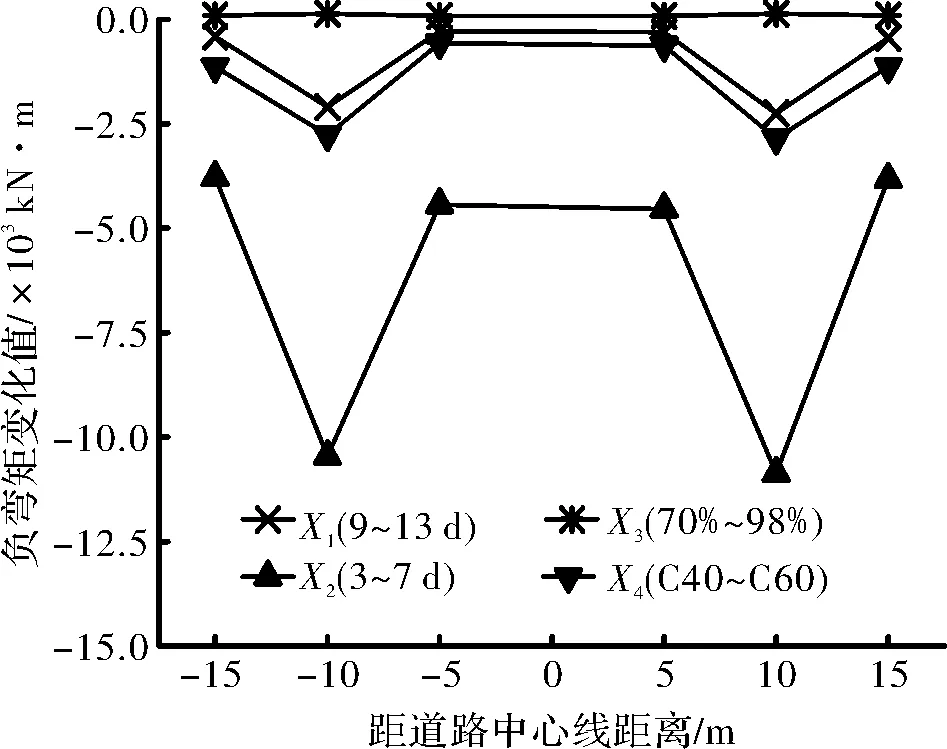
圖6 最大負彎矩變化Fig.6 Change of maximum negative moment

由圖5和圖6可知，在超寬主梁最大負彎矩位置中，截面上、下緣壓應力和負彎矩均隨著主梁加載齡期、抗壓強度和環境相對濕度的增加而減少.其中，環境相對濕度升高引起的下緣壓應力和負彎矩變化量最大，減少率分別達14.57%和8.99%.截面上緣壓應力變化量小于下緣，這是由于負彎矩區主梁頂板厚度小于底板，而頂板配筋率大于底板，在鋼筋的抑制作用下，收縮徐變對主梁截面上緣應力的影響相對較小.上、下緣應力和彎矩變化值在橫截面上分布不均勻，整體呈波浪形曲線，可知超寬主梁收縮徐變的空間效應顯著.由于斜拉索錨固在主梁底板，斜拉索預埋管處于中腹板范圍內，索力荷載對中腹板應力狀態的影響較大，進而影響中腹板的徐變效果.同時，超寬主梁中腹板厚度大于斜腹板，收縮徐變對中腹板的影響更大.因此，超寬主梁中腹板對收縮徐變參數更為敏感.

4.3 索力影響分析

超寬混凝土主梁斜拉橋斜拉索具有數量多、空間分布廣、索力均衡性要求高的特點，索力分布狀態影響結構整體受力性能.篇幅所限，僅列出收縮徐變各參數影響下單側索力的變化情況，數據如圖7所示，負值代表索力減小.

從圖7可以看出，提高主梁加載齡期、主梁抗壓強度和環境相對濕度對索力的影響趨勢一致：跨中區域斜拉索發生應力松弛現象，梁端附近斜拉索的索力負擔加重.其中，主梁抗壓強度變化引起的索力下降幅度最大，跨中區域索力松弛率達1.44%.環境相對濕度從70%提高至98%，Z16號索的內力增長率達4.42%.這是由于在混凝土收縮徐變的作用下，橋塔和主梁均會產生結構變形，拉索錨固點偏離初始幾何位置，導致索力不均衡程度加劇.

4.4 收縮徐變參數敏感性分析

選擇主梁最大撓度Y1、塔頂縱向偏移距離Y2作為結構變形程度的評價指標.分析時改變基準模型的某一參數，控制其他參數不變，基準模型的參數取值情況如前所述.不同收縮徐變參數條件下，超寬混凝土主梁斜拉橋結構線形的響應值見表4.

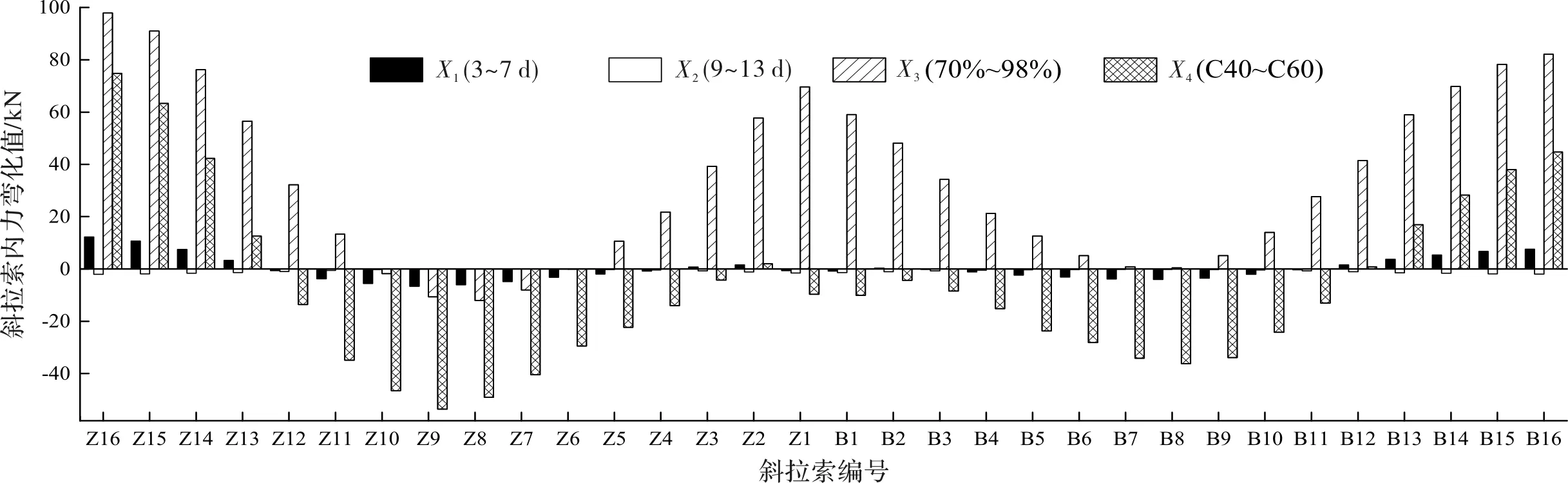
圖7 斜拉索內力變化Fig.7 Change of internal force of stay cables

收縮徐變參數X主梁撓度最大值Y1/mm塔頂縱偏值Y2/10-2mmX1/dX2/dX3/%X4/MPaY1Y2Y3Y4Y1Y2Y3Y4937040-68.15-67.65-67.65-72.92-366.48-368.64-368.64-334.341047745-67.65-67.70-64.41-70.09-368.64-368.78-365.80-352.441158450-67.21-67.74-61.01-67.65-370.52-368.93-362.20-368.641269155-66.81-67.80-57.76-65.52-372.15-369.10-357.91-383.331379860-66.45-67.86-56.36-63.84-373.62-369.29-353.53-391.22

注：負值代表坐標軸負方向

由表4的數據可知，環境相對濕度、主梁加載齡期增加，超寬主梁撓度均呈減小趨勢.這是由于混凝土構件在濕度較大的環境下材料吸附水蒸發量減少，使得混凝土的水泥水化反應更加充分，收縮徐變效應得到減輕.加載前，混凝土在自重作用下發生初始收縮徐變變形，而收縮徐變變形總量趨于收斂，提高主梁加載齡期將會壓縮構件使用期間的收縮徐變發展空間.加載齡期增加后，混凝土在使用階段彈性模量的起點較高，在一定程度上限制了構件徐變變形能力.橋塔變形方面，僅環境相對濕度的升高會緩解塔頂縱向偏移程度.其中，主梁抗壓強度變化引起的塔頂位移最大，抗壓強度從C40提高至C60，塔頂偏移變化率達17.01%.

對表2中的數據進行初始列陣，按照灰色關聯度方法進行數值計算.收縮徐變參數與超寬主梁撓度之間的關聯度矩陣為

收縮徐變參數與塔頂縱偏值之間的關聯度矩陣為

按數值大小對灰色關聯度進行排序，結果為

由灰色關聯度序列可知，主梁加載齡期是影響超寬主梁線形的最敏感因素，其次是主梁抗壓強度、環境相對濕度、收縮齡期的影響.塔頂位移受主梁抗壓強度的影響最為嚴重，主梁加載齡期、環境相對濕度和收縮齡期的影響依次遞減.

5 結論

通過對超寬混凝土主梁斜拉橋進行收縮徐變參數敏感性分析，得出如下結論：

(1)主梁加載齡期、抗壓強度和環境相對濕度變化時，超寬主梁負彎矩區截面應力與彎矩變化值沿橫向分布不均，索力不均衡現象凸顯.為保障結構的使用安全，設計時應對收縮徐變相關材料參數合理取值，同時考慮環境濕度季節性變化對結構受力性能的影響.

(2)根據灰色關聯度分析結果，主梁加載齡期是影響超寬主梁線形的最敏感因素.超寬主梁撓度隨著主梁加載齡期的增大而減小，施工時應為主梁早期收縮徐變留足時間，以減輕收縮徐變的不利影響.