太沙基地基極限承載力的三剪應力統一強度理論解

高江平，胡海波，孫世界，王澤普

(長安大學 特殊地區公路工程教育部重點實驗室，陜西 西安 710064)

工程領域對地基承載力的探究是巖土工程學科一個重要的問題，因為地基穩定性的影響因素很多，對工程的各項性能評估具有重要的意義.

強度準則揭示了物體受力狀態下產生塑性形變和損壞的現象.目前，巖土材料研究中多采用Terzaghi準則和Mises準則解決實際問題[1].但是在實際運用中發現，其分別存在各自的局限性.前者在實際運用中忽視了中主應力的作用.而后一準則比較復雜，不存在相關性，實際運用中通常只能采用數值法進行求解.

1943年，太沙基首次依據Mohr—Coulomb理論提出了地基承載力公式[1]，沿用至今.但是，在運用中發現，太沙基地基最大承載力公式未考慮中主應力，因而無法徹底揭示地基的真實破壞狀況.

本文根據三剪統一強度理論，可求得基于此理論下的太沙基地基極限承載力值，并探究權系數b、c對其的影響.

1 三剪應力統一強度理論[3]

該理論認為：菱形十二面單元體上的三個主剪應力(τ13、τ12、τ23)與三個正應力(σ13、σ12、σ23)構成的函數關系式達到某一極限值時，材料產生損壞.其數學公式為

F=τ13+bτ12+cτ23+β(σ13+
bσ12+cσ23)=f

(1)

也可將式(1)表示成以下形式：

F=τ13+βσ13+b(τ12+βσ12)+
c(τ23+βσ23)3=f

(2)

式中：β為在正應力作用下材料損壞的強度影響參數，b為在τ12和σ12作用下材料損壞的影響系數，c為在τ23和σ23作用下材料損壞的影響系數，b與c均在0～1范圍內取值，f為材料強度參數.

建立了此理論下的內摩擦角φs、粘聚力cs公式[3]：

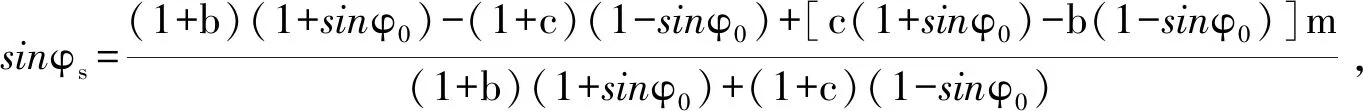
(3)

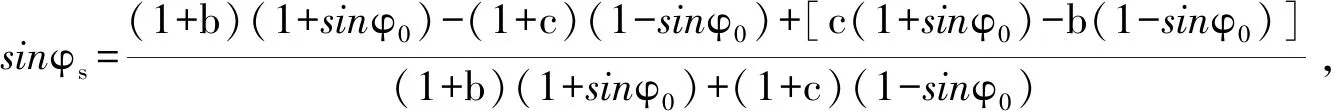
(4)

(5)

式中：φ0和c0為Mohr-Coulomb理論下的內摩擦角和黏聚力，σ2=m(σ1+σ3)/2，且m在0到1之間取值，當材料處于彈性階段時，m可取值為2v，其中v表示材料泊松比，當材料處于屈服變形狀態時，m→1.

2 太沙基地基承載力的三剪統一強度理論解

2.1 基本假設

(1)假設地基作用面不光滑，摩擦力很大.整個地基產生貫穿至基底的剪切破壞，產生持續的滑動，基底下局部土體與基礎同時移動，從而該土體一直保持彈性狀況，區域Ⅰ為彈性楔體.該局部土體與滑動土體分界線用ab表示，并假設分界線ab與基礎底平面的夾角用ψ表示，如圖1所示.

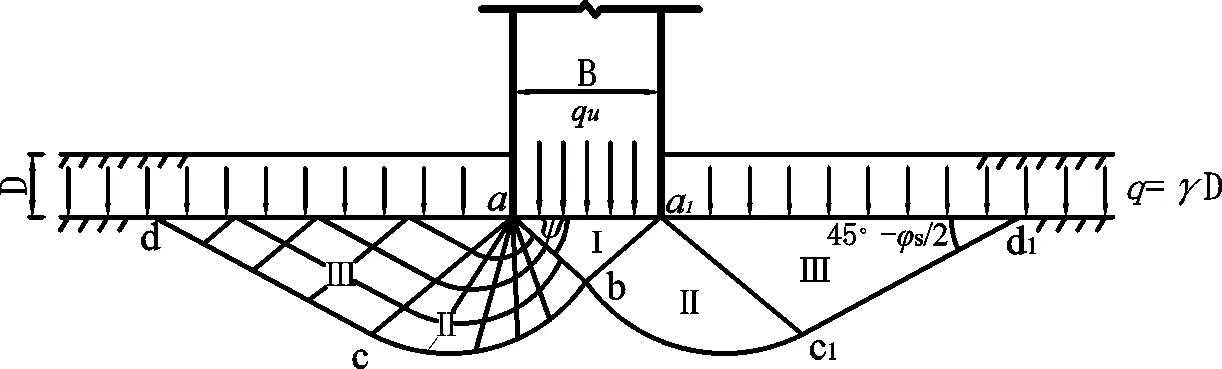
圖1 基底粗糙情況下的滑動面形狀Fig.1 Sliding surface shape of rough base

(2)徑向剪切區域Ⅱ與朗金被動區域Ⅲ形成滑動區域，且所有滑動區的土體(區域Ⅰ除外)均保持在塑性平衡狀況，區域Ⅱ的界線bc用以下公式表達：

(6)

式中：r0為初始位置矢量，θ為任意位置矢量r與初始位置矢量r0的夾角.

區域Ⅲ的界線cd是一條直線，與水平面的夾角為45°-φs/2.

(3)考慮在基礎兩側地基上施加均布超載q=γD，來抵消土體抗剪強度的影響.

2.2 地基極限承載力公式

由2.1中的假設條件，通過圖2所示的區域Ⅰ三角形aba1的平衡關系，推導出整個剪切破壞情況下的極限荷載表達式：

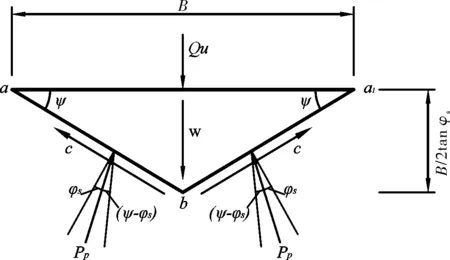
圖2 區域Ⅰ彈性楔體受力示意圖Fig.2 Stress diagram of elastic wedge in Region I

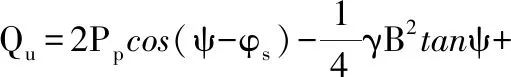
(7)

式中：γ為基礎以下土體的重度，B為基礎底部寬度，c0和φ0為基礎以下土體的抗剪強度參數；作用力Pp為一合力，由基礎以下土體的粘聚力c0、基礎以下土體的重度γ產生的被動土壓力和超載q組成，其作用面為區域Ⅰ的分界面ab，即

PP=PPc+PPq+PPγ

(8)

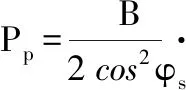
(9)

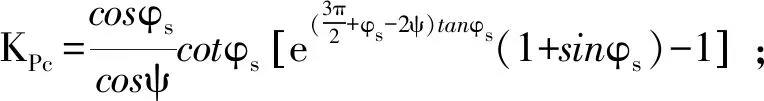
Kpγ為基礎以下土體的重度γ所產生的被動土壓力的作用系數，確定Kpγ需要采用試算方法.

聯立公式(7)與公式(9)推導得出：

(10)

其中：

(11)

式中，Nc、Nq、Nγ為無法量化的承載力系數指標，只和φ0有關.

式(10)是以基底粗糙為條件推導出的，并且圖2中ψ是未知的.故作如下假定：

(1)假定基礎完全粗糙.此時作出如下假定：認為ψ=φs，基礎底部滑動面形狀如圖3.

圖3 基底完全粗糙情況下的滑動面形狀Fig.3 Sliding surface shape of completely rough base

則可將式(11)的形式表示成如下情形；

(12)

從式(12)可知：系數Nc、Nq、Nγ均受到基礎以下土顆粒間摩擦角φ0的影響，一般需要通過試算確定被動土壓力系數Kpγ.

工程運用上為了方便，對于系數Nγ，往往聯合太沙基經驗公式，采用如下式確定：

Nγ=1.8(Nq-1)tanφs

(13)

(2)假定基底完全光滑.則區域Ⅰ的土體狀態轉變成朗金主動狀態，從而使得區域Ⅰ與區域Ⅱ和區域Ⅲ共同構成一個完整的滑動區，這時區域Ⅰ的界線ab與水平面的夾角ψ(如圖3～圖4所示)有如下表達式：

將ψ代入式(11)中，可分別得到此條件下的系數Nc、Nq、Nγ.

火箭測試廠房平開大門(下簡稱大門)能夠實現大門的水平方向移動,從而實現矩形門洞的閉合與打開,是各航天發射場廣泛使用的一種特種機械設備,它具有抗沖擊能力強、工作可靠性高、制造工藝相對簡單等優點.但是由于廠房需求不同,加之不同時期的設計能力、計算能力也千差萬別,造成發射場大門形式多樣,裝備化保養困難.隨著航天發射場的不斷發展,傳統意義上粗大笨重、操作復雜、維護困難的廠房大門已經無法適應發射場特種設備“三化”的要求,結合某發射場火箭廠房擴建工程新建大門,對發射場現有各種大門的功能和結構模式，進行統計分析和梳理分類,從大門系列化的角度,本著有限目標,重點突出的原則,研究大門的模塊化設計方法.

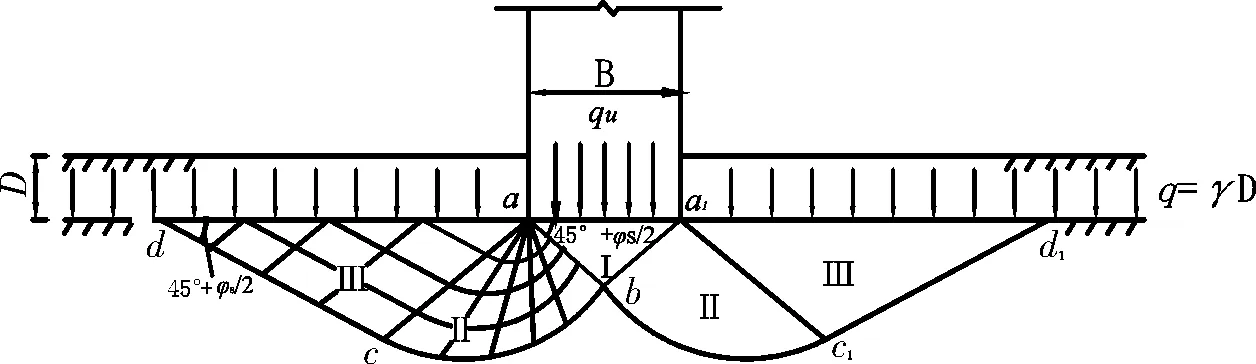
圖4 基底完全光滑情況下的滑動面形狀Fig.4 Sliding surface shape of completely smooth base

3 算例

現有某地基，土的重度γ=19.5 kN/m3，土體均勻，為粘性土.經固結不排水條件下快速剪切試驗，測得c0=20 kPa，φ0=22°.地基土上埋置一長條基礎，深度3 m，寬度4 m.

根據以上已知條件，分別基于四種不同的理論，求解地基極限承載力值，并進行比較分析.

3.1 經典太沙基公式解[1]

3.1.1 當基礎底部為完全粗糙狀態時，根據題設條件φ0=22°計算得出承載力系數Nc=20，Nq=10，Nγ=7.最后解得地基極限承載力qu=1 258.0 kPa.

3.1.2 當基礎底部為完全光滑狀態時，根據題設條件φ0=22°計算得出承載力系數Nc=16.88，Nq=7.82，Nγ=4.96.最后解得地基極限承載力qu=988.5 kPa.

3.2 雙剪強度理論解[6,8]

地基承載力達到其極限值，此時地基處于屈服破壞的臨界狀態，中間主應力參數m=1.

當基礎底部為完全粗糙狀態時，根據題設已知條件，計算得到承載力系數Nc=27.5，Nq=14.78，Nγ=12.3.從而最終解得極限承載力為qu=2 017.7 kPa.

3.3 雙剪統一強度理論解[5]

地基承載力達到其極限值，此時地基處于屈服破壞的臨界狀態，此時中間主應力參數m=1.

當基礎底部處于完全粗糙時，假設系數b(0≤b≤1)分別取0、0.2、0.4、0.6、0.8、1，解得極限承載力如下表1所示.

表1 完全粗糙基底條件下的地基極限承載力值

當基礎底部處于完全光滑狀態時，假設系數b(0≤b≤1)分別取0、0.2、0.4、0.6、0.8、1，解得極限承載力如下表2所示.

表2 完全光滑基底條件下的地基極限承載力值

3.4 三剪應力統一強度理論解

地基承載力達到其極限值，此時地基處于屈服破壞的臨界狀態，此時中間主應力參數m=1.利用上文中推導的公式分別計算.

(1)當基礎底部處于完全粗糙狀態時，系數b與c分別在0～1之間取值，從而解得相應的極限承載力值，如表3所示，并繪制了此條件下系數b、c與qu之間的關系圖，如圖5所示.

表3 完全粗糙基底條件下的地基承載力值

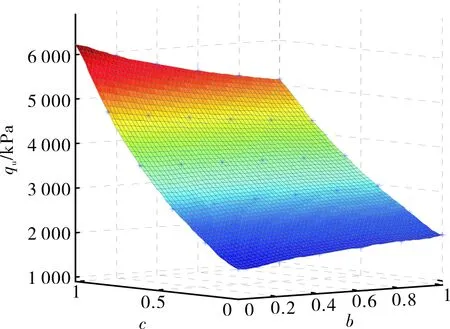
圖5 完全粗糙基底條件下系數b、c與qu之間的關系圖Fig.5 Correlation graphs between b, C and qu on completely rough base

從表3及圖5中可以看出地基極限承載力qu受到b、c取值的影響，b、c取值越大，則qu越大.由表3的計算結果與3.1.1的結果相比可知，本理論的承載力值均大于經典太沙基承載力值；與3.2.1的結果相比可知，當b=1，c在0～1之間取值時，本理論的承載力值均大于雙剪強度理論的承載力值；與3.3.1相比，當c=0，b在0～1之間取值時，式(1)蛻化成雙剪統一強度理論，本理論的承載力值即為雙剪統一強度理論的承載力值，當b=1，c在0～1之間取值時，則本理論的承載力值均大于雙剪統一強度理論的承載力值，由此表明：極限承載力在較大程度上也受到系數c的影響，且隨著c值的增加而增大.

(2)當基礎底部處于完全光滑狀態時，系數b與c分別在0～1之間取值，最終解得相應的極限承載力值，如表4所示，并繪制了此條件下系數b、c與qu之間的關系圖，如圖6所示.

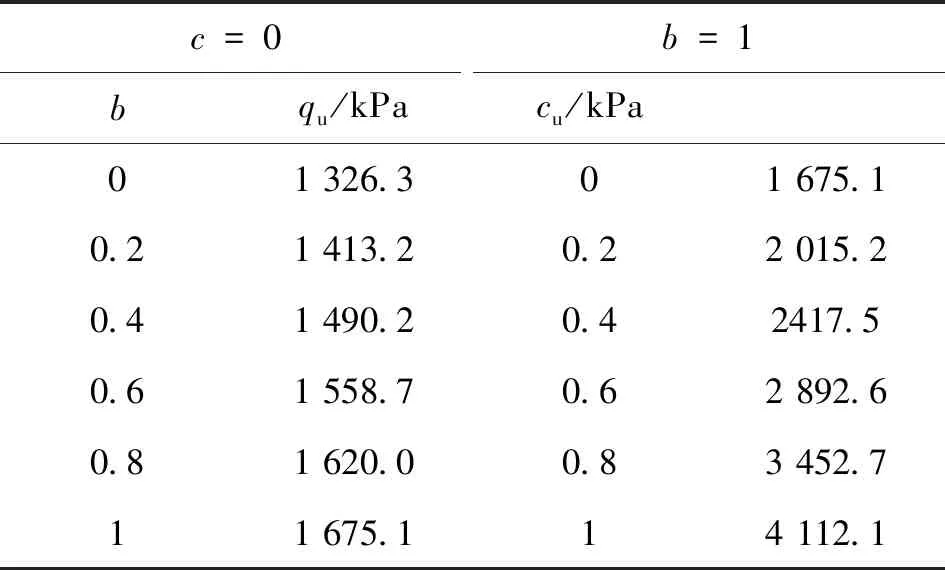
表4 完全光滑基底條件下的地基承載力值

圖6 完全光滑基底條件下系數b、c與qu之間的關系圖Fig.6 Correlation graphs between b, c andqu on completely smooth base

從表4及圖6中也可以看出地基極限承載力qu受到b、c取值的影響，b、c取值越大，則qu越大.由表4的計算結果與3.1.2的結果相比可知，本理論的承載力值均大于經典太沙基承載力值；與3.2.2的結果相比可知，當b=1，c在0～1之間取值時，本理論的承載力值均大于雙剪強度理論的承載力值；與3.3.2相比，當c=0，b在0～1之間取值時，式(1)蛻化成雙剪統一強度理論，本理論的承載力值即為雙剪統一強度理論的承載力值，當b=1，c在0～1之間取值時，則本理論的承載力值均大于雙剪統一強度理論的承載力值，由此表明：極限承載力在較大程度上也受到系數c的影響，且隨著c值的增加而增大.

4 結論

(1)本文推導出了太沙基地基極限承載力的三剪統一強度理論解，并可根據系數b、c的不同取值，將此理論解簡化為其他不同的理論解.若b和c值均為0，則簡化為Mohr—Coulomb理論解；若b不為0，而c值為0，則簡化為雙剪統一強度理論解.

(2)本文公式分別包含了以經典太沙基、雙剪強度理論及雙剪統一強度理論為依據的地基承載力公式，并與前三種理論解進行了對比分析表明：三剪統一強度理論解更加全面的考慮了材料中三個主剪應力的影響，將其潛能發揮的更大，既克服了傳統太沙基公式保守的缺點，又將雙剪統一強度理論中忽略的最小主剪應力考慮進來.

(3)隨著系數b、c值的增加，由本文推導的三剪應力地基承載力值也在提高.三剪統一強度理論解適用范圍很廣，適用于許多不同類型地基的承載力計算，通過合理地確定b、c值從而得到更為真實的結果.