含水量對珠三角軟土時效變形特性影響試驗分析與模型研究

童華煒, 方曉填， 劉柱輝，袁 杰

(1.廣州大學 土木工程學院，廣東 廣州 510006；2.中交(廣州)鐵道設計研究院有限公司，廣東 廣州 510290)

軟土是由固體土顆粒、孔隙水、孔隙氣和吸附在顆粒群表面的結合水膜及顆粒間膠體等物質組成的多相介質，廣泛分布于沿海、江河的中下游及湖泊的三角洲地區，其物理力學性質和工程特性較復雜且區域差異性明顯.土體時效變形特性是指土體在恒定荷載作用下產生的變形與時間的關系，包括加載前期的滲流固結變形和加載中后期的時效變形[1].土體的時效變形特性是影響地基長期強度和長期變形穩定性的關鍵因素，是學術界和工程界研究的重要課題之一[2].

珠江三角洲由于經歷復雜的海侵、海退與江水的共同作用，使得該地區軟土在層理特征和物理力學性質上與其它沉積相軟土層之間存在一些明顯差異特征，如土層的均勻性極差、平面分布不規則、與粉細砂層呈互層狀產出等，且因沉積時期，埋藏深度、夾層厚度及分布情況和內容物(部分軟土含有牡蠣、貝殼及腐殖質等)的不同，不同區域又表現有明顯的差別，這使得珠三角軟土具有承載力低、受荷后變形大、時間效應明顯、與建筑物共同作用能力強等特性.這對區域內的工業與民用建筑工程、道路橋梁工程、堤防工程、機場工程等都產生很大影響[3-4].

因此，對于深入研究軟土的物理力學性能和工程特性，有著積極而重大的經濟價值和社會作用.科學研究試驗和大量工程經驗表明，當土的應力和施加的荷載一定時，土的含水率變化會引起土的時效變形特性變化.軟土地區的建筑物建成后的變形一般歷時幾年甚至長達幾十年，可能會產生過大的變形，引起不均勻沉降.不論對短期還是長期活動都會產生較大的影響，這都必須引起人們的高度重視[5-7]但是由于地域的差異、沉積原因不同、氣候水文環境的差別，各地區的軟土時效變形特性不盡相同[1].

采用改進的直剪蠕變儀，在相同試驗條件下完成了5組不同含水量及不同應力水平試樣時效變形特性的測試；獲得了試樣含水量與時效變形特性的關系；研究了不同含水量、不同應力水平組合下的模型擬合.基于含水量變化，對珠三角軟土室內直剪試驗數據進行模型分析，并分析得出相關參量，通過相關系數對比分析各模型的擬合程度.

1 蘿崗軟土流變試驗

1.1 試樣制備與試驗方案

試驗采用廣州蘿崗軟黏土為代表性土樣，試驗儀器采用改進后的三聯裝直剪蠕變儀(見圖1).根據其界限含水量范圍共設計1組5個試樣進行直剪蠕變試驗，各試樣的含水量w依次為8.5%(0.27ωp)，16.4%(0.53ωp)，31.5%(ωp)，58.1%(ωL)，70.2%(1.22ωL)[8].各試樣編號、成分及主要物理參數見表 1，因試樣的抗剪強度會隨著含水量的提高而降低，適當減小了試樣ZJ4與ZJ5的水平剪應力增量，直接剪切蠕變試驗方案見表 2.試樣制備方法參考《土工試驗方法標準》(GB/T50123-1999).

圖1 改進后的直剪蠕變儀Fig.1 Improved direct shear creep apparatus

直剪蠕變穩定的標準為：當施加的剪應力水平較低時，試樣通常處于衰減蠕變階段，24 h內剪切位移小于0.005 mm時可視為蠕變達到穩定，此時可以施加下一級剪切荷載.當施加的剪應力較大，試驗可能出現等速蠕變階段時，待剪切變形速率趨于勻速后，再施加下一級荷載[9].

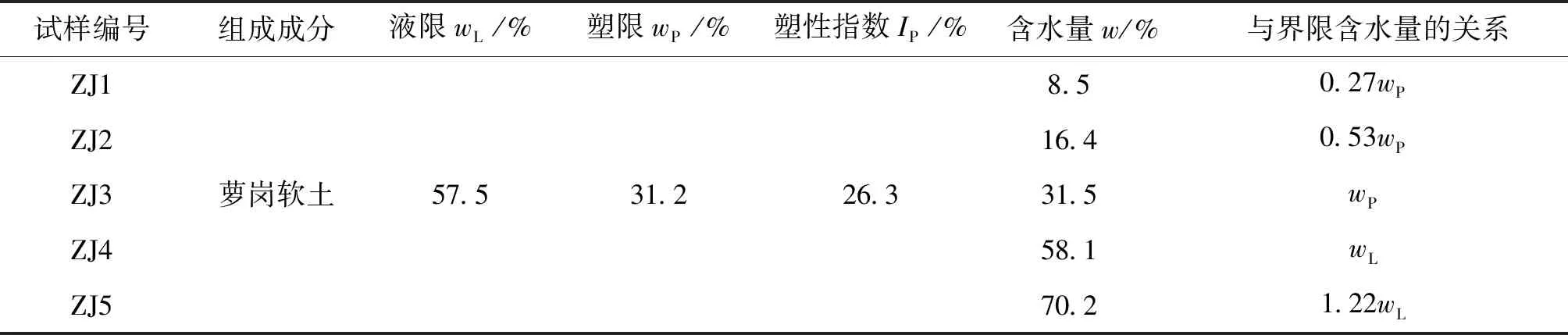
表1 土樣主要物理力學性

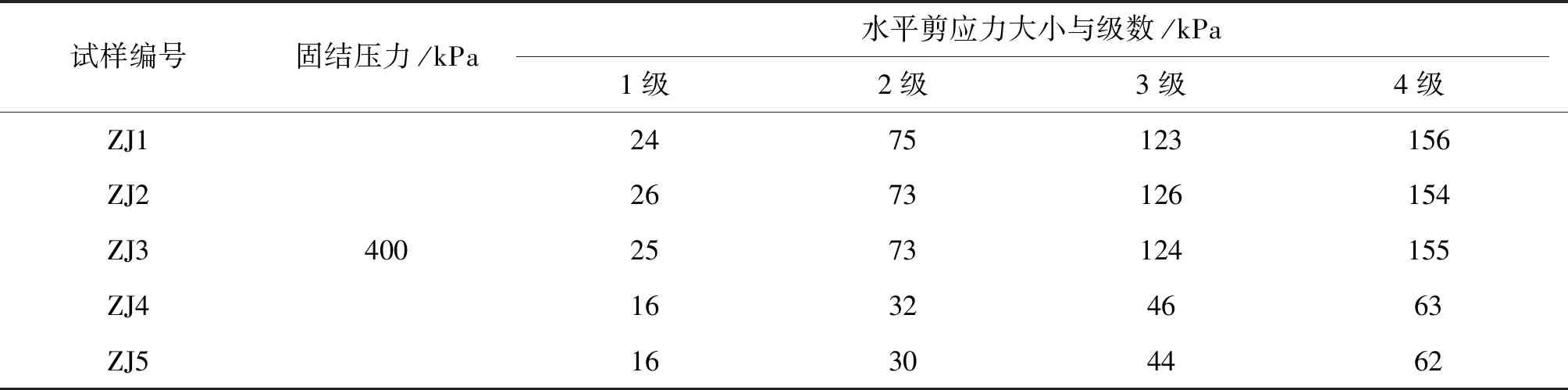
表2 不同含水量試樣的直剪蠕變試驗方案

1.2 試驗結果分析

所有流體在有相對運動時都要產生內摩擦力，這是流體的一種固有物理屬性，稱為流體的粘滯性或粘性[10].在直剪流變試驗條件下把土的粘滯系數定義為蠕變曲線圖上等速蠕變階段的剪應力與相應該曲線的剪切速率的比值[11].

η=τ/γ

圖3～圖6為不同結合水含量試樣的剪應變—時間關系曲線，圖7～圖11為各試樣的剪應力—剪應變等時曲線.基于試驗結果求得的各試樣平均粘滯系數列于表3之中.圖12為平均粘滯系數隨含水量變化的關系曲線.

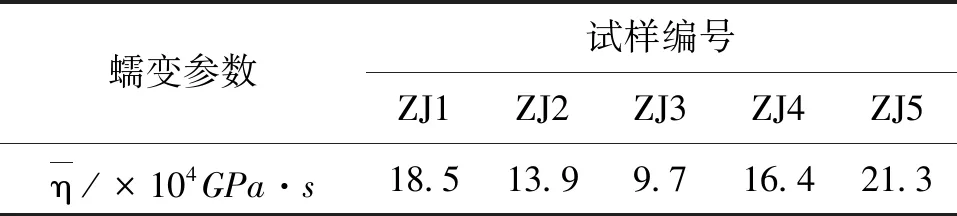
表3 不同結合水含量試樣的平均粘滯系數

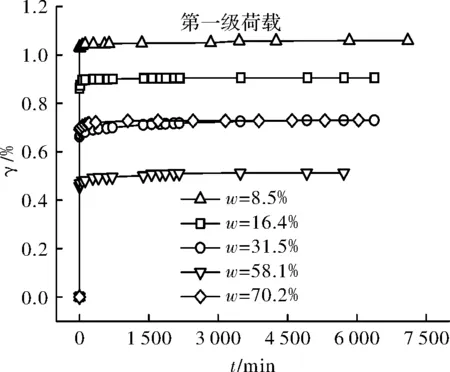
圖3 第一級荷載下不同含水量試樣的剪應變-時間關系曲線Fig.3 Shear strain time relation curve of samples with differentwater content under first stage load

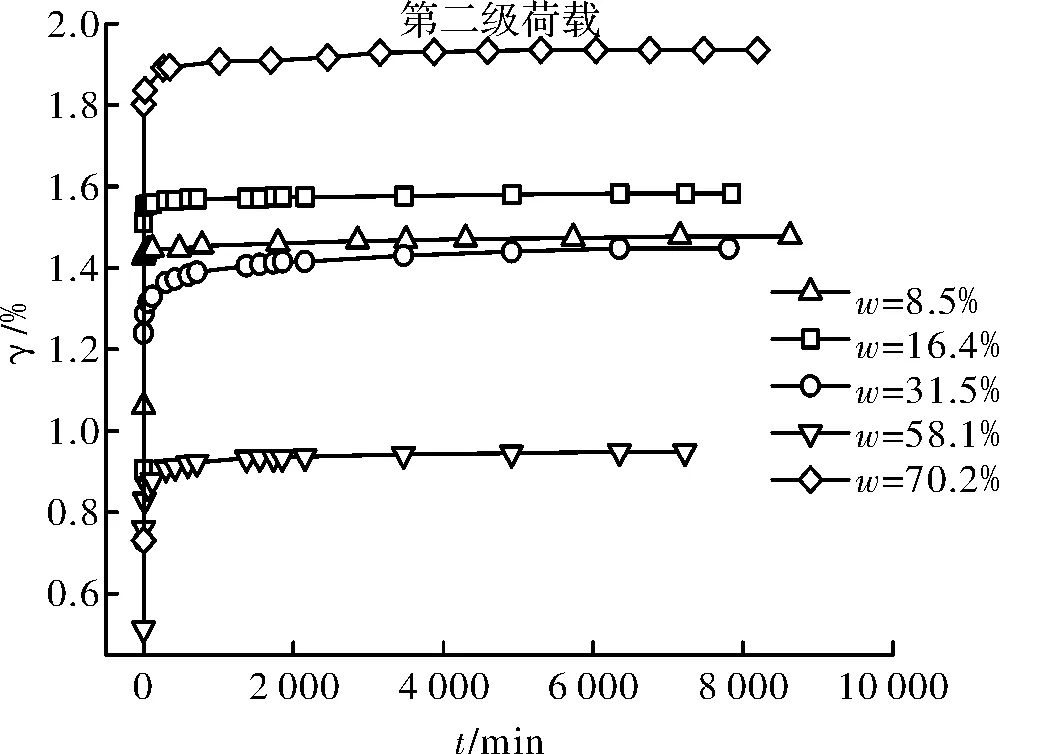
圖4 第二級荷載下不同含水量試樣的剪應變-時間關系曲線Fig.4 Shear strain time relation curve of samples with differentwater content under second stage load

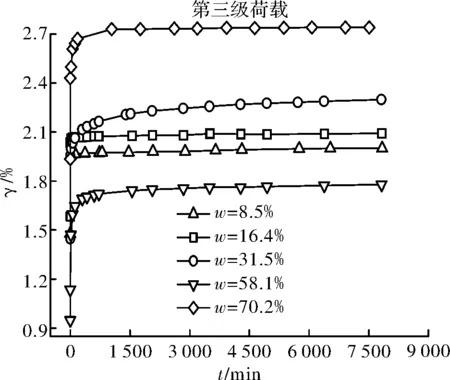
圖5 第三級荷載下不同含水量試樣的剪應變—時間關系曲線Fig.5 Shear strain time relation curve of samples with differentwater content under third stage load

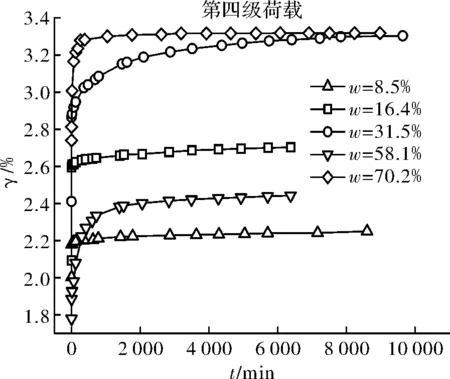
圖6 第四級荷載下不同含水量試樣的剪應變—時間關系曲線Fig.6 Shear strain time relation curve of samples with differentwater content under forth stage load

觀察圖3～圖6可以看出，不同含水量試樣的γ-t曲線均包括各級剪應力作用瞬間產生的瞬時變形和隨時間增長的時效變形，并且呈現出不同程度的上凸趨勢,保持應力不變的情況下,隨著時間的增加，變形也隨之增加直至穩定.其中，試樣ZJRB7-1(ω=8.5%=0.27ωp)由于其含水量相對較低，顆粒表面粗糙不平且僅存在強結合水，其水膜厚度較薄，在豎向壓力作用下顆粒緊密接觸，顆粒間范德華力作用比較強，土體變形阻力較大，在各級剪應力作用瞬間產生瞬時變形后，時效變形曲線接近水平，即時效變形隨時間發展不明顯，表現為穩定蠕變，同時從圖 7可以看出，相應的剪應力—剪應變等時曲線在低剪應力水平下重合度較高，在高剪應力水平下不同時刻的曲線簇才開始分開，但分開的幅度也不是十分明顯.試樣ZJ2(ω=16.4%=0.53ωp)的含水量仍低于其最大強結合水含量(wg≈0.885wP=27.1%ωg≈0.885ωp=27.1%)，但此時土顆粒表面吸附的強結合水膜較厚，顆粒間的范德華力作用被削弱的同時，排斥力作用被增強，土體變形阻力較試樣ZJ1要小，時效變形隨時間的增長較為明顯，隨著剪應力水平的提高，等速蠕變階段越來越明顯根據表3和圖12可知，試樣的平均粘滯系數隨著含水量的增加呈現出先逐漸降低至某一值后又逐漸增大的趨勢.當含水量小于其塑限含水量(ω≤ωp)時，土體中僅含結合水，其粘滯系數隨著含水量的增加逐漸減小，并在塑限含水量附近達到最小值，即隨著含水量的增加，土顆粒間的變形阻力在減弱，相應的蠕變速率在增加.當含水量超過其塑限含水量(ω>ωp)時，結合水和自由水同時存在于土體中，其粘滯系數隨著含水量的增加逐漸增大，即隨著含水量的繼續增加，試樣時效變形特性有所減弱.

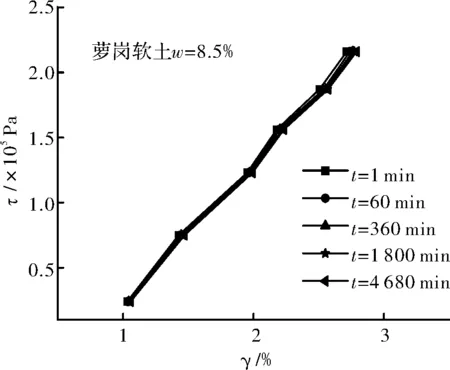
圖7 試樣ZJ1的剪應力—剪應變等時曲線Fig.7 Shear stress shear strain isochronous curve of sample ZJ1

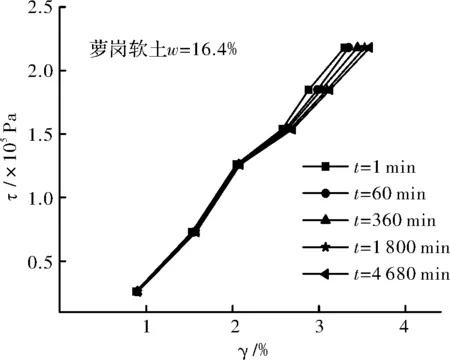
圖8 試樣ZJ2的剪應力—剪應變等時曲線Fig.8 Shear stress shear strain isochronous curve of sample ZJ2

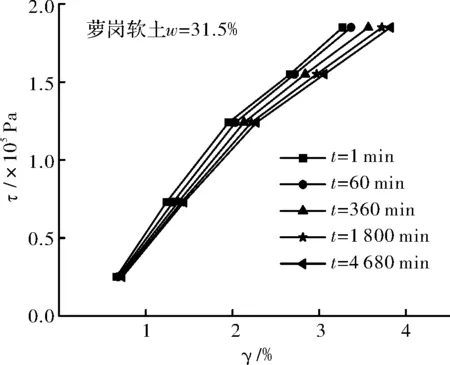
圖9 試樣ZJ3的剪應力—剪應變等時曲線Fig.9 Shear stress shear strain isochronous curve of sample ZJ3

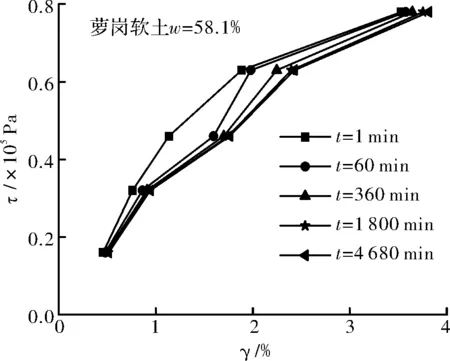
圖10 試樣ZJ4的剪應力—剪應變等時曲線Fig.10 Shear stress shear strain isochronous curve of sample ZJ4

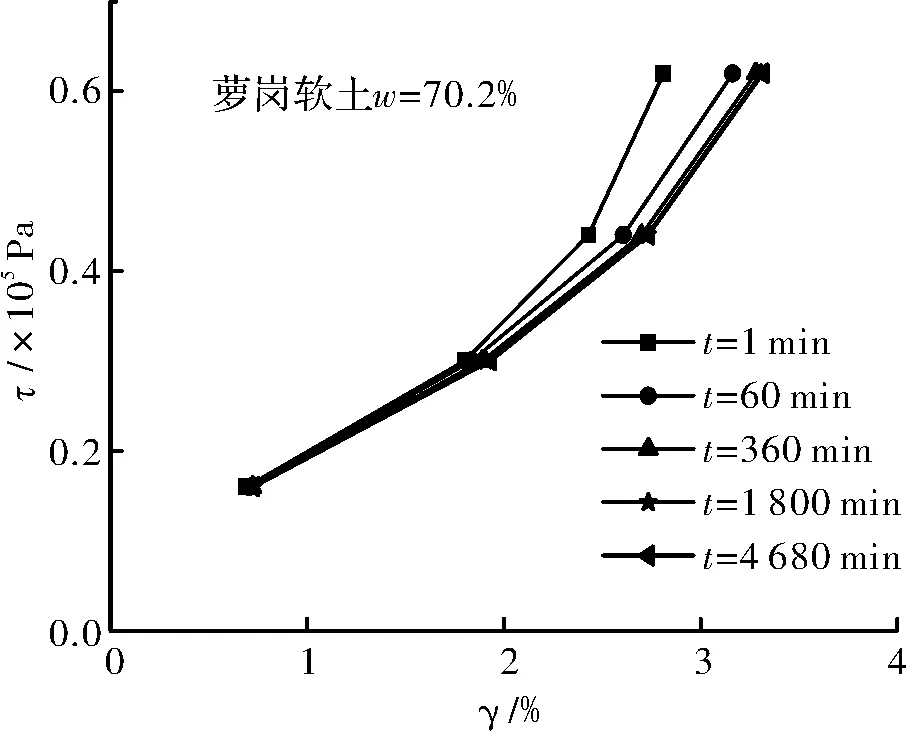
圖11 試樣ZJ5的剪應力—剪應變等時曲線Fig.11 Shear stress shear strain isochronous curve of sample ZJ5

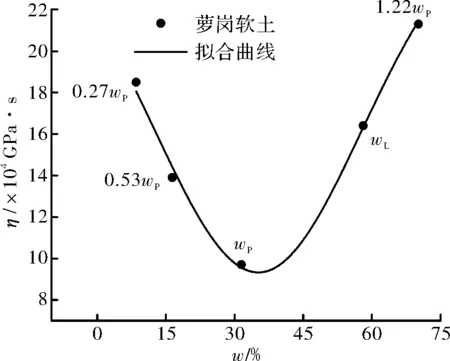
圖12 平均粘滯系數與含水量的關系曲線Fig.12 The relation curve of average viscosity coefficient and water content

以上充分說明了蘿崗軟土具有明顯的時效變形特性.

2 軟土流變模型

一般描述蠕變特性本構模型可分為經驗模型和元件模型[12].元件模型由胡克彈性體、牛頓粘滯體以及圣維南剛塑體等基本流變元件及其組合體組成，用于描述應力—應變—時間的關系.

根據前文分析，蘿崗軟土的典型蠕變曲線主要包括衰減蠕變和等速蠕變階段，因此，分別選取五元件廣義Kelvin模型和西原正夫模型對其進行分析.

2.1 廣義Kelvin模型

如圖13所示，廣義Kelvin模型由一個彈簧和兩個Kelvin體串聯而成，相應的蠕變方程為

γ(t)=J(t)τ

(1)

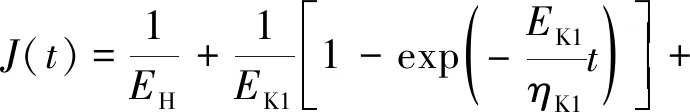
(2)

式中：EH為彈簧的彈性模量，ηK1、ηK2和EK1、EK2為Kelvin體的粘滯系數和彈性模量，t為時間，τ則為相應剪應力.

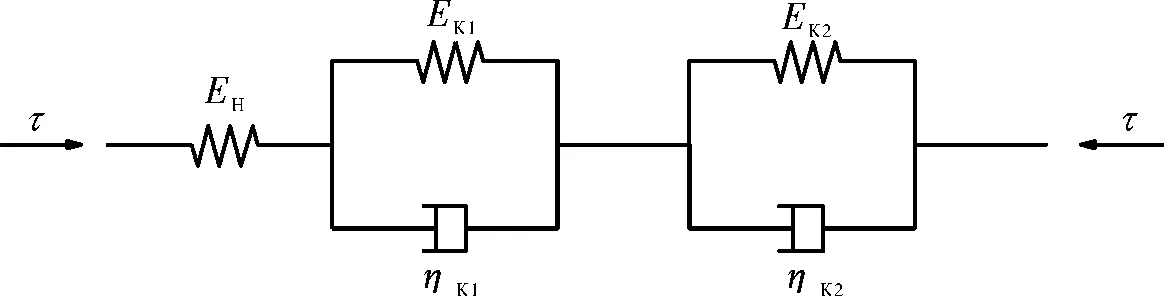
圖13 廣義Kelvin模型Fig.13 Generalized Kelvin model

上述模型中共有5個待定參數EH、ηK1、ηK2、EK1和EK2，利用OriginPro 8中的Associate函數對相應試驗數據進行擬合，Associate函數關系式為

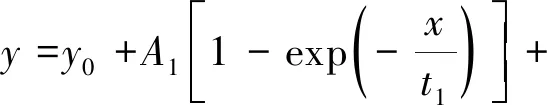
(3)

式中，y0、A1、t1、A2和t2均為擬合參數.對比式(1)、(2)和(3)可得：

進行相應轉換，則

2.2 西原正夫模型

如圖14所示，西原正夫模型是由Kelvin模型與Bingham模型串聯得到的，其本構方程為

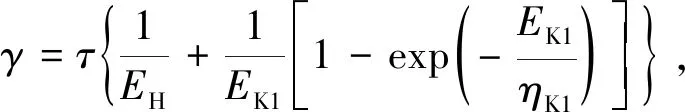
(4)

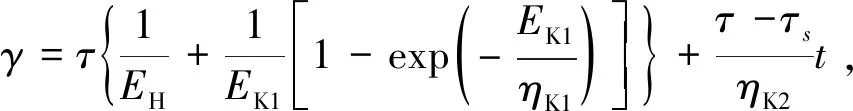
(5)

式中，EH為彈簧的彈性模量，ηK1和EK1為Kelvin體的粘滯系數和彈性模量，ηK2和τs為Bingham模型中的粘滯系數和摩擦阻力，t為時間，則為相應剪應力.

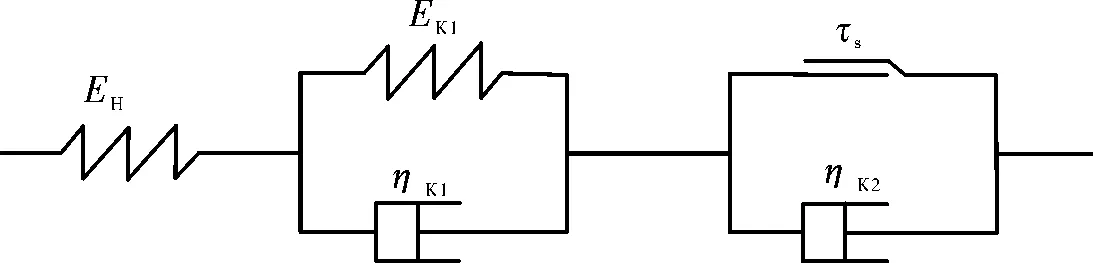
圖14 西原正夫模型Fig.14 Nishihara Masao model

上述模型中共有5個待定參數EH、ηK1、ηK2、EK1和τs，可利用OriginPro 8中的自定義函數進行擬合.因為含水量為8.5%、16.4%、31.5%的試樣各級應力值基本相同，故為減少自定義函數的數量，在定義函數時將含水量8.5%、16.4%、31.5%的試樣在各級應力下的值取為相同的.同理58.1%、70.2%為一組.各組含水量試樣直剪蠕變方案具體見表4.相應擬合結果如表5、表6所示.

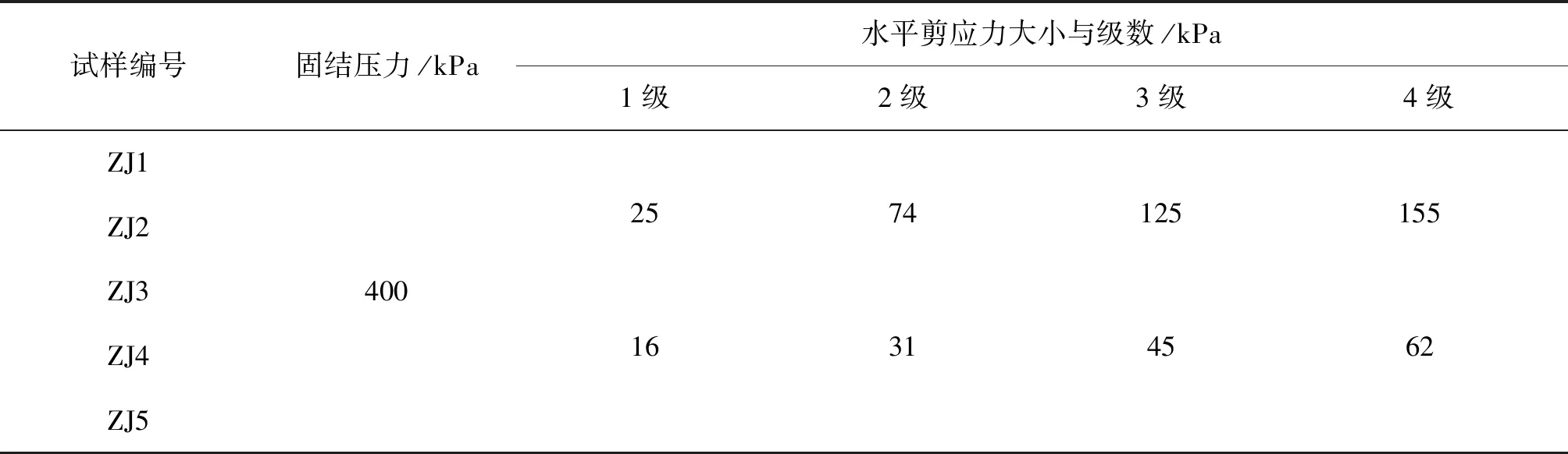
表4 各組含水量試樣的直剪蠕變試驗方案

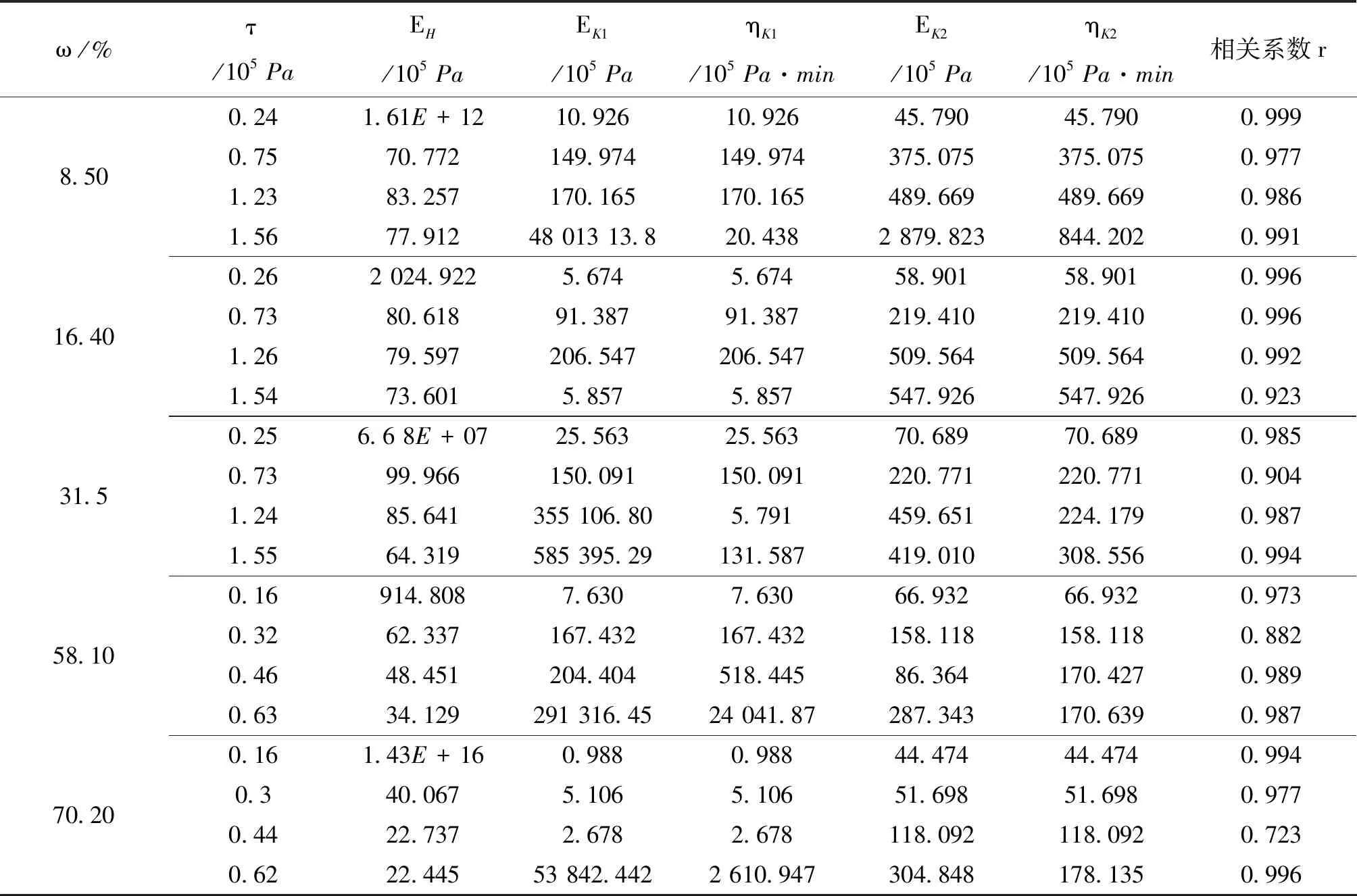
表5 五元件廣義Kelvin模型中各組合對應的模型參數表

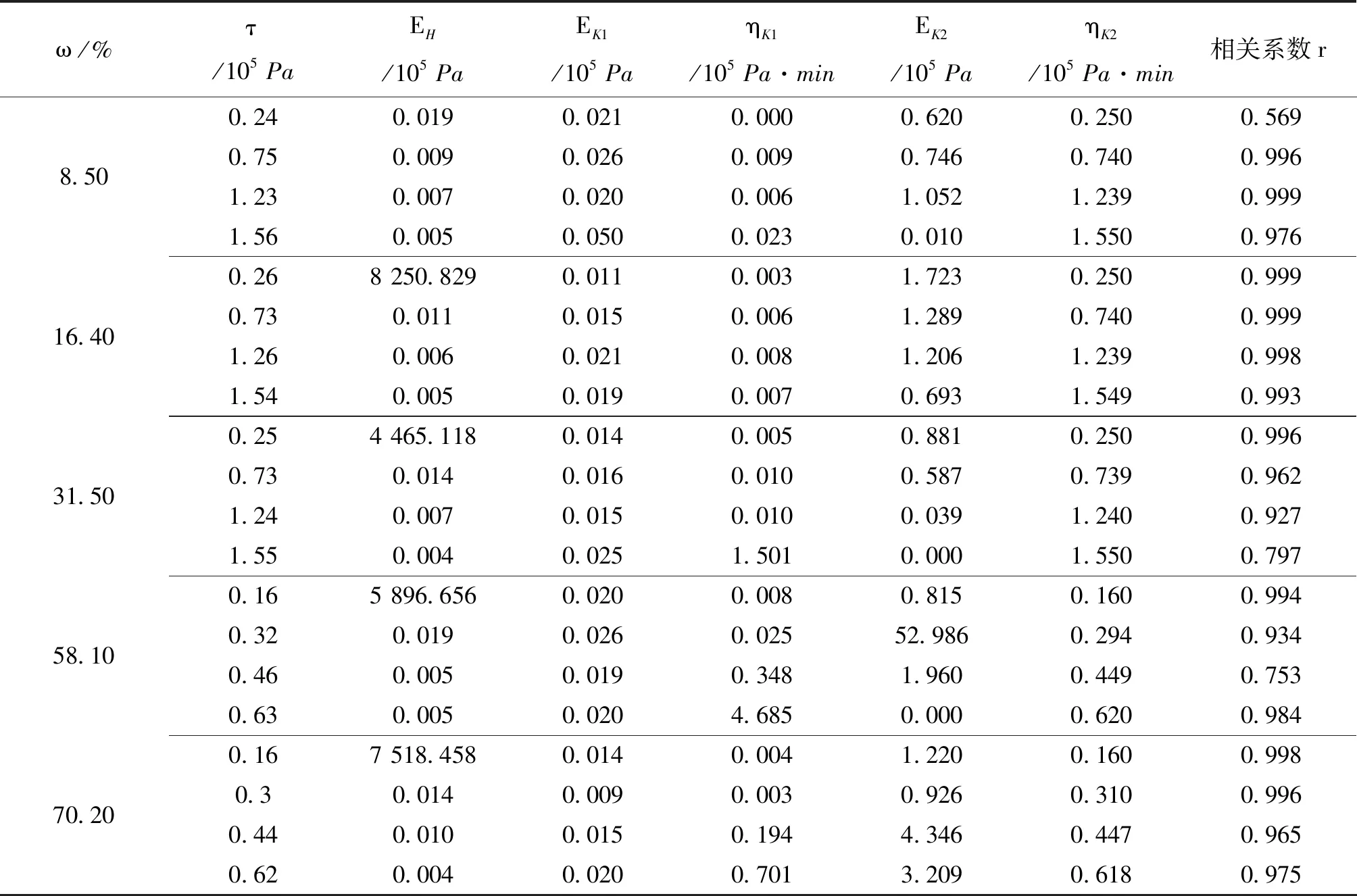
表6 西原正夫模型中各組合對應的模型參數表

3 理論模型擬合分析與評價

觀察表5可以看出，五元件廣義Kelvin模型在各含水量各荷載組合下的擬合程度都較高；當含水量為8.5%時，各應力水平下擬合程度都較高，相關系數在0.94～0.99之間；在16.4%、31.5%、58.1%、70.2%含水量下都有一個擬合程度較差的組合，且隨著含水量的升高，相關系數由0.92、0.90、0.88至0.72遞減.

觀察表6可以看出，西原正夫模型在各含水量各荷載組合下的擬合程度較高， 但在第一級荷載，8.5%含水量的組合下擬合較差，相關系數僅為0.56，擬引入鄧肯-張模型非線性E-v模型嘗試對西原正夫模型進行修正.

對比表5和表6可知，兩個模型有較好的互補性.五元件廣義Kelvin模型擬合較差時，西原正夫模型在對應的的組合下的擬合程度都較高，相關系數在0.93～0.99之間.而西原正夫模型擬合較差的組合，五元件廣義Kelvin模型擬合的相關系數在0.98～0.99之間.

如圖15～圖22所示，五元件廣義Kelvin模型的擬合曲線在各組合下的彈性變形階段和衰減蠕變階段都能準確的描述，但隨著時間的增加，只有在第四級荷載下的ZJ4(58.1%)、ZJ5(70.2%)試驗依舊能很好的擬合，其余試樣在各級荷載下，擬合曲線的最終變形都低于實際的試驗結果；ZJ2(16.4%)、ZJ4(58.1%)、ZJ5(70.2%)試樣在各級荷載作用下的試驗結果用西原正夫模型擬合在各個階段都能準確的描述，ZJ1(8.5%)用西原正夫模型進行擬合，在較高應力時擬合效果較理想，而第一級荷載時擬合效果不理想，彈性階段小于實際的試驗結果，而最終變形則過大，ZJ3(31.5%)在各級荷載的擬合效果都較好，但隨著應力的增加，擬合曲線在彈性變形階段高于實際試驗結果，衰減蠕變階段則較小，最終變形則較大.

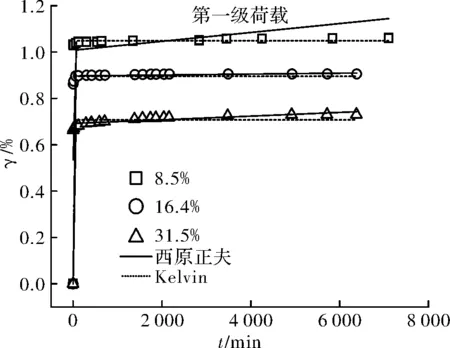
圖15 第一級荷載、各含水量不同模型擬合對比Fig.15 The first load, each water content of differentmodels fitting comparison

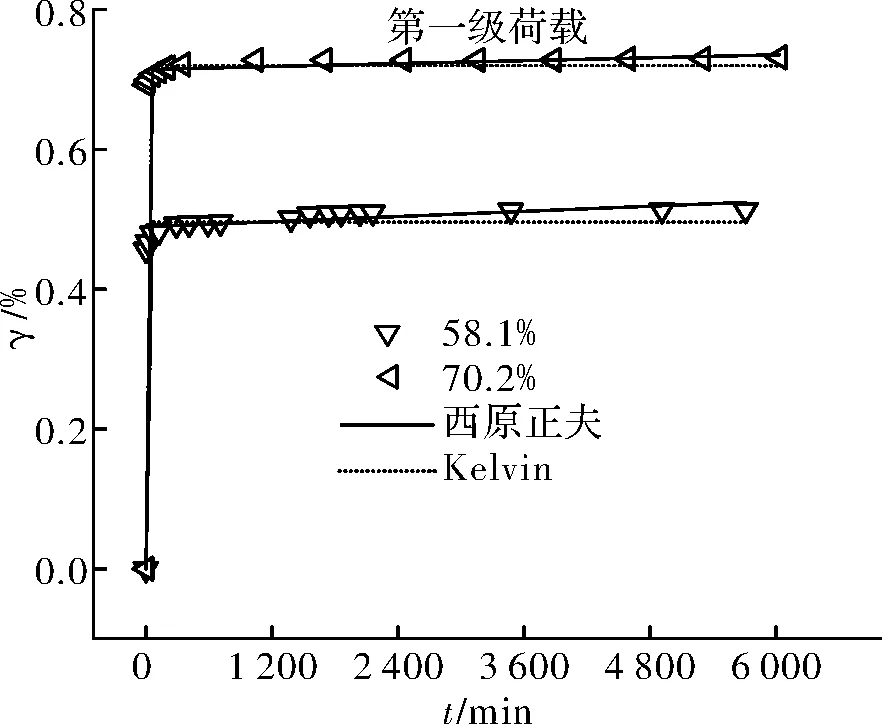
圖16 第一級荷載、各含水量不同模型擬合對比Fig.16 The first load, each water content of differentmodels fitting comparison

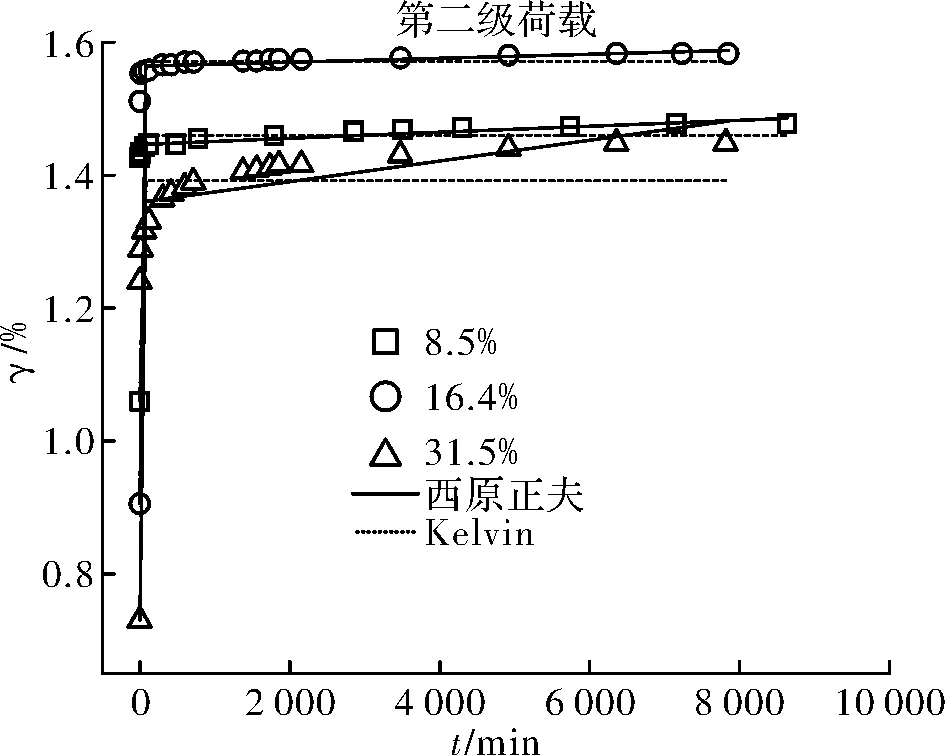
圖17 第二級荷載、各含水量不同模型擬合對比Fig.17 The second load, each water content of differentmodels fitting comparison

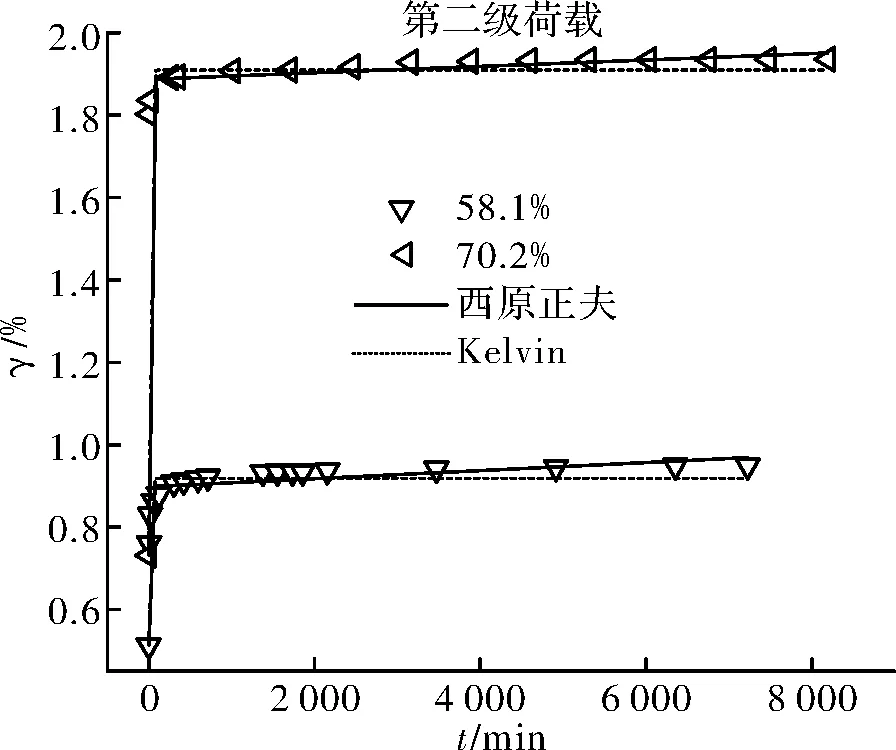
圖18 第二級荷載、各含水量不同模型擬合對比Fig.18 The second load, each water content of differentmodels fitting comparison

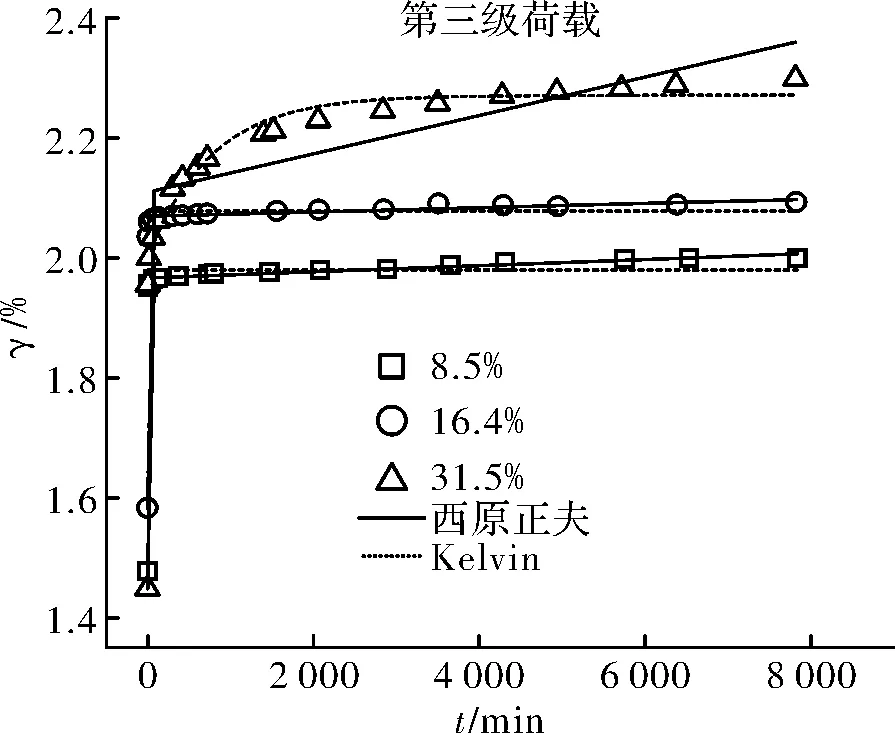
圖19 第三級荷載、各含水量不同模型擬合對比Fig.19 The third load, each water content of differentmodels fitting comparison

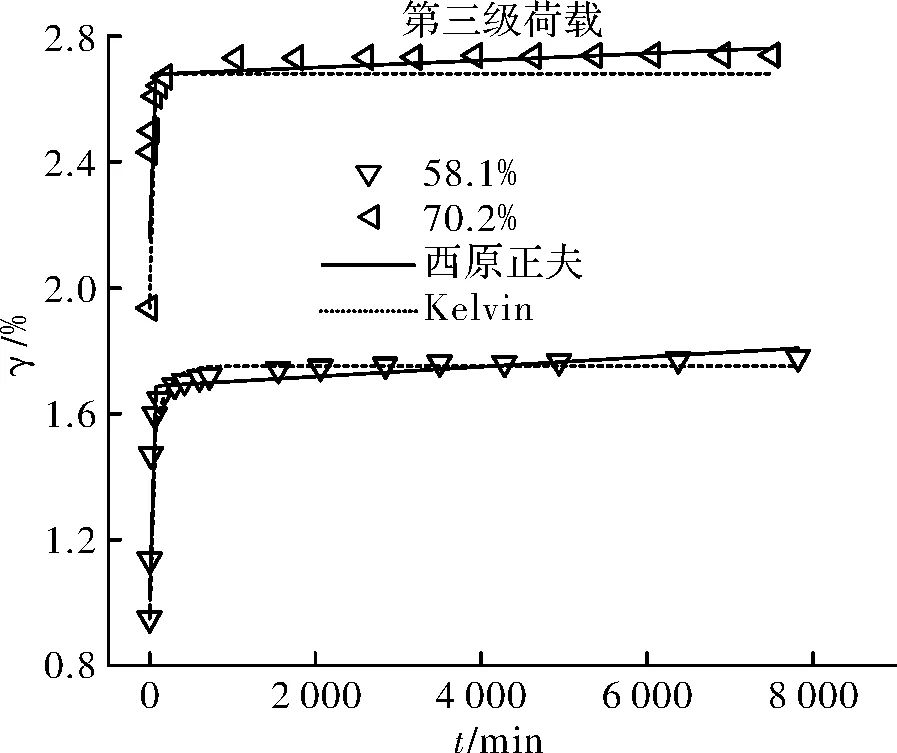
圖20 第三級荷載、各含水量不同模型擬合對比Fig.20 The third load, each water content of differentmodels fitting comparison

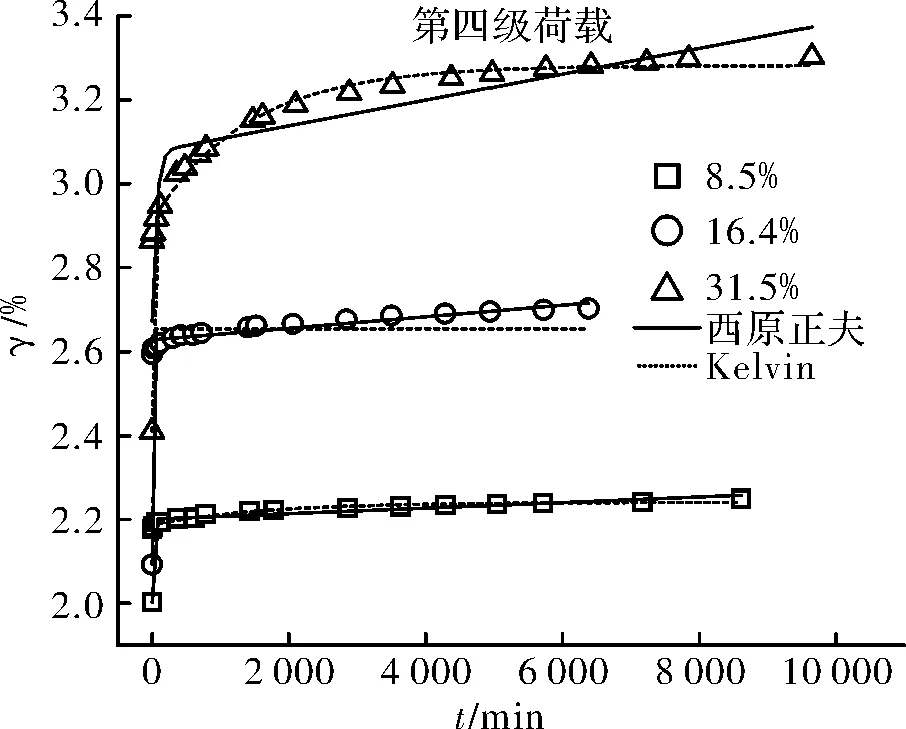
圖21 第四級荷載、各含水量不同模型擬合對比Fig.21 The forth load, each water content of differentmodels fitting comparison

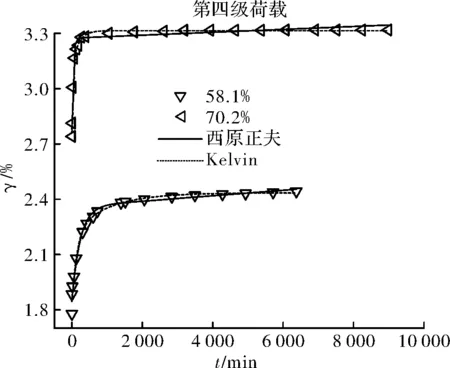
圖22 第四級荷載、各含水量不同模型擬合對比Fig.22 The forth load, each water content of differentmodels fitting comparison

4 引入鄧肯—張非線性模型

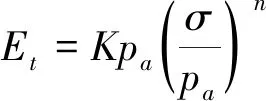
其本構方程為

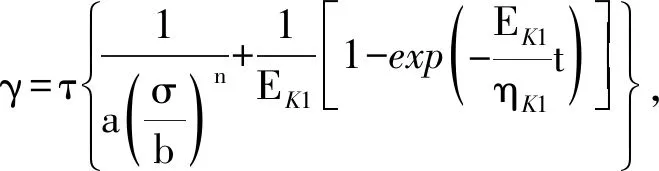
(6)

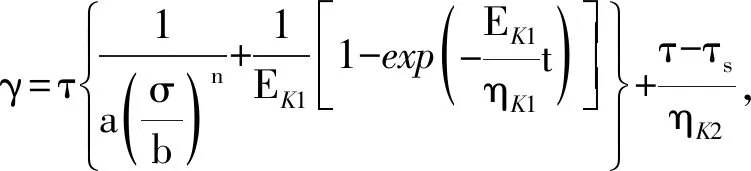
(7)

式中：a、b、n為鄧肯-張模型參數，σ為豎向應力，ηK1和EK2為Kelvin體的粘滯系數和彈性模量，ηK2和τs為Bingham模型中的粘滯系數和摩擦阻力，t為時間，τ則為相應剪應力.

以含水量為8.5%、第一級荷載的試樣為例，根據修正后的模型和本構方程對蠕變試驗曲線進行擬合，并與線性的西原正夫模型進行對比，如圖23所示，具體擬合參數見表7.

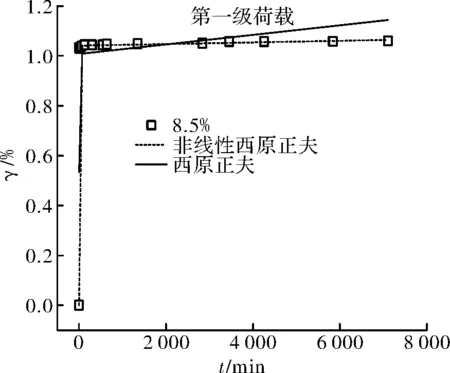
圖23 線性與非線性西原正夫模型擬合對比圖Fig.23 Contrast diagram of linear and nonlinearNishihara Masao model

表7 非線性西原正夫模型參數表

修正后的模型擬合與試驗結果具有良好的一致性，在各個階段都能較準確的描述軟土的時效變形，相關系數由線性的0.56變為0.99，遠優于線性的西原正夫模型.可見基于鄧肯-張非線性彈性的西原正夫模型可用于描述低應力水平、低含水量狀態的軟土時效變形特性.

5 結論

(1)不同含水量的珠三角軟土直剪蠕變試驗結果表明，珠三角軟土具有明顯的變形時效性，且含水量對軟土時效變形特性產生重要影響，隨著含水量的增加，軟土的蠕變達到穩定時的變形增大.由于結合水膜厚度變化引起的顆粒間范德華力和排斥力主導地位的交替和自由水對顆粒間錯動滑移和摩擦作用的影響，試樣的平均粘滯系數隨著含水量的增加呈現出先逐漸減少至某一值后又逐漸增大的趨勢.

(2)五元件Kelvin模型與西原正夫模型都能較好的描述大多數含水量和應力水平組合下的軟土時效變形特性.兩者有良好的互補性，相結合可以更合理地對軟土時效變形曲線進行擬合.

(3)基于鄧肯-張非線性彈性的西原正夫模型可以更合理地描述低應力低含水量下的軟土時效變形特性.