基于儀表檢定參數的測量值修正和校準

劉傳龍 李四海

（十堰市產品質量監督檢驗所，湖北十堰 442000）

0 引言

所有測量儀表、傳感器（變送器）和計量器具的測量結果數據都不同程度的存在系統誤差和隨機誤差，其中隨機誤差幾乎是不可改變的，但系統誤差則可通過代數運算的方法加以修正和校準。當系統誤差的存在影響到科學測試應用的基本技術要求時，則有必要對測量結果數據的系統誤差進行修正和校準。測量結果數據的修正可以由測量儀表（器具）使用者識別并手工修正；而測量結果數據的校準則復雜一些：早期完全由測量儀表（器具）使用者以高等級儀表檢定數據為參考值進行手工計算校準。目前隨著儀表智能化技術的發展提高，也有測量儀表制造者以提供檢定數據輸入端口，僅讓使用者參與數據輸入，然后后由儀表內部程序自動完成的方式進行校準。

1 儀表檢定數據的修正參數

1.1 修正值、修正因子的定義

按照JJF1001-2011《通用計量術語及定義》中5.7節-注2、3條定義：（1）修正值是用代數方法與未修正測量結果相加，以補償其系統誤差的值，修正值等于負的系統誤差的估計值；（2）修正因子是為補償系統誤差，與未修正測量結果相乘的數字因子。

1.2 修正值、修正因子的作用

（1）消除儀器設備的固有系統誤差采用修正值修正測量值；（2）消除與測量值（量程）比例相關的系統誤差采用修正因子修正測量值。

1.3 修正值、修正因子的簡單識別方法

（1）識別修正值、修正因子的數據來源：由儀器或設備的檢定（校準）證書提供的一組“示值誤差”或者“示值相對誤差”數據。

（3）實際的修正值δ識別中，δ與檢定證書中“示值誤差”相關。可用“示值誤差均值”作為“系統誤差的估計值”，即：

它是一個有符號（可正可負）數字因數。按公式（1）識別δ具有最佳修正效果；但為避免繁瑣計算，δ可簡化選取示值誤差（X-X）的“中間、中位值和零點誤差值”，也有不錯的修正效果。

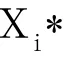
（4）實際的修正因子φ識別中，φ與檢定證書中“示值相對誤差”相關。φ一般取“1與合適的示值相對誤差q之差”，所謂“合適”，可考慮幾個選項：（a）一致性較好的示值相對誤差；（b）最小的示值相對誤差；（c）最大測量點的示值相對誤差。

如果已識別確定某個q值來關聯修正因子φ，根據相對示值誤差的定義，自然考慮修正運算式為：

表1 檢定結果數據

表2 型號WSM-100拉壓力試驗機檢定證書數據進行修正值δ識別/修正

表3 型號WSM-100拉壓力試驗機檢定證書數據進行修正因子φ識別/修正

由于q值可正可負，且q的絕對值遠小于1，所以1-q是一個接近于1（大于1或者小于1）的數字因子。修正因子使用（修正）方法：修正后測量值X*等于未修正測量值X乘以修正因子φ，即：

2 單測量點檢定數據的修正值δ識別

指標準砝碼類（或某些刻度類量器），檢定（校準）證書中已明確標明一個有符號的參數為“示值誤差”：此種情形可直接將這個示值誤差直接識別為修正值δ。具體修正公式：修正后測量值X*=未修正測量值X-δ。

實例：以我單位編號SM036：LT101電子天平用500g標準砝碼2018年檢定結果數據見表1：

實際分度值/d0.1g；檢定分度值/e1g；最大稱量/g500g。

修正值識別為：δ=+0.1g

3 多測量點（一個量程范圍）權威資質機構檢定數據的修正值δ識別原理

儀器或設備檢定（校準）證書提供了一組（多個測量點）數據，而且附有一組示值誤差（或相對示值誤差）參數值。修正參數識別時，儀表設備多點檢定數據通常在“標準值（橫坐標）——測量值（縱坐標）坐標系”中描述，如圖1所示。

圖1 多測量點條件下修正值δ識別示圖意

圖2 多測量點條件下一般測量數據分布狀況

4 多點測量數據的修正值/修正因子識別實例

（1）以我單位檢定證書編號：20170808247，型號WSM-100拉壓力試驗機檢定證書數據進行修正值δ識別/修正見表2。

（2）同樣以我單位檢定證書編號：20170808247，型號WSM-100拉壓力試驗機檢定證書數據進行修正因子φ識別/修正實例見表3。

5 修正值δ和修正因子φ識別的通用最優方法

（1）考慮檢定數據在“標準值（橫坐標）——測量值（縱坐標）”坐標系中的直線模型表達。如圖2所示。

圖2中假定檢定數據的修正前最佳擬合直線方程為：X=ΨX＋δ，圖中數據為一般情形：即示值誤差均值為正，最佳擬合直線斜率大于1。有先驗的算法（最小二乘法）可知：擬合直線的兩個參數分別按下述公式計算：

圖3 多測量點條件下修正值修正過程示意圖

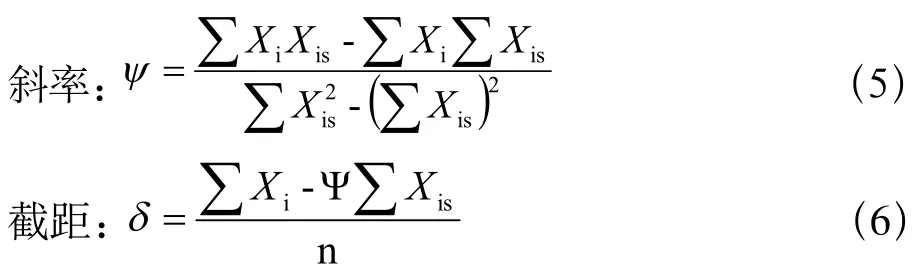
修正值δ與為擬合直線的截距相等。

修正因子φ為擬合直線斜率Ψ的倒數：

6 參考第四節中描述的過程，分兩步對測量值進行修正

第一步，先將擬合直線在縱軸的截距識別為修正值δ是合理的，將每個測量值減去修正值δ，即：

如圖3所示：測量數據點全體向下移動距離δ，最大示值誤差△大幅度降低。

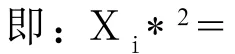
如圖4所示：修正后擬合直線與理想測量直線重合，最大示值誤差△進一步降低。

（1）很明顯，如果使用修正值δ、修正因子φ同時修正的通用方法，需要比較繁瑣的計算過程，而且按最小二乘法擬合直線求得的修正參數δ和φ（φ=1/Ψ）是最佳修正參數，它一般適用于帶有計算機數據采樣的傳感器校準，測量設備制造商把這種修正過程編制為專門的傳感器標定程序，設備使用者定期依據檢定部門現場檢定數據，直接啟動標定程序界面，錄入檢定數據后，計算機自動進行計算和修正，完成修正校準后可以極大地改善傳感器測量精度。作為檢定部門一般不推薦使用，而使用近似的和單一的（修正值δ、修正因子φ選其一）識別方法已可滿足要求。

圖4 多測量點條件下修正因子修正過程示意圖

圖5 將測量值校準到校準直線上

（2）有的測量儀器帶有“零點校正”功能，實際上就是把空載測量值（零點示值誤差）識別為修正值δ，相當于一種由使用者操作的儀器自帶修正值識別功能。

（3）對于多測量點檢定數據，如果僅進行修正值δ識別，也就是擬合直線模型為：X=X+δ，此時根據公式（5）、（6），由于Ψ=1，得：

圖6 折線校準法示意圖

（4）如果僅進行修正因子φ識別，也就是擬合直線模型為：X=φX，則相當于本節所述通用最優方法中另一種將修正值δ預設為“0”的特例。

7 儀器、傳感器（變送器）和計量器具的校準方法

儀器、傳感器（變送器）和計量器具檢定數據校準與修正的區別：校準參數在“測量值（橫坐標）——標準值（縱坐標）”坐標系下表達，與修正參數表達坐標系的自變量、因變量定義則相反。

7.1 直線校準法的校準參數

（3）按上條目標函數要求，可以得到的推導結果是：

7.2 折線校準（或稱分段校準）法的校準參數

（1）當儀表儀器測量值與標準值之間的示值誤差在某些量程或測量點比較大，但重復性較好時有必要選擇折線校準法。把每兩個相鄰標準值測量點之間連接為（n-1）段折線，將每段折線都當成校準直線使用。如圖6所示。

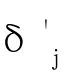
校正值：

8 結語

（1）采用近似識別方法時，一般以“示值誤差”（X-X）為依據識別修正值δ；以“示值相對誤差”{q=（X-X）/X}為依據識別修正因子φ。（2）在從檢定（校準）證書中識別選取“示值誤差”和“示值相對誤差”時，注意不要丟失正負號。（3）儀器設備檢定后等級已滿足使用要求的前提下，修正值δ和修正因子φ都可以不用識別。（4）采用修正值/修正因子均可以有效地縮小最大示值誤差△，或者說可以改善測量不確定度。（5）修正因子φ的選擇需要慎重，一般應選擇除零外最小或者次小的示值相對誤差q來計算φ，最大測量點的示值相對誤差q通常滿足該條件；識別最大測量點示值相對誤差為修正因子的方法有時又稱“滿量程校正”法。（6）采用最優識別方法時，用最小二乘法擬合直線方程：X=ΨX＋δ，截距δ與修正值等價相關，斜率Ψ的倒數與修正因子φ等價相關。（7）實際應用中，修正值δ和修正因子φ兩者選其一即可，而且一般采用近似識別方法。如果修正值δ和修正因子φ同時采用，一般分兩步進行，先按公式：X*=X-δ完成修正值δ修正，再按公式：X*=X*×φ完成修正因子φ修正。（8）校準參數校準值δ'和校準因子φ'對測量點數據進行校準可以采用公式：X*=φ'X+δ一步完成校準。（9）最優修正參數與最優校準參數有類似的表達形式，它們之間差異的原因來自選擇不同的擬合直線模型以及不同的表達坐標系，可以說它們是一個問題的兩種表達形式。