速度與準確率權衡：被試反應狀態評價與建模 *

郭小軍 羅照盛

(江 西師范大學心理學 院，南昌 330022)

1 前言

反應時與準確率的關系是認知心理學的重要研究領域（Heitz, 2014; Ratcliff, Smith, Brown, &McKoon, 2016; Wickelgren, 1977）。在認知實驗中，影響反應時與準確率關系的兩個主要方面是認知能力或者信息加工效率（Wenger & Gibson,2004; Wenger & Townsend, 2000）以及速度與準確率權衡（the speed-accuracy tradeoff, SAT; Donkin,Little, & Houpt, 2014; Ratcliff et al., 2016）。認知能力或信息加工效率越高，反應時越短，準確率越高；而速度與準確率權衡指被試有時會以犧牲準確率為代價換取加工速度，有時候會以犧牲加工速度為代價換取準確率提升（朱瀅, 2009）。在行為實驗中，速度一般用反應時作為指標，速度越快，反應時越短；反之，反應時越長。所以，認知實驗的速度與準確率權衡就是反應時與準確率權衡。

在認知心理學中，研究被試的速度與準確率權衡通常以操作不同獎勵措施或者反應時限制進行。這類研究在不同領域已有了大量的研究成果，特別是基于速度與準確率權衡模型（the speedaccuracy tradeoff model, SAT 模型 ; Reed, 1973;Wickelgren, 1977）上進行的研究，如概念加工（ McElree, Jia, & Litvak, 2000）， 句 子 理 解（McElree, 2000; McElree, Foraker, & Dyer, 2003），記憶（McElree, 1998），注意（Giordano, McElree,& Carrasco, 2009; McElree & Carrasco, 1999）等領域。在不同實驗條件下，通過對SAT 模型中的參數組合進行變化，然后計算模型與數據擬合的R2指數（Reed, 1976），最后確定最佳的參數組合形式。這些研究發現SAT 模型都能較好地擬合速度 與 準 確 率 權 衡 數 據 （ Reed, 1973; Wickelgren,1977）。

SAT 作為影響反應時與準確率關系的重要因素，不僅對認知實驗有著重要的影響，在認知能力測驗中也同樣不可忽視（Goldhammer, Naumann,& Greiff, 2015; van der Linden, 2009; van der Maas,Molenaar, Maris, Kievit, & Borsboom, 2011）。認知能力測驗的加工任務比認知實驗任務更為復雜，通常也不會采用人為的實驗控制（強調速度或者準確率，或者進行反應時限制）方法對SAT 現象進行研究。在認知能力測驗過程中，被試往往需要在有限的時間內完成測驗作答，此時就需要在反應時與準確率之間進行權衡。這種權衡影響被試在項目上的作答反應時是否充足，進而對準確率產生不同的影響。

在認知能力測驗中，對反應時與準確率聯合分析的常用模型是 van der Linden（2007）提出的分層模型。分層模型由兩層構成，第一層為獨立的反應時與反應模型，第二層是被試速度與能力的聯合分布以及項目參數間的聯合分布。分層模型僅通過被試能力與速度之間的相關來反映反應時與準確率的權衡關系。Meng，Tao 和Chang（2015）用項目水平與被試水平的交互效應來解釋反應時與準確率的關系，卻無法反映反應時與準確率的動態權衡。Bolsinova，De Boeck 和 Tijmstra（2017）從項目水平角度，以殘差反應時作為協變量引入反應模型中來反映反應時與準確率的權衡效應；Bolsinova，Tijmstra 和 Molenaar（2017）進一步擴展到被試水平，但是都過度擴大了反應時對準確率的影響。被試在項目上的作答準確率是能力與反應時雙重作用的結果，能力決定了被試在項目上作答準確率的高度，而反應時則影響被試能否達到該準確率高度的重要因素。同時，Chen，De Boeck，Grady，Yanga 和 Waldschmidt（2018）通過作圖發現，反應時與準確率在不同認知能力測驗中并不是簡單的單調遞增關系，也有可能是先遞增后遞減的非單調趨勢。

對于反應時與準確率的關系，認知實驗通常認為隨著反應時的增加，準確率是逐漸遞增的，直到最高漸近線水平。但有的認知實驗如再認實驗，由于工作記憶的衰減和損耗，隨著反應時的增加，會降低準確率。認知能力測驗與認知實驗的測試形式是明顯不同的，并不存在學習效應，工作記憶衰減的影響較弱，這種遞減趨勢更可能受到項目難度、能力水平、速度水平或者能力與速度補償效應的影響。基于此，本文結合認知實驗SAT 模型與分層模型，分別構建了基于能力水平、速度水平和速度與能力相互補償的SAT 分層模型，探討認知能力測驗中反應時與準確率的非單調關系。

2 SAT 分層模型

在SAT 模型基礎上，通過理論邏輯分析，并加入能力、速度以及能力與速度的補償效應，構建三個SAT 反應模型，使其能夠反映能力、速度以及能力與速度補償效應在反應時與準確率動態權衡關系中的作用，并聯合反應時模型構成分層模型第一層；同時根據被試參數的聯合分布與項目參數的聯合分布構建分層模型的第二層，形成不同的SAT 分層模型。

2.1 反應時模型

在SAT 分層模型中，反應時采用對數正態反應時模型（van der Linden, 2007），見公式 1：

2.2 反應模型

Reed（1973, 1976）提出了反應時與準確率權衡關系的函數模型，見公式2：

在公式2 中， λ是漸近線水平參數，指在反應時無限制條件下，被試能達到的最高辨別力水平；φ 是辨別力水平隨著反應時變化的變化速率，反映函數曲線的陡峭程度； (t -)項指被試作答反應時與非決策反應時之差。

以能力水平的SAT 反應模型為例，在認知能力測驗情境下對公式2 進行了重構。首先， λ在認知實驗中定義為作答反應時不受限制時，被試在項目上能達到的最高辨別力，即作答準確率，這與項目反應理論模型的假設一致，即測驗無時間限制。于是，不同被試在不同項目上的最高準確率 λ定義為（公式3）：

aj是 項目區分度參數， bj為項目難度參數，i則為被試的能力參數，ij為被試作答反應時不受限制時的理論反應。

依據SAT-M1 構建的原理，同時構建了基于速度的SAT-M2 模型（公式6, M2）和基于能力與速度補償的 SAT-M3 模型（公式 7, M3）。

上述三個反應模型是基于相同思路、不同的因素進行構建的。在不同項目上，反應時與準確率并不是獨立的關系，被試的不同權衡狀態會影響被試在項目上的作答反應時，進而影響被試在項目上的作答準確率。由于受到權衡狀態的影響，項目的作答反應時與準確率并不總是單調關系，也可能存在非單調關系，同時非單調關系受到項目性質的影響。因此，在SAT-M1 模型中，對工作量參數 中等以下，同時難度參數中等的項目，此時被試可能愿意選擇花費更多的反應時作答該項目，由于受到自身能力水平的限制，隨著反應時增加，項目作答準確率增加到一定程度后，反而呈現下降趨勢。對于SAT-M2 模型，反映了工作量參數 超出了自身速度水平的項目上，如果被試選擇花費更多的反應時作答該項目，準確率會呈現先提高后下降趨勢。在SAT-M3 模型中，則兼顧考慮項目難度與工作量參數影響，對有些項目，被試作答準確率并不會隨著反應時增加達到最高準確率水平，反而會在最后呈現下降趨勢。在其他情況下，反應時與準確率更可能是單調遞增關系。

2.3 分層建模

在分層模型中，將對數正態反應時模型（公式1）與SAT-M1、SAT-M2 和SAT-M3 構成分層模型的第一層；能力參數與速度參數聯合分布（公式8）以及各項目參數聯合分布（公式9）構成分層模型的第二層。van der Linden 分層模型（M0）則是將對數正態反應時模型與公式3（為觀測變量，且加入猜測參數c），并聯合公式8-9 構成。

3 參數估計與模型選擇

3.1 模型的識別

為了能夠對模型進行識別，需要對模型一些參數進行限制。在本研究中，對三個SAT 分層模型的被試參數 和 固定均值為0，標準差為1。

3.2 貝葉斯參數估計

對三個SAT 分層模型所有參數，本文采用軟件JAGS 默認的Gibbs 取樣對被試與項目參數進行估計。在SAT 分層模型中，各項目參數的先驗分布分別為：aj，1/σj以及 αj都服從大于 0 的左截尾正態分布N（0,1）I（0,），猜測參數cj為beta（5,17）分布，項目參數bj與βj的均值向量μI服從二元正態分布，協方差矩陣ΣI服從逆威沙特分布InvWishart（R2,2），R2為二元對角矩陣。

對于被試參數，由于約束條件限定σθ2=1 以及στ2=1，因此能力與速度參數的協方差與相關系數相等，即 ρθτ=σθτ，并且 ρθτ∈[-1, 1]。ρθτ的先驗分布采用雙側截尾的正態分布 ρθτ～N（0, 1）I（-1, 1）。

3.3 模型選擇

在選擇擬合反應時與反應分層模型的最優模型時，以偏差信息準則DIC（Spiegelhalter, Best,Carlin, & van der Linde, 2002）作為評價四個模型擬合優劣指標。DIC 值越小，說明該模型與實際數據擬合越好。

4 模擬研究

4.1 模擬設計

為了檢驗建議模型參數的估計精度，對最復雜的SAT-M3 模型進行模擬研究。各項目參數的生θi與 τi通過均值向量 0，相關 σθτ=0.5 的二元正態分布生成；最后通過反應時模型（公式1）與反應模型（公式7, M3）生成反應時與反應數據。模擬針對測驗長度（m=30, 60）以及被試量（N=500,1000）設置了2×2=4 種條件組合，每種組合重復15 次。通過計算各參數真值與估計值的MSE（mean squared error）與平均偏差（Bias）評價參數估計方法的準確性。

4.2 模擬結果

表1 是項目參數的返真性。從表中可以看出，在被試量為500，測驗長度為30 時，與其他項目參數相比，α 與a 參數估計結果偏差，MSE 值達到0.081 和0.071，而其他項目參數都低于0.05。在被試量增加到1000 時，α 與a 參數的MSE 可以達到0.06 以下，估計精度明顯提高。所有項目參數Bias 的絕對值都低于0.05，并且隨著被試量增加，Bias 絕對值普遍會有所降低。

表 1 分層模型項目參數 MSE 與 Bias

表2 為被試參數估計結果。從表2 可以看出，速度參數的MSE 值一直低于0.03，而能力參數在測驗長度從30 增加到60 時，MSE 值從0.221 減小到0.145，估計精度明顯提高；能力與速度參數的偏差Bias 都在0 上下波動，絕對值不超過0.011。

表 2 被試參數 MSE 與 Bias

從上述模擬結果可以看出，SAT-M3 分層模型的項目、被試參數通過MCMC 算法得到有效的估計，而且隨著被試量與測驗長度的增加，估計精度會相應提高。

5 實例研究

5.1 數據描述

本研究收集了被試在《瑞文標準推理測驗》上的測試數據。數據采用E-prime1.0 編寫程序收集，計時從項目出現在顯示器上開始到選擇下一個項目停止，時間的記錄單位為毫秒。被試選自兩所縣城高中的學生，測驗長度為60 個項目，控制測驗最長作答時間為40 分鐘。施測340 名被試，排除無效被試20 人，有效被試320 人。以van der Linden（2007）模型為基準模型（M0），加上本研究提出的模型共四個模型。在MCMC 估計過程中，均使用n.chain=2 條馬爾科夫鏈，且包含n.iter=30000 次迭代，燃燒次數n.burn=10000，稀疏值n.thin=2，最終剩余n.chain*（n.iter-n.burn）/n.thin=20000 次迭代用于參數估計。參數擬合收斂采用潛在量尺縮減因子（potential scale reduction factor, PSRF; Brooks & Gelman, 1998），通常PSRF＜1.1 或1.2，本研究選擇參數的PSRF 均要求小于1.2 來表示參數估計已經擬合。

5.2 研究結果

四個模型數據擬合結果如表3，SAT-M3 模型的DIC 最小，其次SAT-M1 模型，再次為SATM2 模型，最大的是M0 基準模型。根據DIC 準則，SAT-M1 與SAT-M2，都優于M0 模型；而SAT-M1 的擬合指數明顯要小于SAT-M2，說明在項目上，反應時對準確率的影響更受被試能力水平的限制。同時，SAT-M3 與SAT-M2 相比，擬合優勢并不明顯，但是三個模型都比M0 模型擬合更優，說明在考慮反應時對準確率的影響后，能明顯提高模型對數據的擬合。

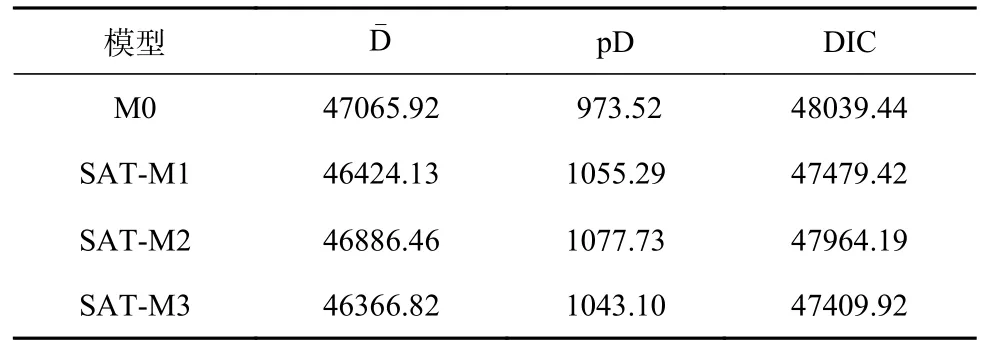
表 3 不同模型擬合指數

為了進一步分析SAT-M3 模型，了解反應時與準確率關系，繪制了殘差反應時區分度α 與難度b以及項目工作量參數β的關系（如圖2和圖3所示）。在兩圖中，水平虛線分別為b 和β 的均值，而垂直虛線固定為1。從圖2 和圖3 可以看出，α 均大于1 的項目，除了一個項目外，其它項目難度均高于均值（第一象限），此時殘差反應時與準確率關系是單調遞增（圖1-B）。在所有項目中，α 參數大于1 的項目有8 個，小于1 項目有52 個，說明在大部分項目上，被試反應時與準確率存在兩種不同類型：當能力水平低于項目難度時，被試的反應時對準確率影響為先增后減（圖1-A），而當能力水平高于項目難度時，被試反應時與準確率關系為單調遞增的曲線（圖1-C）。

6 結論與展望

當前，反應與反應時數據的聯合分析模式得到了迅速的發展，但是傳統的分層模型并未深入考慮反應時與準確率的權衡。本文結合反應時與準確率權衡SAT 模型與分層模型，對傳統分層模型進行擴展，構建了能夠反映反應時與準確率的不同關系的SAT 分層模型。從模型擬合結果可以發現，考慮反應時對準確率不同影響關系能明顯提高模型對數據的擬合。同時，根據實際數據的參數結果，不同被試在同一項目上的殘差反應時與準確率的關系存在多種形式，并且這種形式是受到被試能力與項目難度多重影響的結果。

對三個SAT 分層模型，SAT-M2 模型可能由于僅考慮了速度的影響，擬合最差。在項目作答過程中，被試速度水平即使低于項目工作量參數，但是被試只要愿意花費足夠反應時，可以彌補速度水平的不足，因此SAT-M2 與M0 在數據擬合上是趨近的，這也意味著測驗時間基本充足。而在SAT-M1 和SAT-M3 上，被試能力水平的不足是無法通過增加反應時來彌補的，而且被試在作答過程中，一個符合邏輯的心理決策過程是高難度項目放棄或者快速作答，其觀測反應時可能遠低于期望反應時，必然會降低項目作答準確率；而對于簡單項目，被試能力充足，在排除無關干擾下（失誤等因素），作答反應時是否充足是影響準確率高低的唯一因素；最后對中等難度項目，被試更愿意消耗更多反應時，甚至遠超期望反應時以提高準確率，但是受到能力水平影響，準確率增加到一定程度后，反而會降低，這種做題策略和心理與Wang 和Zhang（2006）的研究結果相一致，卻是 van der Linden（2007）分層模型所忽視的。

當然有一些問題仍然有待進一步解決與完善。在SAT 分層模型中，本研究選擇的反應時模型是對數正態反應時模型，后續研究也可以比較對數偏正態模型（孟祥斌, 2016）以及其他的認知反應時模型（Anders, Alario, & van Maanen, 2016;Heathcote, 2004）的實際擬合結果。同時，在SAT 分層模型中，反應時與準確率在認知能力測驗項目上存在非單調關系，造成的原因除了項目難度以及能力等因素外，也可能與被試認知風格、人格等因素相關（Grigorenko & Sternberg, 1995;Kagan, Rosman, Day, Albert, & Phillips, 1964）。