模態參數識別和輸入整形相結合的抑振方法*
李 琳, 胡錫欽, 鄒焱飚
(華南理工大學機械與汽車工程學院 廣州,510641)
引 言
自動化技術的發展促使工業機器人被廣泛應用在生產制造領域,隨著生產要求的提高,實現機器人高速高精度的運動變得尤為重要。然而,高速運動會使機械臂產生較大的殘余振動,實際生產中,通常需要等到殘余振動消失或者衰減到允許范圍之后才能進行位置精度要求高的工序,這就很難滿足生產的要求。為了消除這種振動帶來的副作用,提高工作效率,研究人員進行了大量的研究工作。近年來,輸入整形技術成為振動控制領域的研究熱點。文獻[1-3]對輸入整形技術進行了深入的研究,分析了整形器的魯棒性以及對模態參數的敏感性,并在不同應用實例中驗證了其有效性。董明曉等[4-5]針對彈性機構中的單模態和多模態振動問題,提出將輸入整形引入到比例-微分(proportion derivative,簡稱PD)反饋控制中,通過合理的設計控制器,使其具有較強的參數魯棒性和抗外界干擾能力。趙志剛等[6]提出了改進型負輸入整形和最優控制結合的方法,引入線性二次型調節器反饋以應對模型參數不精確的問題。賈鵬霄等[7]將PD自適應控制與輸入整形技術相結合,考慮系統模型存在參數不匹配的影響,利用輸出信息進行PD自適應控制器的設計,保證跟蹤參考模型的輸出以獲得滿意的性能。然而,這些方法都是以簡化、理想化的動力學模型為基礎,這使得獲取到的模態參數與實際系統的模態參數不匹配。
鑒于在設計輸入整形器時,整形器脈沖序列中各脈沖的幅值和作用時刻的求解要求精確的動力學模型,且對模型參數的變化很敏感,而采用魯棒輸入整形器雖然擴大了帶寬,但卻要消耗大量的調節時間。為此,既考慮到輸入整形器對系統振動模態參數的敏感度很高,也考慮到輸入整形器會帶來延時,影響機器人的工作效率,筆者提出一種基于模態參數識別和無延時整形相結合的復合方法來抑制機械臂的殘余振動。
1 輸入整形原理
輸入整形是將初始指令與特定的脈沖序列進行卷積,生成的整形指令作為控制系統運動的輸入信號[6]。其基本原理可以由圖1來描述,在t1=0時刻輸入幅值為A1的脈沖信號,系統響應在圖中用實線表示,為了抑制由第1個脈沖激起的振動,在t2=ΔT時刻輸入幅值為A2的脈沖信號,其響應在圖中用虛線表示。由線性系統的疊加性可知,兩個脈沖引起的系統響應如圖中點畫線所示,當t≥ΔT時,兩個脈沖激起的振動相互抵消,達到抑振的目的。
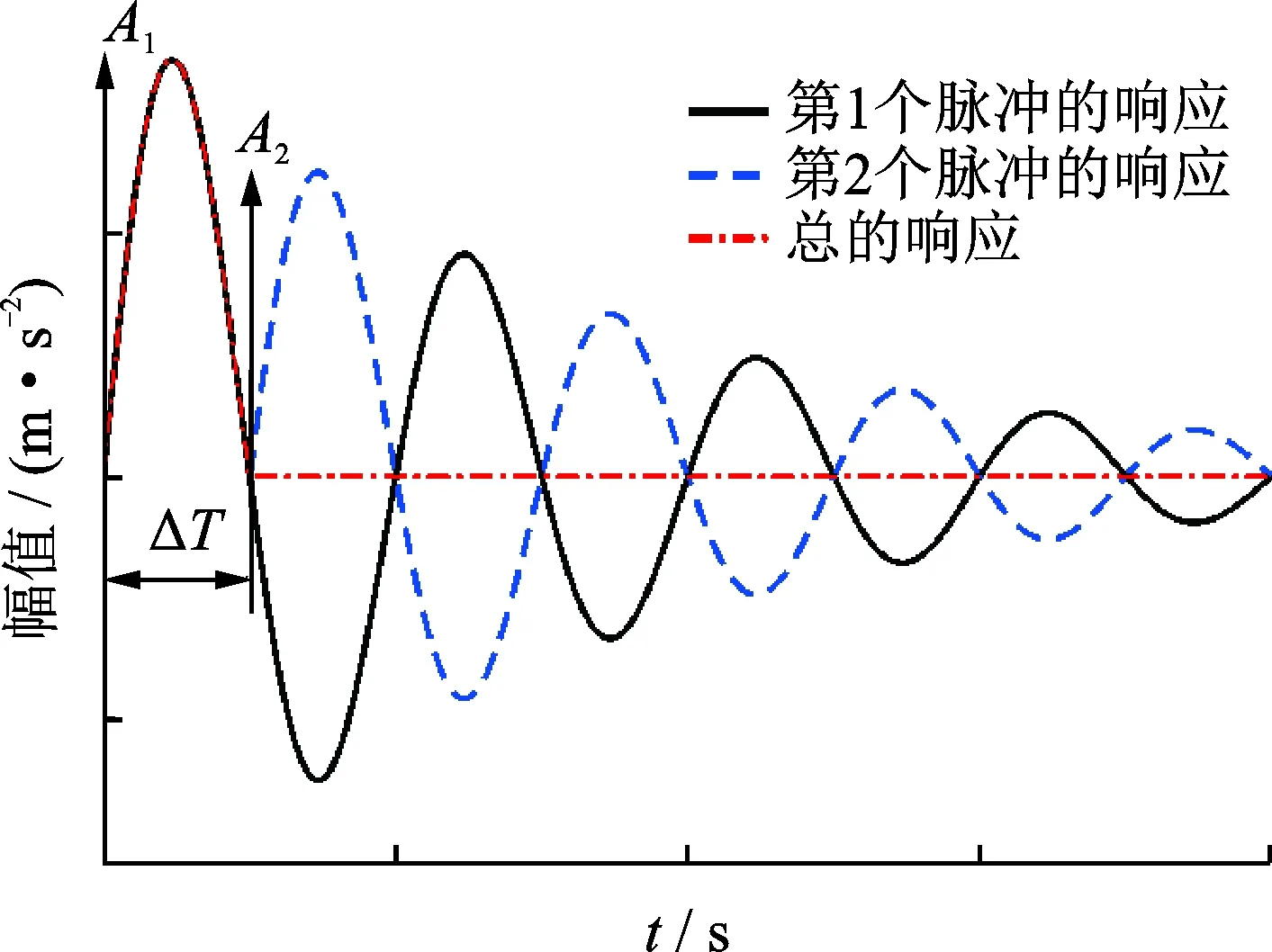
圖1 輸入整形法原理Fig.1 Principle of input shaping
下面通過二階線性系統來引出輸入整形器的設計過程,假設二階線性系統的傳遞函數為G
(1)
其中:ωn為自然頻率;ζ為阻尼比;k為增益。
二階線性系統的單位脈沖響應為
(2)
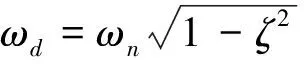
假設整形器由n個脈沖組成,那么整形器可表示為
(3)
以包含n個脈沖的脈沖序列作為系統的輸入信號,則系統響應為
V2cos(ωd(t-ti))]
(4)
(5)
(6)
其中:Ai,ti分別為第i個脈沖的幅值和作用時刻;tn為輸入整形器的總長度。
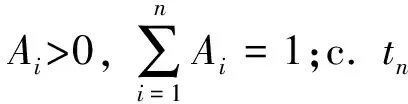
對于某一確定的系統,其自然頻率ωn、阻尼系數ζ是確定的,根據上述約束條件可以解出Ai和ti
(7)
其中
最簡單的輸入整形器是包含兩脈沖的整形器,稱之為ZV整形器,由式(7)可得其數學表示形式為
(8)

2 模態參數的識別
整形器的設計需要預先獲知系統的兩個模態參數:自然頻率ωn和阻尼比ζ。傳統的方法主要有3種:a.建立系統的動力學模型,通過求解動力學方程來獲得[8-9];b.通過錘擊法等進行模態實驗獲得[10];c.有限元分析法[11]。這3種方法都能得到系統的各階模態,但不能直接確定在實際情況下起主要作用的模態,通常的做法是取第1階模態或者前2階模態來設計整形器。
筆者通過對機械臂末端的殘余振動信號進行快速傅里葉變換(fast fourier transform,簡稱FFT),分析其主要模態,來識別系統的模態參數[12]。具體步驟如下:
1) 對采集到的殘余振動信號進行FFT計算,繪制殘余振動信號的功率譜;
2) 設定頻譜幅度比較閾值Av和頻率變化閾值ωv,篩選幅值大于Av的峰值頻率ωi,再比較相鄰的峰值頻率ωi,若ωi+1-ωi<ωv,則當成同一階模態頻率,如此確定在系統振動中起主要作用的模態;
3) 根據步驟2中識別到的主振頻率ωi,設置帶通濾波器,對殘余振動信號進行濾波,得到該模態下的振動時域信號;
4) 通過對數衰減法求解阻尼比[13]。
對數衰減法的計算原理如圖2所示。
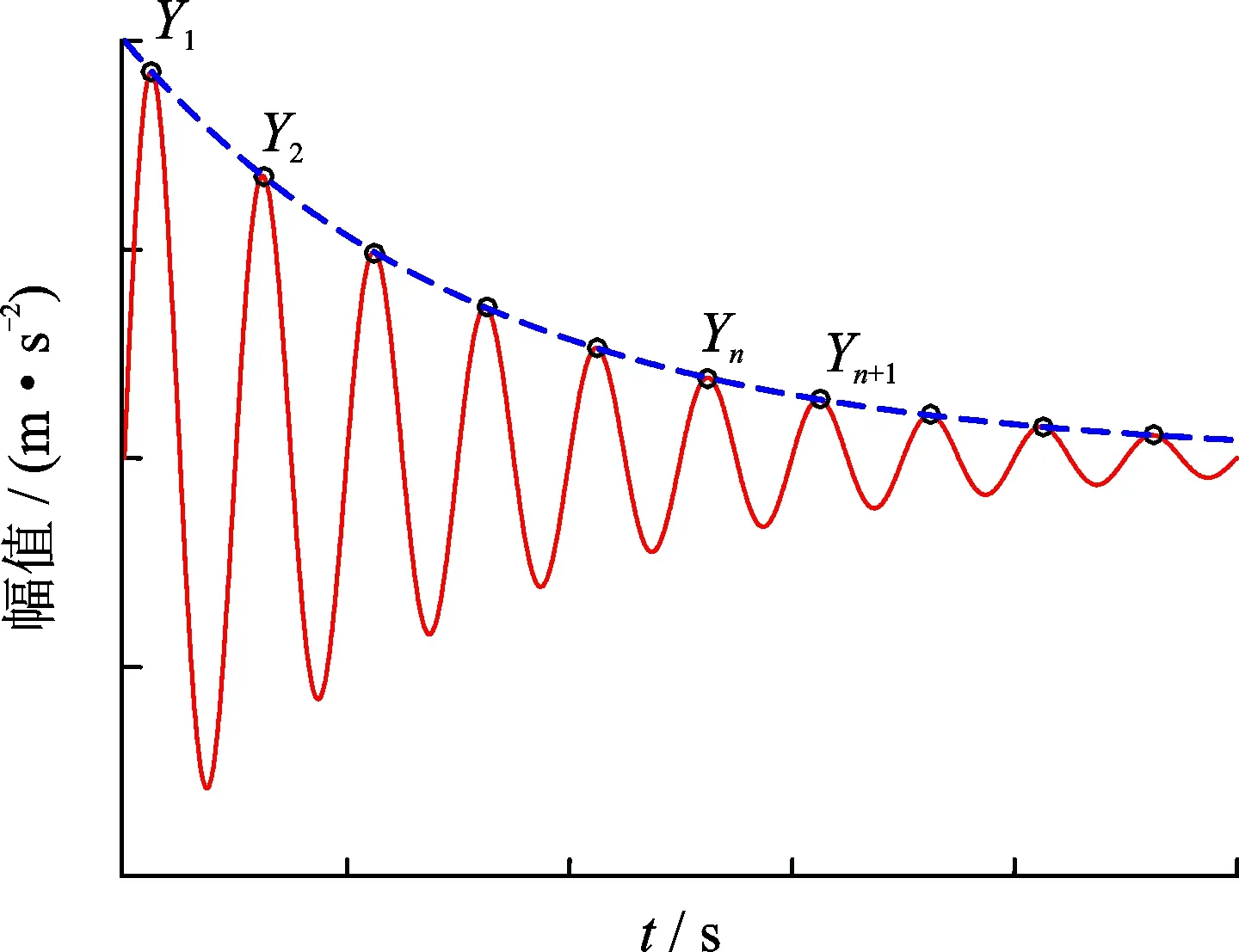
圖2 對數衰減法原理Fig.2 Principle of logarithmic decrement method
由式(2)可知,第i階模態下的振動信號為
(9)
其中:i為主振模態序號;N為主振模態的數量。
由式(9)可知,振動信號為衰減的正弦信號,其包絡線為
(10)
設振動信號中兩個連續的峰值為Yn和Yn+1,那么
為提高計算的準確率,可以選擇多個峰值計算出阻尼比ζ之后再取平均值。
3 無延時整形的設計方法
傳統的輸入整形器會引入延時,如果采用魯棒性強的整形器,就不得不增加整形器中脈沖的數量,這將使延時更加嚴重。為了消除延時帶來的副作用,筆者采用一種對輸入軌跡進行加速設計實現無延時的方法,具體設計思路如下。
1) 典型的整形器可表示為
其中:n為脈沖數;tn為整形器的長度,對輸入軌跡整形后會使得軌跡時長增加tn。
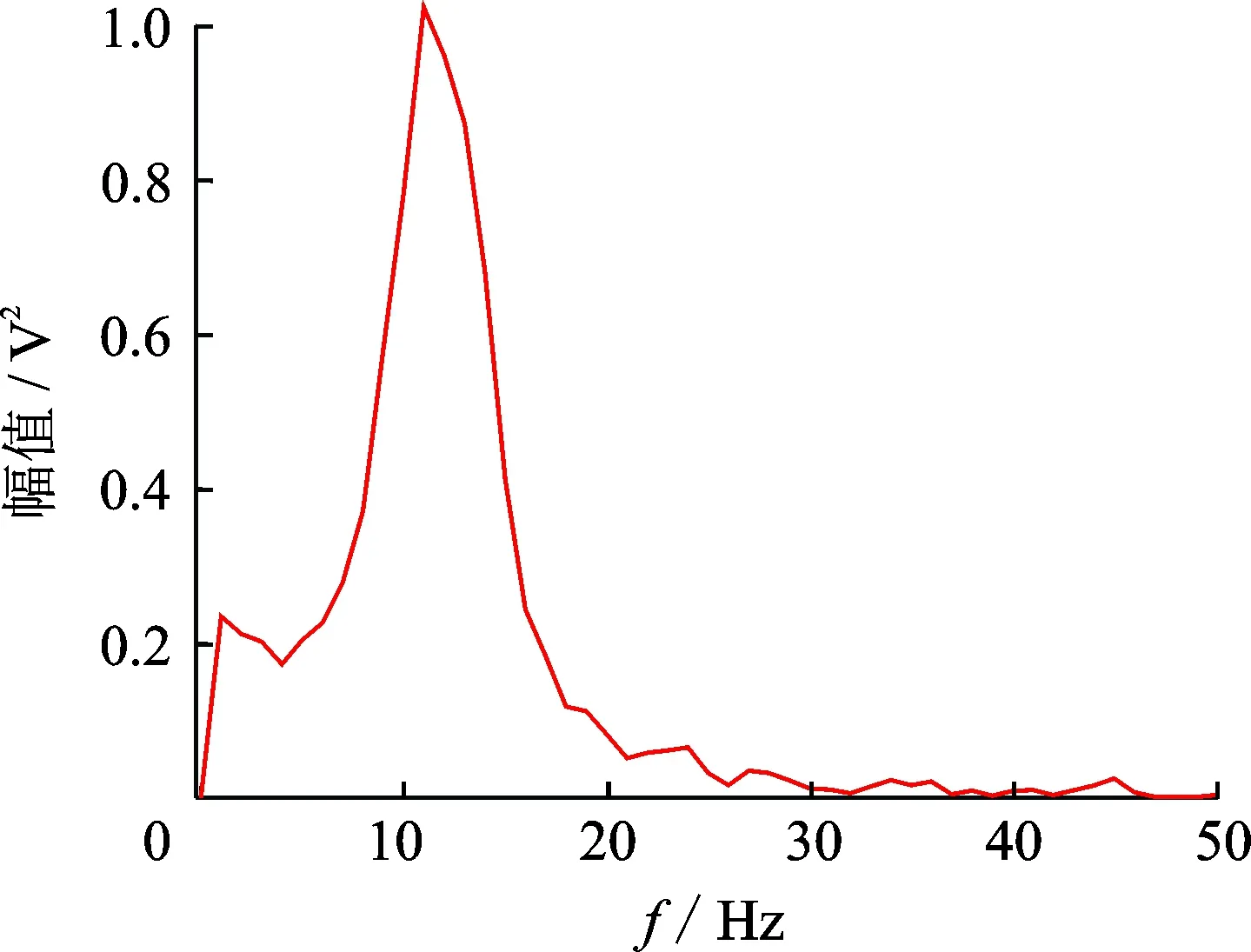
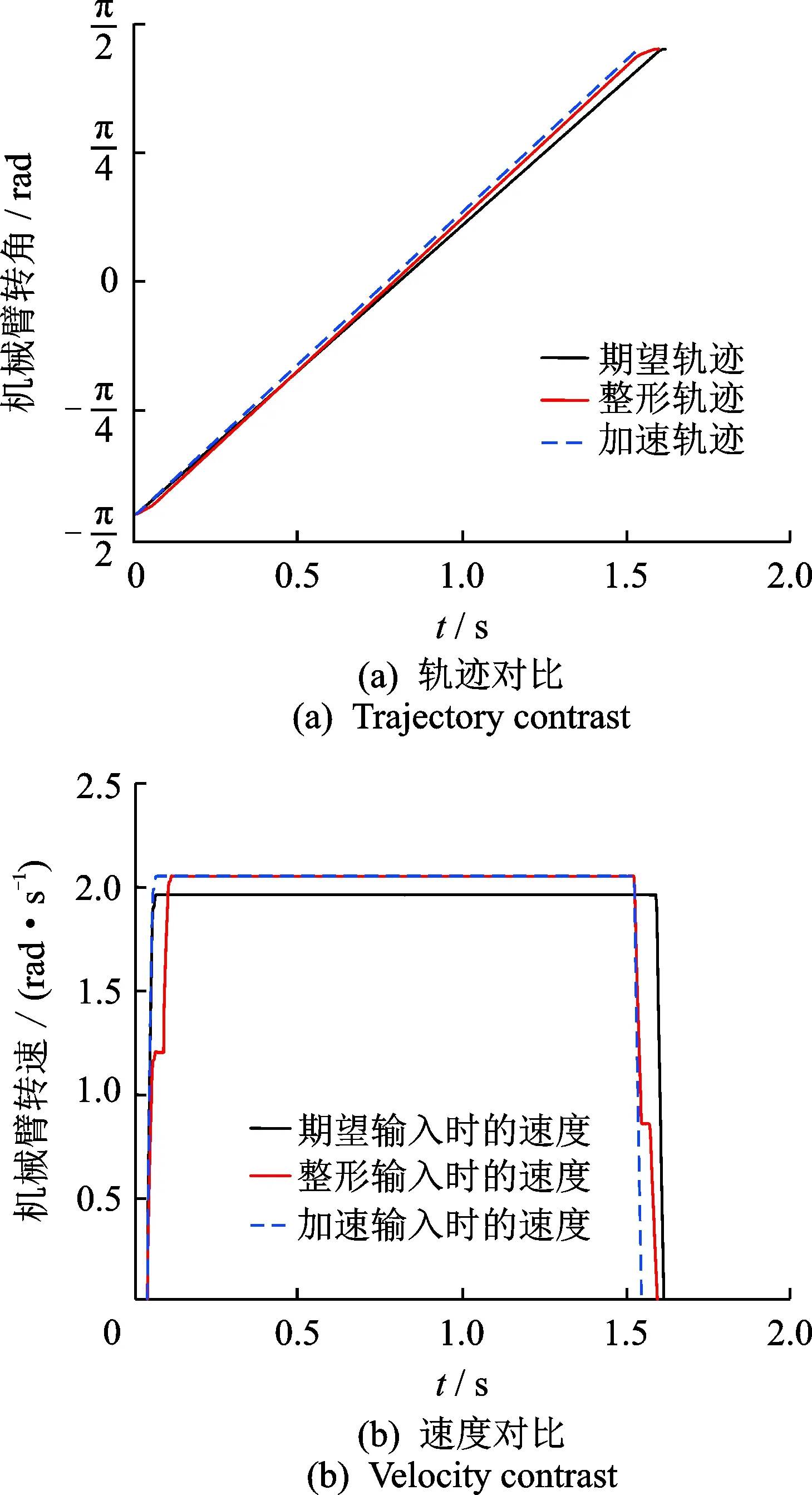
2) 對期望的輸入軌跡S(t)(t∈[0,T])進行加速設計得到Sacc(τ)(τ∈[0,T-tacc]),即按時間變量對軌跡均勻加速,使軌跡時長縮短tacc。其中tn≤tacc 則Sacc(τ)=Sacc(kt)=S(t),t∈[0,T]。如此,確保加速設計后的軌跡與原軌跡保持形狀不變,即軌跡曲線的各階導數的連續性特性不變,而只改變運行速度。 3) 對加速后的軌跡Sacc(τ)進行整形,得到整形后的軌跡SIS=fIS*Sacc。假設整形器包含n個脈沖,則整形后的軌跡為 (t∈[0,T-tacc+tn]) S'acc(t)是對Sacc(t)的擴展,即 其中:u(t)為單位階躍函數 其目的是確保整形后機械臂能運行到與未整形時同樣的位置,即機械臂運動的起止點相同。 比較原期望的軌跡s(t),t∈[0,T]與整形后的加速軌跡SIS(t),t∈[0,T-tacc+tn]可知,由于tn 為了驗證上述方法的有效性,搭建了單自由度機械臂的實驗平臺,并進行了間歇-間歇實驗來測試抑振效果。 實驗平臺如圖3所示,機械臂實體采用廣州數控設備有限公司生產的六自由度工業機器人的J4和J5軸,其中J4軸固定在基座上,J5軸由交流伺服電機通過同步帶驅動。驅動模塊采用臺達公司的ASD-A2 Ether-CAT通訊型交流伺服驅動器和ECMA-CA0604SS型交流伺服電機,電機額定功率為400W,額定轉速為3kr/min。傳感器采用的是德國KISTLER公司的三維加速度傳感器,測量范圍為-300 ~ +300m/s2。信號處理模塊為華研 IPC-510嵌入式工控機,配置主頻3.4GHz的Intel i7-3770四核處理器。實驗中輸入控制信號為機械臂的位移軌跡,輸入指令間隔為1ms,模態參數識別的計算過程在Matlab中完成。 圖3 抑振測試實驗平臺Fig.3 Experiment platform for vibration suppression control 本實驗中輸入軌跡為典型的S型曲線,機械臂按照規劃的軌跡運行,通過加速度傳感器采集機械臂末端殘余振動的電壓信號,將原始振動信號進行低通濾波,濾除高頻噪聲,再進行快速傅里葉變換得到的功率譜如圖4所示。 圖4 振動信號功率譜Fig.4 Power spectrum of residual vibration 根據前述參數識別法,本實驗中系統的主振頻率為11Hz,此處分別用波峰值和波谷值進行對數衰減法求解阻尼比,再取平均值以提高準確性,結果為ζ=0.11。 根據4.1節中所得模態參數設計輸入整形器,由式(8)可知ZV整形器的數學表達式為 根據前述無延時設計的方法,對原始期望軌跡進行整形,結果如圖5所示。由圖5(a)可知,加速設計后的軌跡與原期望軌跡形狀相同而時長縮短,整形軌跡較貼合期望軌跡。由圖5(b)可知,整形后實際的運行時間為1.6s,而預先期望軌跡的運行時間為1.62s,這說明通過對軌跡加速設計可以實現無延時的目的。 圖5 無延時設計Fig.5 Zero time delay method 首先令機械臂按照期望的軌跡運行,通過加速度傳感器采集末端的殘余振動信號,如圖6(a)所示。起始時間為期望軌跡運行完的時刻,總時長為1s。 圖6 抑振效果Fig.6 Effect of vibration suppression 設整形前后殘余振動信號分別為y1(t)和y2(t)。為方便討論,此處將振動數據按整形前殘余振動的最大幅值max(|y1(t)|)做歸一化處理(量綱為1) 其中:max(|y1(t)|)=12.7m/s2。 考慮到噪音以及加速度傳感器可能存在的信號波動的影響,設定|y1*(t)|≤0.2時(圖中用虛線標出),認為振動已經穩定下來,則整形前系統的穩定時間為0.118s。 圖6(b)所示為機械臂按無延時整形軌跡運行時,從加速度傳感器采集到的振動信號y2*(t)。起始時間為機械臂運動停止時刻,總時長為1s。此處仍按整形前振動的最大幅值max(|y1(t)|)做歸一化處理(量綱為1) 整形后系統殘余振動的最大幅值僅為整形前的31%,穩定時間為0.043 s。 對比整形前后機械臂的運行時間和穩定時間,如表1所示。其中總時間為運行時間(即軌跡時長)與穩定時間之和,殘余振動的穩定時間由整形前的0.118 s縮短到整形后的0.043 s,穩定時間大大縮短,說明輸入整形器設計合理,抑振效果非常理想。 表1 實驗結果對比 利用輸入整形技術抑制機械系統的殘余振動時,通常難以獲取系統的模態參數,致使參數不匹配,從而影響抑振效果。同時,輸入整形器不可避免地給系統帶來延時,影響工作效率。筆者提出了一種基于模態參數識別和無延時輸入整形相結合的復合方法來抑制機械臂的殘余振動,并且在單自由度機械臂系統上進行實驗以驗證其有效性。實驗結果顯示,整形后機械臂末端殘余振動的最大振幅降低到整形前的31%,穩定時間由整形前的0.118 s縮短到整形后的0.043 s,表明通過該方法識別到的振動模態參數準確性較高,設計的輸入整形器合理。同時,機械臂的運行時間由1.62 s降低為1.6 s,說明無延時設計方法有效地補償了輸入整形器所帶來的延時,運動控制的總時間由整形前的1.738 s降低到1.643 s,保證了機器人的工作效率。
4 實 驗

4.1 模態參數識別
4.2 整形器設計
4.3 抑振效果


5 結束語

