子結構法在齒輪-箱體-基座耦合系統輻射噪聲仿真中的應用研究

王晉鵬，宋 敏，王 鵬，劉 嵐，王 瑩

(1.西安航空學院 機械工程學院，西安710077；2.西北工業大學 陜西省機電傳動與控制工程實驗室，西安710072)

齒輪傳動由于具有傳動比精確、效率高、工作可靠、壽命長等優點已成為工業領域中最常用的傳動形式之一。齒輪傳動裝置在工作過程中由于嚙合剛度波動、制造和安裝誤差等內部激勵的影響會產生振動并輻射噪聲，不僅影響工作環境的舒適性，甚至會對工作人員的身體造成危害。如何快速準確低預估齒輪傳動裝置的輻射噪聲是實現對其有效控制的基礎，有著重要意義。

齒輪傳動裝置的輻射噪聲主要由以下3 部分組成：

（1）齒輪、軸等的噪聲穿透箱體產生的空氣噪聲；

（2）軸端部振動產生的輻射噪聲；

（3）箱體振動產生的輻射噪聲[1]。

由于箱體的隔聲作用，第三部分是齒輪傳動裝置輻射噪聲的主要來源，目前對于齒輪傳動裝置的輻射噪聲分析就是對該部分進行分析。通過建立并求解齒輪系統的動力學方程獲得軸承動載荷，以軸承動載荷為激勵采用有限元/邊界元法對箱體的輻射噪聲進行分析是目前齒輪傳動裝置輻射噪聲分析中常用的方法之一，其準確性已經得到了廣泛驗證[2-3]。

齒輪傳動裝置通常安裝在基座上，在齒輪箱傳動裝置的輻射噪聲分析中必須計入基座的影響。通過建立基座的有限元/邊界元模型可計入其影響，但該方法同時也會增加計算規模，降低計算效率。如何提升齒輪-箱體-基座耦合系統輻射噪聲的分析效率是目前需要解決的問題之一。

子結構法是提升計算效率的常用方法之一，其在機械結構的振動分析中已經得到了廣泛應用。柴國棟[4]、王雪仁[5]、陳冬冬[6]和張忠[7]等分別應用該方法對電子設備、圓柱殼體、鋁合金車體和運載火箭的固有特性進行了分析。但該方法在輻射噪聲分析中的應用還較少。

本文以一個安裝在基座上的齒輪傳動裝置為對象，采用靜態子結構法對基座進行了等效，在此基礎上建立了輻射噪聲分析模型，通過求解獲得了齒輪-箱體-基座耦合系統在不同場點上的聲壓級頻譜，并與全有限元/邊界元模型的分析結果進行了對比，證明了文中方法的準確性和有效性。

1 模型建立

在已知齒輪系統參數（包括齒輪參數、軸的尺寸、軸承型號等）、箱體和基座結構的條件下，可根據以下流程建立齒輪-箱體-基座耦合系統輻射噪聲分析模型。

首先根據齒輪參數建立齒輪系統的動力學方程，求解該方程可獲得各軸承在不同方向上的動載荷。接著將箱體離散成有限個單元，在每個軸承孔的中心處建立中心節點，并在各中心節點與對應軸承孔內壁所有節點之間建立剛性耦合，將軸承動載荷施加在對應軸承孔的中心節點處，可建立齒輪-箱體耦合系統的運動學方程，如式(1)所示。

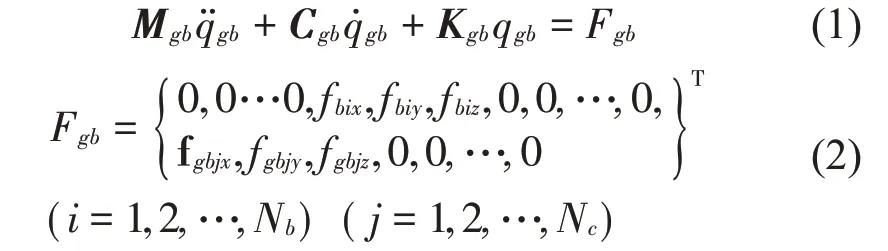
式中：Mgb，Cgb和Kgb分別表示箱體的質量、阻尼和剛度矩陣；qgb表示位移向量；Fgb表示載荷向量；fbix，fbiy和fbiz表示第i個軸承處x，y和z方向上的載荷；Nb表示軸承個數；fgbjx，fgbjy和fgbjz表示第j個連接點處x，y和z方向上基座對箱體的載荷；Nc表示連接點數。

然后，將基座離散成有限個單元，并將基座與箱體的各連接點設置為主節點（外部節點），將其它節點設置為內部節點。此時基座剛度矩陣以及相應的節點位移和載荷向量可以寫成如式(3)所示的分塊形式。

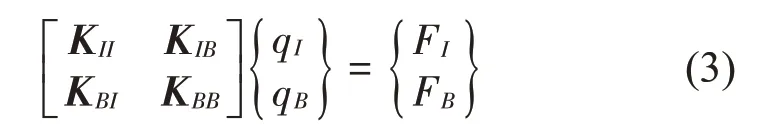
式中，下標I代表內部節點自由度，下標B代表外部節點自由度。

式(3)的展開形式如式(4)和式(5)所示。

根據式(4)可以得到內部節點的位移，如式(6)所示。

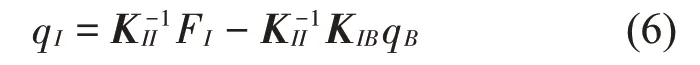
將式(6)帶入式(5)可以得到凝聚后的基座的運動方程，如(7)所示。

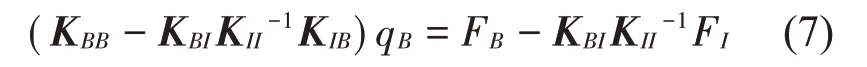
式(7)的簡化形式如式(8)所示。

式中：K*BB和F*B就是經凝聚后基座的剛度矩陣和載荷向量。同理可得到經凝聚后基座的質量矩陣M*BB。可以看出K*BB(M*BB)綜合了原始剛度（質量）矩陣中各分塊矩陣的影響。

矩陣M*BB中非對角線元素（耦合項）對振動噪聲的影響要明顯小于對角線元素（非耦合項）。因此可以忽略該矩陣中的非對角線元素，得到基座的等效質量矩陣，如式(9)所示

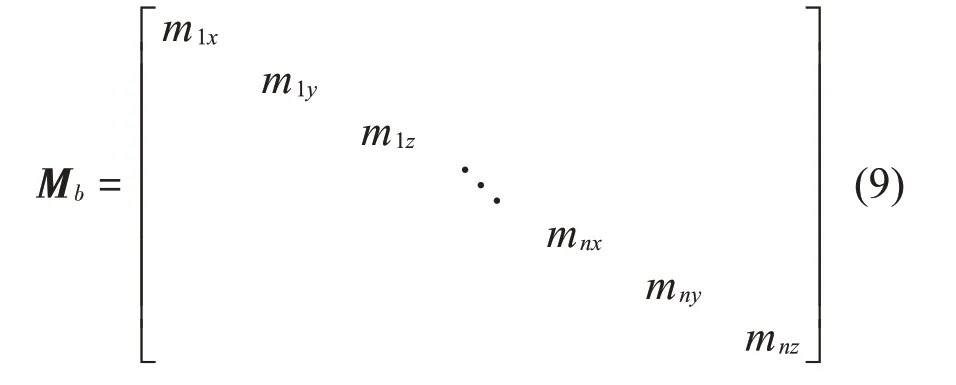
式中：mjx、mjy、mjz(j=1,2,…,Nc)表示凝聚后基座在各連接點處不同方向上的等效質量。

同理可得到基座的等效剛度矩陣，如式(10)所示

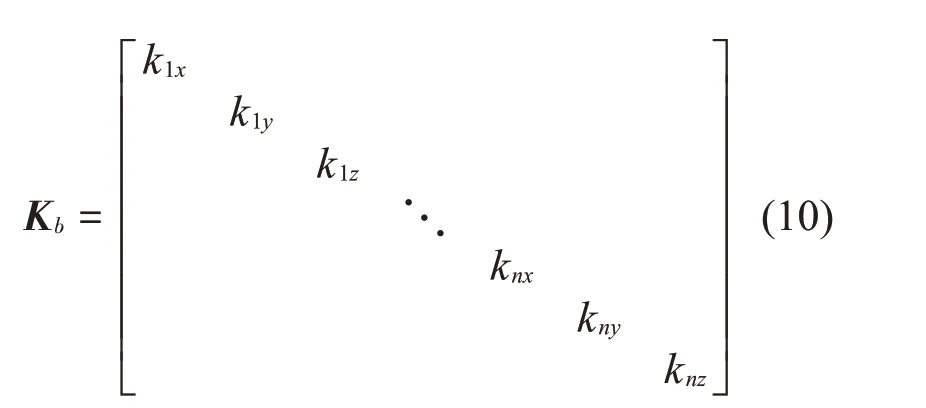
式中：kjx、kjy、kjz(j=1,2,…,Nc)表示基座在各連接點處不同方向上的等效剛度。

在獲得了基座的等效質量矩陣和等效剛度矩陣后，可建立其運動學方程，如式(11)所示。

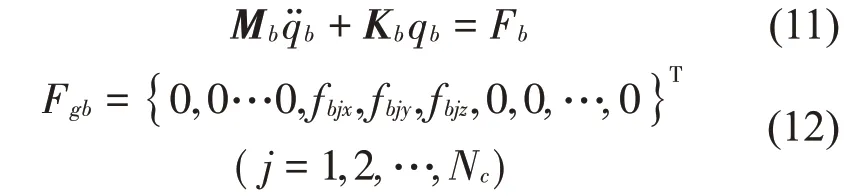
式中：qb表示基座的位移向量；fbjx，fbjy和fbjz表示第j個連接點處x，y和z方向上箱體對基座的載荷。

每個連接點處，箱體與基座的位移相等；載荷大小相等，方向相反。根據該邊界條件對箱體和基座的質量矩陣、阻尼矩陣以及剛度矩陣進行組裝可建立齒輪-箱體-基座耦合系統的運動學方程，如式(13)所示。（注：文中未考慮基座的阻尼特性，即基座等效阻尼矩陣中的各元素均為0）。

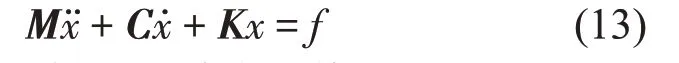
式中：M、C、K分別為耦合系統的整體質量、阻尼和剛度矩陣分別為耦合系統的加速度，速度和位移向量；f為載荷向量。

采用模態疊加法對方程(13)進行求解可以得到箱體表面各節點的法向振動速度，如式(14)所示。

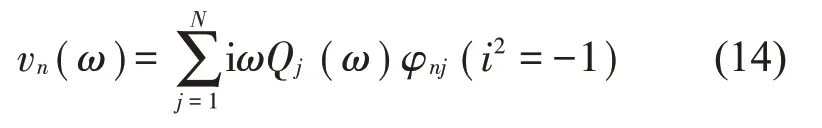
式中：vn表示箱體表面的法向速度；ω表示角頻率；j表示模態階數；N表示模態總階數；Qj(ω)為結構模態參與因子，代表了各階模態在結構振動響應中的重要程度；φnj表示箱體的第j階主振型在各表面上的法向分量。

高階模態對結果振動的貢獻非常小，因此為了在計算精度和計算規模之間更好地達到平衡，一般只取系統的前l階模態進行求解。

箱體一般具有較大的結構剛度，聲壓變化對結構振動的影響非常小，可忽略不計，其在空氣中的穩態聲學響應可用Helmholtz 方程表示[8]，如式(15)所示。

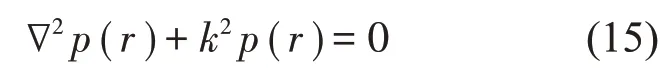
式中：?為拉格朗日算子；p(r)表示聲場中任意位置r處的聲壓；k為波數。

采用間接邊界元法對式(15)求解可以得到聲場中任意場點在不同頻率下的聲壓如式(16)所示。

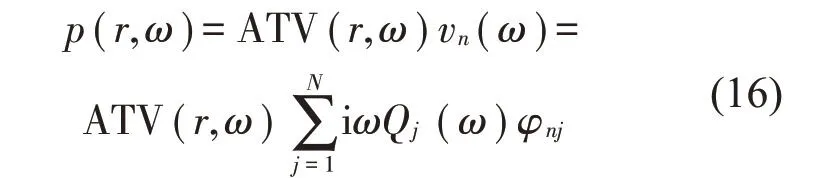
式中：ATV(r，ω)為聲學傳遞向量，代表了聲場中任意場點處的聲壓與箱體表面法向振動速度間的關系。

2 結果與討論

2.1 分析對象

采用上述模型，對一個剛性安裝在基座上的齒輪傳動裝置的輻射噪聲進行了仿真分析。齒輪傳動系統的簡圖如圖1所示。

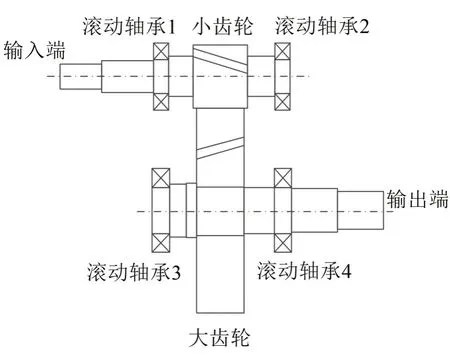
圖1 齒輪系統簡圖

可以看出傳動系統中的齒輪副為斜齒輪副，其參數如表1所示。箱體的實體模型如圖2(a)所示，為了方便計算，在建模時忽略了箱體上一些細小的結構特征，如小的倒角，小的螺栓孔等。基座的實體模型如圖2(b)所示。箱體與基座通過6個螺栓相連，對應的連接點編號如圖2(b)所示。

表1 斜齒輪副的基本參數

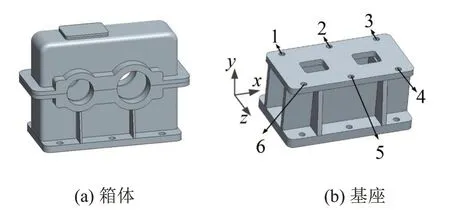
圖2 箱體和基座的實體模型

2.2 軸承動載荷

將圖1所示的齒輪系統離散成一系列節點并組成不同類型單元，建立了其有限單元模型[9]，如圖3所示。從圖3中可以看出，齒輪系統的有限單元模型中共包含4 類節點和3 類單元。其中軸節點通常選取在軸的端點、軸截面尺寸有突變處、軸承寬度端點處以及齒輪齒寬端點處。功率節點通常選取在功率輸入端（輸出端）平鍵、花鍵或聯軸器的中點處。軸承節點通常選取在軸承中點處。齒輪節點通常選取在齒寬中點處。軸單元建立在同一根軸上的相鄰節點之間，文中用Timoshenko 梁單元來模擬軸單元。嚙合單元建立在兩嚙合齒輪節點之間，文中在建立嚙合單元時忽略了兩嚙合齒輪間的相互摩擦。軸承單元建立在軸承節點和固定點之間，文中通過滾動軸承在各方向上的剛度和阻尼來等效軸承單元。

圖3 齒輪系統的有限單元模型

通過求解齒輪系統的有限單元模型，獲得了各軸承節點在不同方向上的位移和速度，將該位移和速度與對應的軸承剛度和阻尼相乘并求和獲得了各軸承在不同方向上的動載荷。輸入轉速為3 000 r/min，輸出扭矩為2 000 N·m 時各軸承在不同方向上的動載荷如圖4所示。從圖4中可以看出，各軸承上動載荷的峰值主要出現在嚙合頻率（1 450 Hz）及其二倍頻（2 900 Hz）處。輸入軸各軸承（軸承1和軸承2）上的動載荷明顯大于輸出軸各軸承（軸承3 和軸承4），主要因為輸入軸的剛度小于輸出軸，在相同工作條件下，輸入軸的振動比輸入軸明顯。

2.3 基座的等效質量和剛度

由箱體振動產生的輻射噪聲是齒輪傳動裝置輻射噪聲的主要來源，因此為了提升計算效率對基座進行了等效。建立基座的有限元模型并在各連接點處設置主節點，通過子結構法獲得了基座在各連接點處不同方向上的等效質量，結果如表2所示。由于基礎結構的對稱性，連接點1、3、4和6處的等效質量基本相同，連接點2和5處的等效質量基本相同。

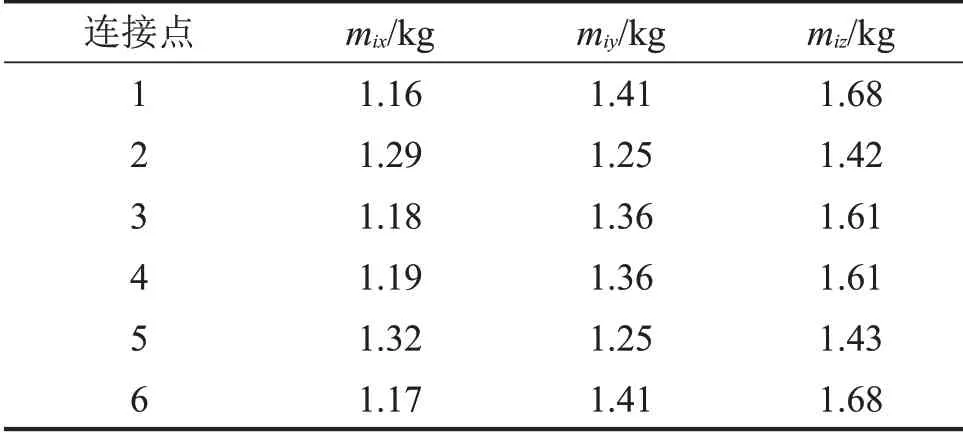
表2 基座在各連接點處的等效質量

建立基座的有限元模型，分別在各連接處的不同方向上施加單位載荷，通過靜力學分析獲得了各連接點處不同方向上的位移，用載荷除以對應的位移獲得了基座在各連接點處不同方向上的等效剛度，結果如表3所示。

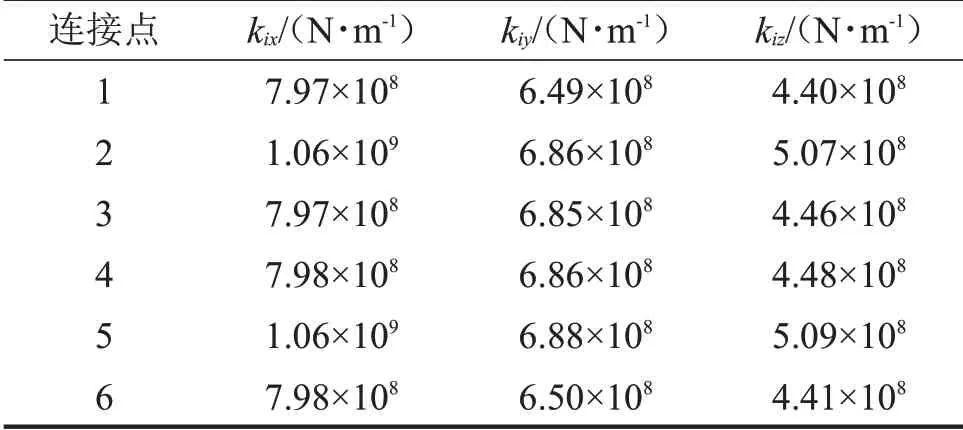
表3 基座在各連接點處的等效剛度

可以看出連接點1、3、4 和6 處的等效剛度基本相同，連接點2 和5 處的等效剛度基本相同，產生該現象的主要原因是基座結構的對稱性。

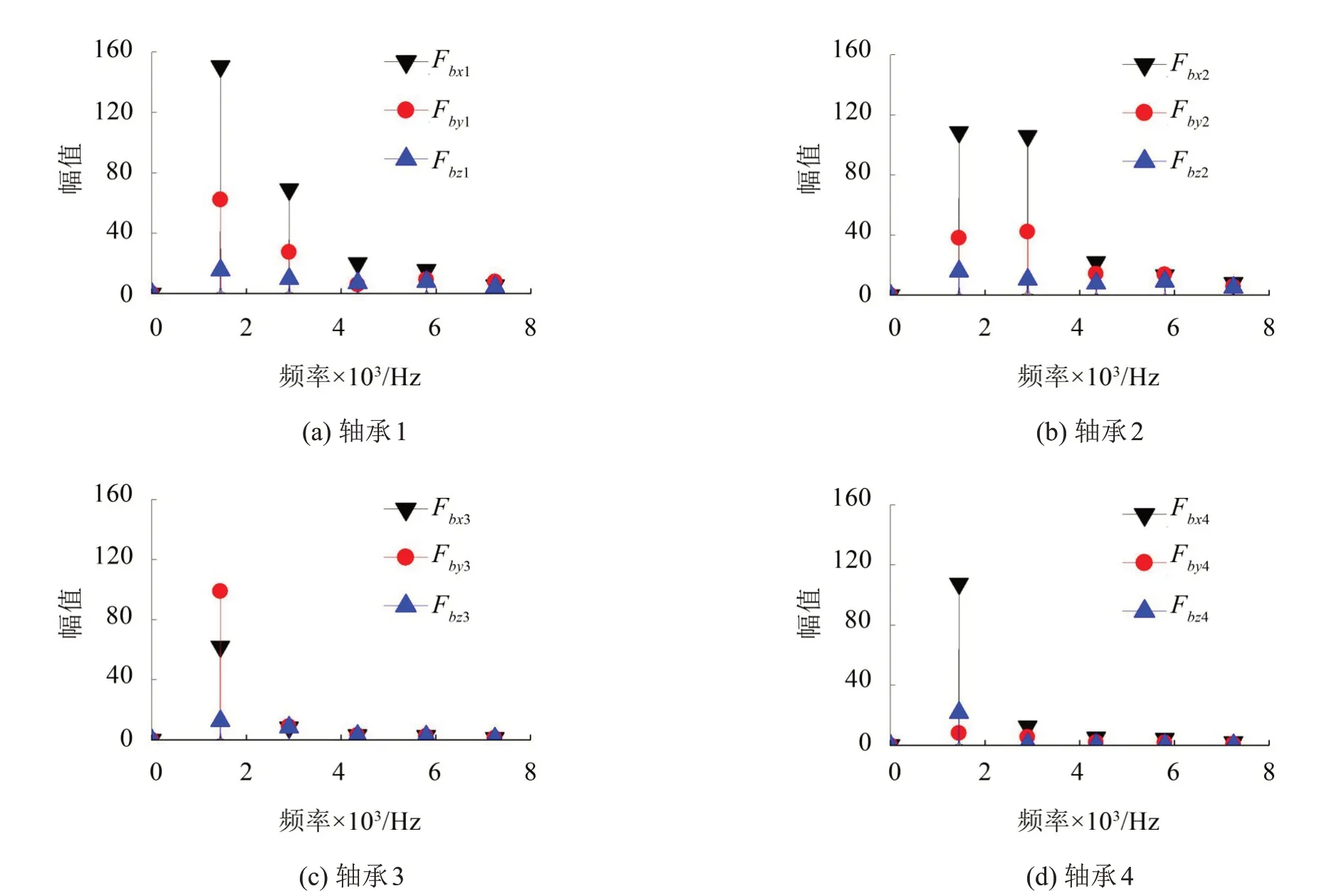
圖4 各軸承上的動載荷頻譜

2.4 輻射噪聲

將箱體離散成有限個單元，并在各連接點處以質量單元和彈簧單元等效基座，以各軸承上的動載荷作為激勵采用有限元/邊界元法分析獲得了各場點上的輻射噪聲。輸入轉速為3 000 r/min，輸出扭矩為2 000 N·m 時各場點（場點位置如圖5所示）上的聲壓級頻譜如圖6所示。從圖6中可以看出各場點上聲壓級的峰值均出現在嚙合頻率（1 450 Hz）及其2 倍頻（2 900 Hz）處，與軸承動載荷的分布規律一致。

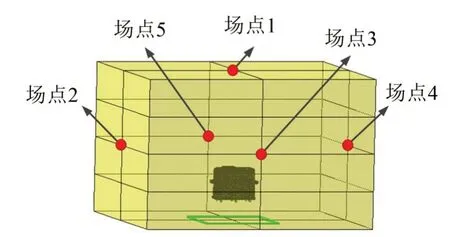
圖5 各主要場點的位置

3 模型驗證

為了驗證文中提出的基于子結構法的齒輪-箱體-基座耦合系統輻射噪聲分析模型的準確性，建立了箱體-基座的全有限元/邊界元模型（如圖7所示），在軸承孔處施加對應的軸承動載荷對齒輪-箱體-基座耦合系統的輻射噪聲重新進行了分析，并與通過子結構法獲得的分析結果進行了對比。

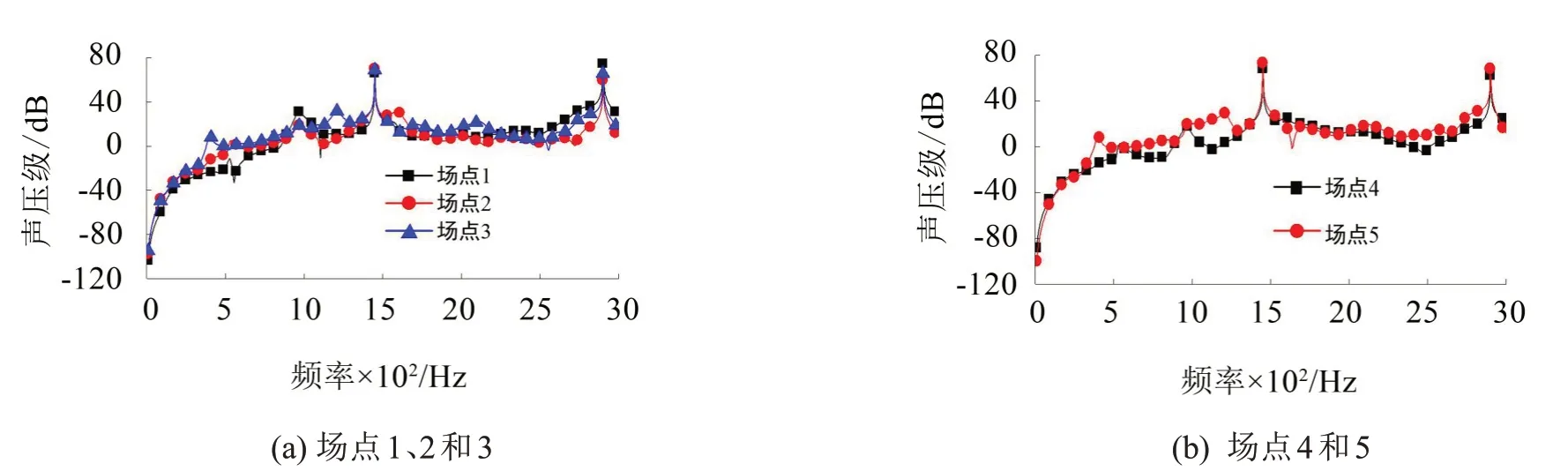
圖6 各場點上的輻射噪聲頻譜

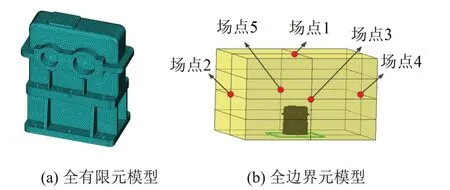
圖7 齒輪-箱體-基座的全有限元/邊界元模型

輸入轉速為3 000 r/min，輸出扭矩為2 000 N·m時通過不同方法獲得的各場點上的輻射噪聲頻譜如圖8-圖12所示。

從圖8-圖12中可以看出通過子結構法和全有限元/邊界元法分析獲得的各場點上聲壓級頻譜的峰值均出現在嚙合頻率及其2 倍頻處，并且峰值都比較接近。

表4中對比了輸入轉速為3 000 r/min，輸出扭矩為2 000 N·m時通過子結構法和全有限元/邊界元法分析獲得的各場點上的有效聲壓級。

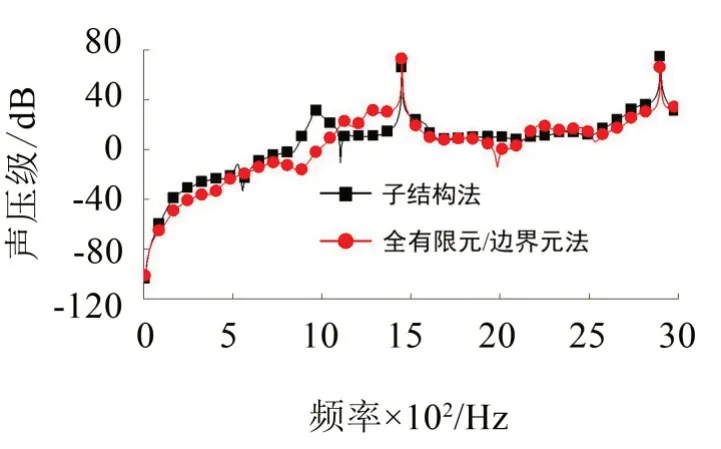
圖8 場點1上輻射噪聲頻譜對比

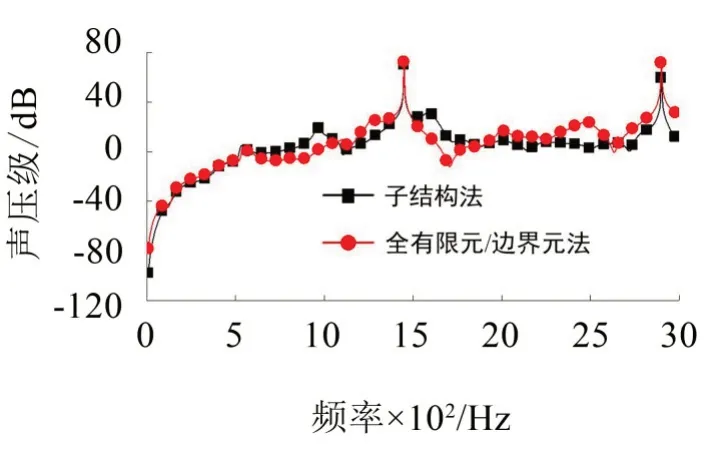
圖9 場點2上輻射噪聲頻譜對比

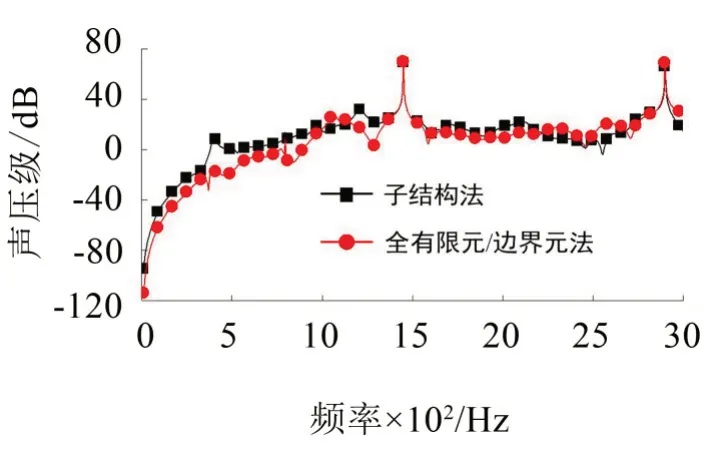
圖10 場點3上輻射噪聲頻譜對比

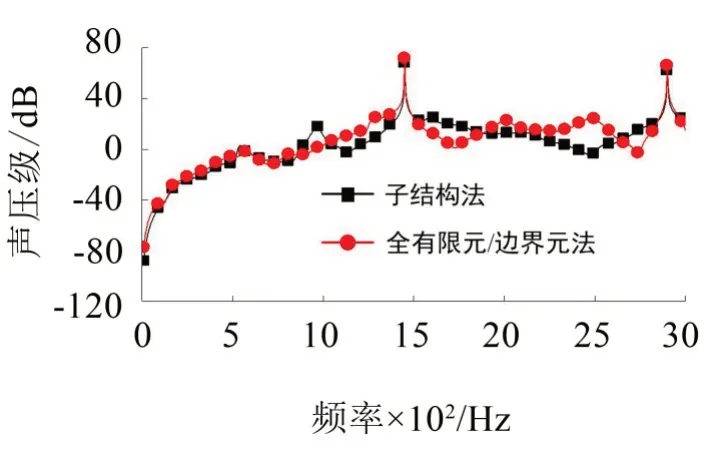
圖11 場點4上輻射噪聲頻譜對比

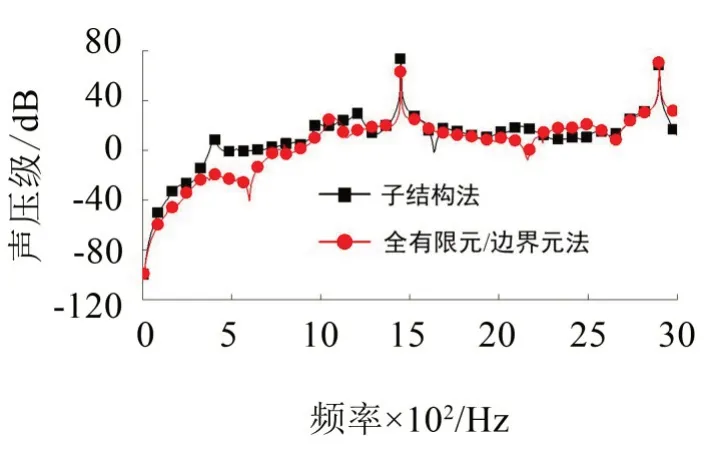
圖12 場點5上輻射噪聲頻譜對比

從表4中可以看出通過子結構法和全有限元/邊界元法分析獲得的各場點上有效聲壓級間的最大差值未超過4.5 dB（其中4個場點上的差值均未超過4 dB），證明了文中提出的基于子結構法的齒輪-箱體-基座耦合系統輻射噪聲分析模型的準確性。

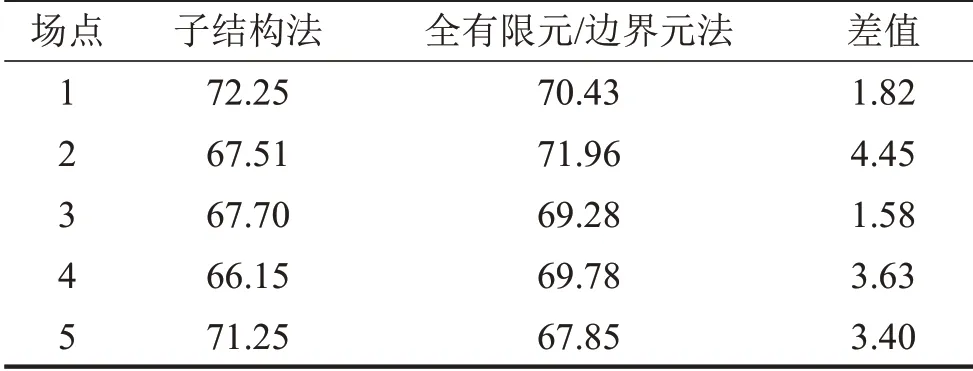
表4 不同方法獲得的各場點上有效聲壓級的對比/(dB)

在對分析結果進行對比和驗證的同時，還對兩種方法的求解時間進行了對比。結果表明對于文中的齒輪-箱體-基座耦合系統，用子結構法進行輻射噪聲分析共需要1 975 s，而用全有限元/邊界元法進行分析共需要6 034 s。采用子結構法后，計算時間縮短了67.3%。

4 結語

本文采用靜態子結構法對基座進行了等效，在此基礎上建立了齒輪-箱體-基座耦合系統的輻射噪聲分析模型，通過求解獲得了箱體-耦合系統各場點處的輻射噪聲頻譜；并與全有限元/邊界元法的分析結果進行了對比。主要結論如下：

(1)各連接點處加速度級的峰值均出現在嚙合頻率及其2倍頻處，與軸承動載荷的分布規律一致。

(2)通過子結構法分析獲得的箱體-基座耦合系統在各場點處的有效聲壓級與全有限元/邊界元法分析結果間的差距均未超過4.5 dB，證明了文中提出的用子結構法進行箱體-基座耦合系統輻射噪聲分析的準確性。

(3)結合子結構法和有限元/邊界元法進行箱體-基座耦合系統輻射噪聲分析需要的時間僅為全有限元/邊界元法的32.7 %。表明文中提出的方法方法可極大地提高計算效率。