順藤摸瓜 尋求突破

陸金花

圖形變換是中考考查內(nèi)容之一，可能以填空、選擇、解答題等題型呈現(xiàn)，具體解答時(shí)有時(shí)還需添加輔助線。下面，我們以一道圖形變換的中考題為例，來(lái)探討如何順藤摸瓜，找到解決這類問(wèn)題的突破口。

例1如圖1，在Rt△ABC中，∠B=90°，AB=，BC=將△ABC繞點(diǎn)A按逆時(shí)針?lè)较蛐D(zhuǎn)90°得到△AB′C′，連接B′C，則sin∠ACB′=_______。（3分）

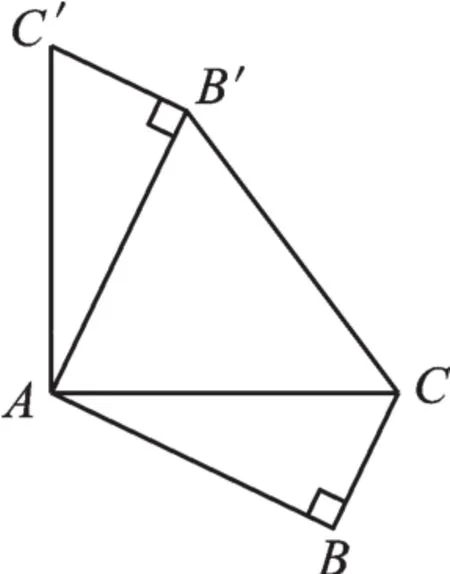
圖1

雖然本題為一道填空題，做對(duì)得3分，做錯(cuò)或不做不得分，但我們?cè)诜治鰡?wèn)題時(shí)同樣也可以剖析其考查的知識(shí)點(diǎn)，踩點(diǎn)進(jìn)行分析解答，以便順藤摸瓜，得到正確答案。

【考點(diǎn)】旋轉(zhuǎn)變換、勾股定理、相似三角形的判定與性質(zhì)、銳角三角函數(shù)的定義。

【解析】旋轉(zhuǎn)是圖形變換中的一種，旋轉(zhuǎn)問(wèn)題指的是一個(gè)圖形繞著某個(gè)點(diǎn)按順時(shí)針或逆時(shí)針?lè)较蜣D(zhuǎn)動(dòng)一定角度后，得到新的圖形，然后求解旋轉(zhuǎn)前后圖形的一些線段、角及與之相關(guān)的量。處理這類問(wèn)題的關(guān)鍵在于找到旋轉(zhuǎn)前后相等的量。本題是旋轉(zhuǎn)、勾股定理、三角函數(shù)、相似的綜合。顯然，由旋轉(zhuǎn)知△ABC≌△AB′C′，而要求sin∠ACB′的值，則將∠ACB′放置于一個(gè)直角三角形中，利用所學(xué)知識(shí)進(jìn)行求解即可。

解：在Rt△ABC中，由勾股定理可得AC=5。

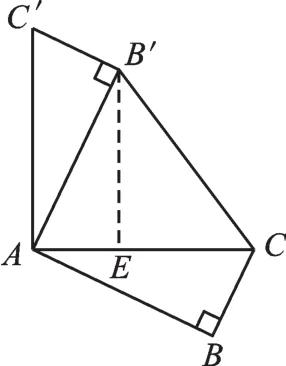
圖2

易證△B′AE∽△ACB，從而根據(jù)“相似三角形的對(duì)應(yīng)邊成比例”可求得AE=2，B′E=4。

∴CE=AC-AE=5-2=3。

在Rt△B′CE中，由勾股定理可得B′C=5。

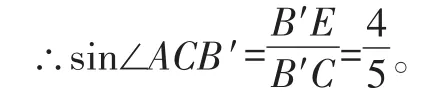
【點(diǎn)評(píng)】通過(guò)上例，不難看出，對(duì)于此類較復(fù)雜的問(wèn)題，我們需要踩點(diǎn)分析，才能順利找到解題的突破口。比如，已知一個(gè)直角三角形（△ABC）的兩邊長(zhǎng)，可以根據(jù)勾股定理求得第三邊的長(zhǎng)。再如，要求一個(gè)角（∠ACB′）的正弦值，需構(gòu)造直角三角形（△B′CE）。此外，旋轉(zhuǎn)將圖形中的基本元素（線、角）進(jìn)行了關(guān)聯(lián)，而“相似三角形的判定與性質(zhì)”則是求解這類幾何計(jì)算題的常用手段。只要我們善于抓住本質(zhì)，踩點(diǎn)分析，就一定能順利尋求突破。