送粉管道聯合吊架拉桿的設計
王 源, 溫 泉
1.上海電氣電站工程公司 上海 201100 2.中國能源建設集團 安徽省電力設計院有限公司 合肥 230601
1 設計背景
在國家持續降低供電煤耗和提高環保標準的背景下,火力發電廠不斷向高參數、大容量發展[1]。《煤電節能減排升級與改造行動計劃(2014—2020年)》中明確指出,新建燃煤發電項目原則上采用600 MW及以上超超臨界機組。
大型火力發電廠鍋爐燃燒器的數量較多,導致煤粉管道數量也較多。一般情況下,四角切圓煤粉爐共有24根煤粉管道,前后墻對沖煤粉爐共有36根煤粉管道。在煤粉管道的布置設計中,往往會出現多根管道聯合支吊的情況。
在以往的工程設計中,聯合吊架拉桿應力分析均按照《火力發電廠煙風煤粉管道設計技術規程》中的靜力矩平衡法進行計算[2]。以三拉桿聯合吊架為例,按規程進行載荷分配后,中間一根拉桿承受1/2載荷,兩邊各承受1/4載荷,最后整體按1/2載荷選型。這樣的吊架設計缺乏精確性和嚴謹性,難以適應火電廠精細化設計的發展趨勢[3-4]。
筆者建立吊架模型,根據模型的約束特點,采用結構力學中的位移法對大型送粉管道聯合吊架拉桿的受力情況進行分析,給出受力方程,并對拉桿選型進行合理優化,節省投資。
2 送粉管道布置方案
某2×660 MW火電廠采用側煤倉布置,鍋爐為前后墻對沖燃燒、二次再熱、Π型鍋爐,每墻布置三層燃燒器,標高依次為+23.225 6 m、+28.613 6 m、+34.001 6 m,每層有六臺旋流煤粉燃燒器。制粉采用中速直吹式系統,單爐配備六臺磨煤機,每臺磨煤機對應六根送粉管道,連接每層的燃燒器。
送粉管道管徑為508 mm,設計壓力為21.68 kPa,防爆設計壓力為0.4 MPa,設計溫度為110 ℃。典型的聯合吊架設置形式如圖1所示。圖1中,1為聯合吊架的管道支撐梁,2為聯合吊架生根的構筑梁,A、B、C為聯合吊架的三根拉桿,負責將聯合吊架固定在構筑梁上,P1~P6為支撐在聯合吊架上的六根送粉管道。

圖1 聯合吊架設置形式
這一工程存在大量六根送粉管道聯合支吊的情況,采用三拉桿聯合吊架后,每根拉桿的受力在材料力學上屬于超靜定問題,以往不對此類問題進行分析研究,導致吊架選型不合理。筆者以此類三拉桿聯合吊架為例進行分析。
3 聯合吊架拉桿受力分析
3.1 受力分析方法
當吊架組件所受應力的值達到或超過材料強度極限時,材料可能產生開裂、變形、斷裂、失穩等現象[5-6],將導致吊架失效或被破壞。而若盲目選擇高規格的吊架組件,則會造成建設資金的浪費。聯合吊架拉桿受力分析的目的是對吊架超靜定受力工況進行力學分析,使吊架組件在設計要求的載荷作用下,有效抵抗不被允許的變形和破壞,在保證管道和吊架安全性的同時,兼顧經濟性的需求。
超靜定結構體系的內力計算方法依據靜力平衡條件和變形協調條件,可分為兩大類:力法和位移法[7-8]。力法以力為基本未知量,釋放關鍵點的約束,以未知力表示關鍵點的位移,根據變形協調條件,求出關鍵點的未知力,從而求出整個結構的內力。位移法以位移為基本未知量,約束關鍵點,依據變形協調條件,以未知位移表示關鍵點的力,再根據關鍵點的靜力平衡條件,求出關鍵點的位移,從而求出整個結構的內力[9]。
力法出現得較早,只用于計算超靜定結構。位移法出現得稍晚,適用于靜定和超靜定體系,計算時的收斂性更好,并且位移法每個步驟都有明確的物理意義,有助于理解和記憶。后期出現的力矩分配法和無剪力分配法都屬于位移法的范疇。鑒于位移法的諸多優點[10],筆者考慮采用位移法進行分析計算。
3.2 建模
以管道支撐梁的受力情況為研究對象建立模型,圖1所示某2×660 MW火電廠典型聯合吊架設置形式可簡化為圖2所示模型。
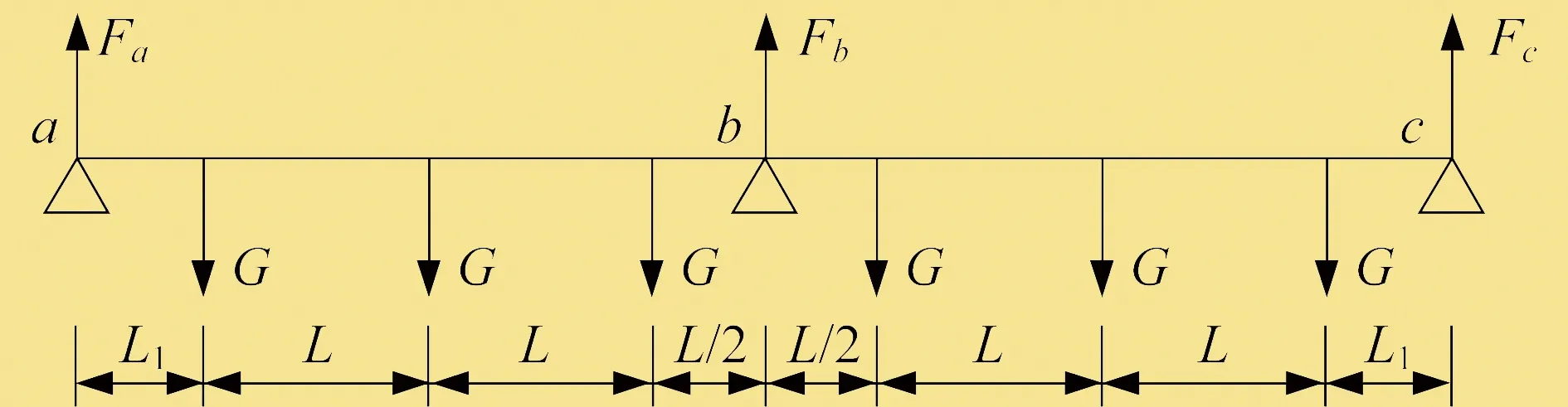
圖2 聯合吊架簡化模型
圖2中,a點、b點、c點代表三根拉桿在管道支撐梁上的拉力作用點,Fa、Fb、Fc依次為A、B、C三根拉桿施加在管道支撐梁上的拉力,L為送粉管道之間的中心距,L1為最外側送粉管道中心至拉桿的距離,G為單根送粉管道載荷。
3.3 解析計算
解析計算主要依據結構力學中的位移法進行。位移法以控制節點的位移為基本未知量,用位移表示控制節點處的力,根據節點處靜力平衡條件,求出控制節點的位移,進而求出結構內力。位移法計算主要分為三步。第一步,通過在控制節點施加約束,將結構拆為獨立的桿件基本結構。在外力的作用下,對各獨立桿件進行結構分析,求出各獨立桿件中控制節點處的約束力。第二步,通過對控制節點施加與原結構位移相同的位移,對各桿件進行結構分析,求出位移作用下控制節點處的力。第三步,將前兩步求出的力進行疊加,并根據控制節點處的靜力平衡條件,求出控制節點處的位移,進而求出結構內力。
由圖2可以看出,該聯合吊架模型為連續梁結構,將b點作為關鍵節點,b點只有角位移,沒有線位移,因此這一結構屬于無側移框架體系。
根據位移法的計算步驟,在b點上施加轉動約束,形成模型基本結構,如圖3所示,進而將連續梁拆分成ab桿和bc桿兩個獨立的桿件,由此可以分別計算在送粉管道載荷G作用下獨立桿件ab桿和bc桿中b點的約束彎矩MabG、MbcG。對控制節點施加角度,直至各獨立桿件的變形與原結構變形一致,形成模型基本體系,如圖4所示。設此時b點產生的角位移為θb,由此可以計算出角位移θb在ab桿和bc桿中b點產生的彎矩Mabθ和Mbcθ。將以上兩個步驟計算得到的彎矩疊加,并考慮b點的彎矩平衡,列出平衡方程。在該方程中,僅有角位移θb一個變量,可順利求出θb,從而求出該結構在a點、b點、c點處的反力。在計算過程中,約定彎矩方向以順時針為正,以逆時針為負。

圖3 模型基本結構
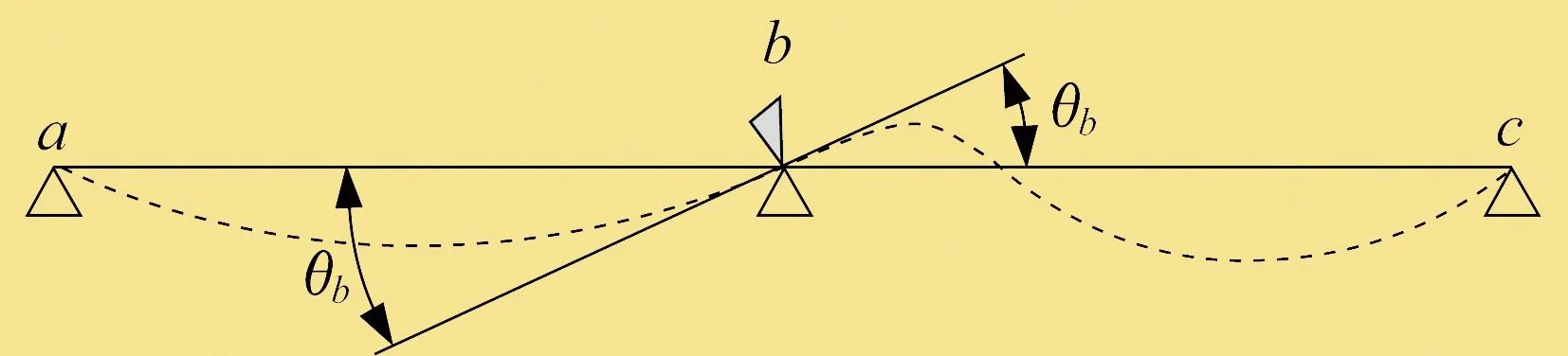
圖4 模型基本體系
對獨立桿件ab桿和bc桿進行計算,根據結構力學中彎矩的計算公式,可以計算出由送粉管道載荷G引起的基本結構中的彎矩:
MabG=-αGL
(1)
MbcG=αGL
(2)
(3)
b點彎矩方向如圖5所示。
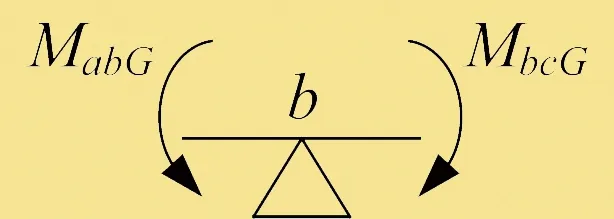
圖5 送粉管道載荷引起的b點彎矩方向
對b點施加角位移θb,當角位移θb與原結構在送粉管道載荷G作用下的角位移相同時,約束力為0,即等效于原結構,則由角位移θb引起的b點彎矩Mabθ及Mbcθ為:
Mbaθ=Mbcθ=3iθb
(4)
i=EI/L
(5)
式中:i為獨立桿件ab桿和bc桿的線剛度;E為桿件材料的彈性模量;I為桿件的慣性矩。
在實際應用中,ab桿和bc桿的規格、材質是相同的,因此兩根桿件的線剛度i相等。
由角位移θb引起的b點彎矩方向如圖6所示。
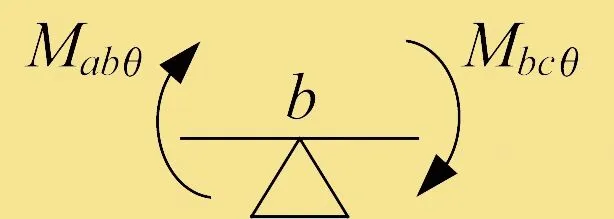
圖6 角位移引起的b點彎矩方向
將以上兩個步驟求得的彎矩分別疊加:
Mab=Mabθ+MabG=3iθb-αGL
(6)
Mbc=Mbcθ+MbcG=3iθb+αGL
(7)
在原結構中,b點受力是平衡的,由b點彎矩平衡可得Mab+Mbc=0,θb=0。因此,b點兩側彎矩Mab、Mbc為:
Mab=-αGL
(8)
Mbc=αGL
(9)
對b點左側取彎矩,得到獨立桿件ab桿的受力,如圖7所示。
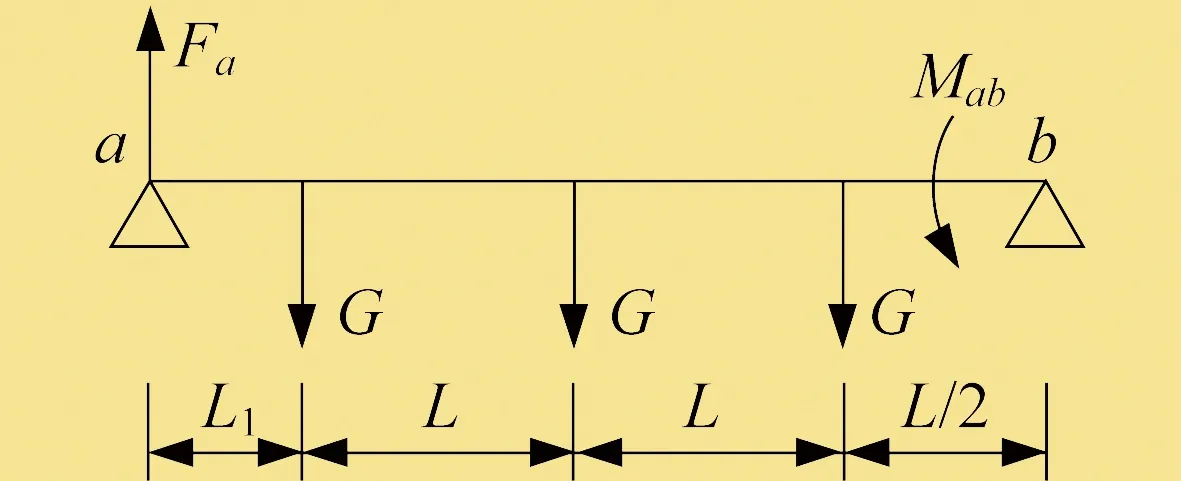
圖7 ab桿受力
由圖7可得:
同理得:
(12)
由原結構受力平衡,可得:
Fa+Fb+Fc=6G
(13)
(14)
根據上述推導計算,a點、b點、c點的支座反力計算式,即拉桿受力計算式見表1。表1中均為參數化表示,方便在不同的工程中應用。

表1 拉桿受力計算式
4 優化算法討論
通過以上建模與推導,可以得出送粉管道聯合吊架三根拉桿所承受的拉力Fa、Fb、Fc。由于L1的取值對拉桿受力存在較大影響,因此結合工程實際分三種工況進行探討。
(1)L1=L時,邊界條件為L1=L=880 mm,G=15.68 kN,且Fa=Fc=291G/343,Fb=6G-582G/343。
由傳統靜力矩平衡法與位移法所計算出的拉桿受力及拉桿選型見表2,拉桿型號根據《發電廠汽水管道支吊架設計手冊(D-ZD2010)》選取,以拉桿直徑大小表示[11]。
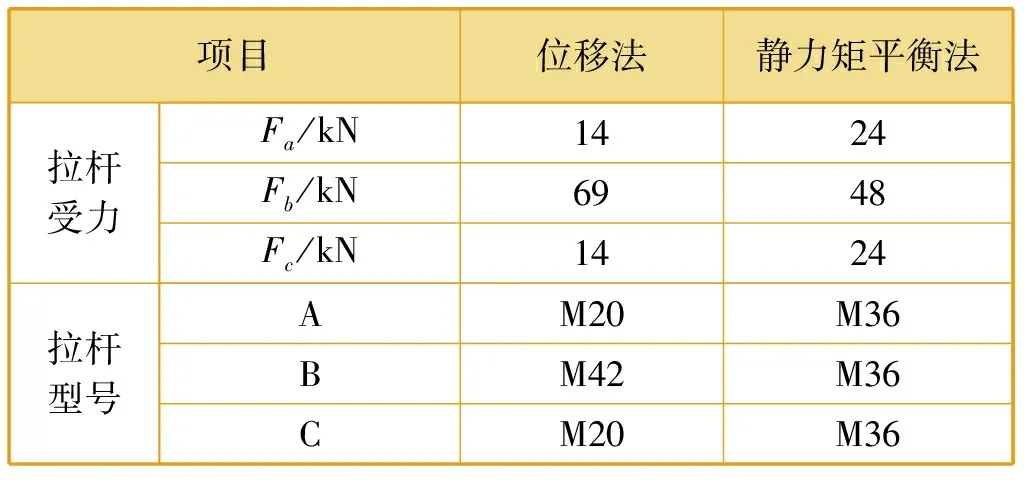
表2 L1=L時計算結果比較
由表2可知,靜力矩平衡法以拉力Fa、Fb、Fc中最大者為選型載荷,導致拉桿A、C選型過大,比位移法選擇的A、C拉桿型號大三檔,造成材料浪費。靜力矩平衡法對拉桿B所受拉力值估算偏小,拉桿選型比位移法小一檔,在后期運行中可能會導致拉桿B相關組件,如拉桿、螺母、花籃螺釘、單耳吊板等變形失效和破壞,存在較大的安全隱患。
(2)L1>L時,邊界條件為L=880 mm,L1=1 500 mm,G=15.68 kN。
由傳統靜力矩平衡法與位移法所計算出的拉桿受力及拉桿選型見表3。

表3 L1>L時計算結果比較
由表3可知,隨著L1的增大,拉桿A、C的受力Fa、Fc持續減小,再按靜力矩平衡法選擇拉桿型號明顯不合理,采用靜力矩平衡法得到的拉桿選型比位移法大四檔。此外,當L1>L時,靜力矩平衡法對拉桿B所受拉力值估算偏小,選型不合理,存在安全隱患。
(3)L1 由傳統靜力矩平衡法與位移法所計算出的拉桿受力及拉桿選型見表4。 表4 L1 由表4可知,當L1減小到一定程度后,靜力矩平衡法得出的拉桿B所受拉力Fb與位移法計算結果接近,拉桿選取型號可保持一致。如果通過位移法精確計算出Fa、Fc,并據此選型,那么可以選出比靜力矩平衡法小兩檔的拉桿型號,節省了一定的材料。 對于大型送粉管道聯合吊架的拉桿設計,以往通過《火力發電廠煙風煤粉管道設計技術規程》中的靜力矩平衡法來分配拉桿載荷,吊架選型不合理、不精確,常常會導致選型偏差較大,造成材料浪費,甚至影響運行安全。筆者通過建立聯合吊架力學計算模型,推導出三拉桿超靜定體系吊架的受力解析計算式,通過與靜力矩平衡法對比,得出結論。當L1≥L時,應采用位移法進行吊架載荷計算,可以有效提高送粉管道運行的可靠性,降低吊架成本。當L1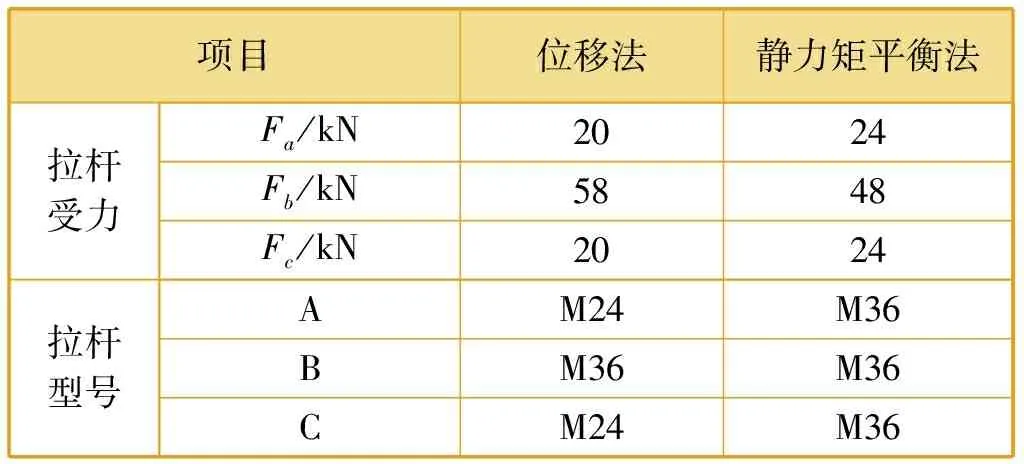
5 結束語

