一種基于SATA的無線傳感器網絡定位算法*

梁森 王志宏 唐王龍 李昌鎬 張明

?

一種基于SATA的無線傳感器網絡定位算法*

梁森1王志宏1唐王龍1李昌鎬2張明3

（1.中建四局第一建筑工程有限公司 2.中山大學 3.廣東郵電職業技術學院）

在無線傳感器網絡中，將節點定位看作一種地球物理反演問題，即一種求全局最優解問題，并將原子尋求最穩定狀態的躍遷過程，應用于求解節點的最優位置過程，提出一種無線傳感器節點定位算法——模擬原子躍遷定位算法。針對不同噪聲環境進行仿真實驗，實驗結果表明：與模擬退火算法對比，本文提出的算法在定位精度和定位效率上有更好表現。

無線傳感器網絡；定位；物理反演問題；模擬原子躍遷算法

0 　引言

近年來，無線傳感器網絡受到越來越多的關注。隨著微機電技術的快速發展，無線傳感器網絡的節點終端更加智能、輕便、低能耗，且具有測量、感知和收集外界環境信息等功能[1]。無線傳感器網絡在國防科技、智能家居、共享經濟和防火救災等領域有較大的實用價值[2]，并被認為是繼互聯網之后，二十一世紀最重要的技術之一[3]。

無線傳感器網絡中的節點定位實際上也是在區域范圍內尋求最優坐標點問題，故可當作物理反演問題來處理。王家映[4-5]等提出一種模擬原子躍遷算法（simulated atomic transition algorithm, SATA），用于解決地球物理反演問題中的非線性最優化問題，并通過理論及實驗分析證明了此算法的可用性。文獻[6]根據蒙特卡洛算法（Monte Carlo algorithm, MCA）提出一種移動設備的定位算法。文獻[7]提出一種基于模擬退火算法（simulated annealing algorithm, SAA）。文獻[8]提出一種基于模擬植物生長的定位算法。這些定位算法在理想情況下能得到較好的定位效果，但存在噪聲時，可能得到局部最優值，而非全局最優值。

本文把未知節點定位當作是求全局最優解問題考慮。基于SATA，提出一種無線傳感器網絡定位算法——模擬原子躍遷定位算法。通過未知節點的定位問題與原子躍遷過程的類比分析，定義目標函數；然后運用SATA求取此目標函數的最優解，即未知節點的位置坐標；最后通過與SAA比較，分析本文提出的模擬原子躍遷定位算法的定位性能。

1　SATA

根據原子量化模型理論，當原子處于平衡穩定狀態時，核外電子在各個能級軌道上的分布服從玻爾茲曼（Boltzmann）分布[9]。電子在不同能級之間躍遷概率公式為

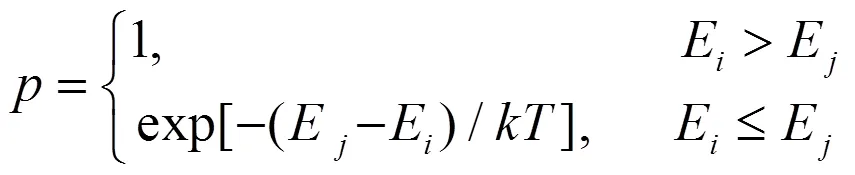
原子的各個能級可通過式(2)計算得到：

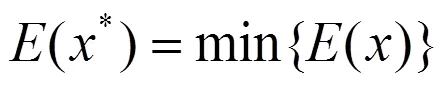
原子能量函數、原子能級圖如圖1、圖2所示。

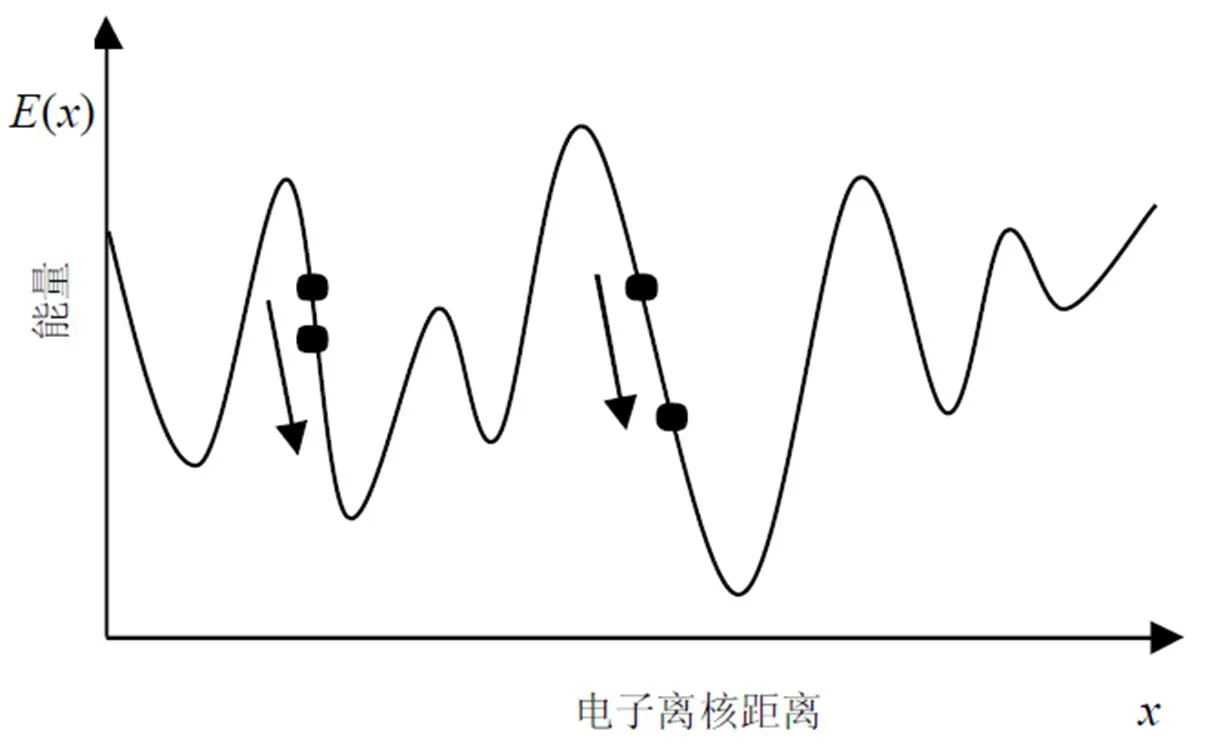
圖1 　原子能量函數

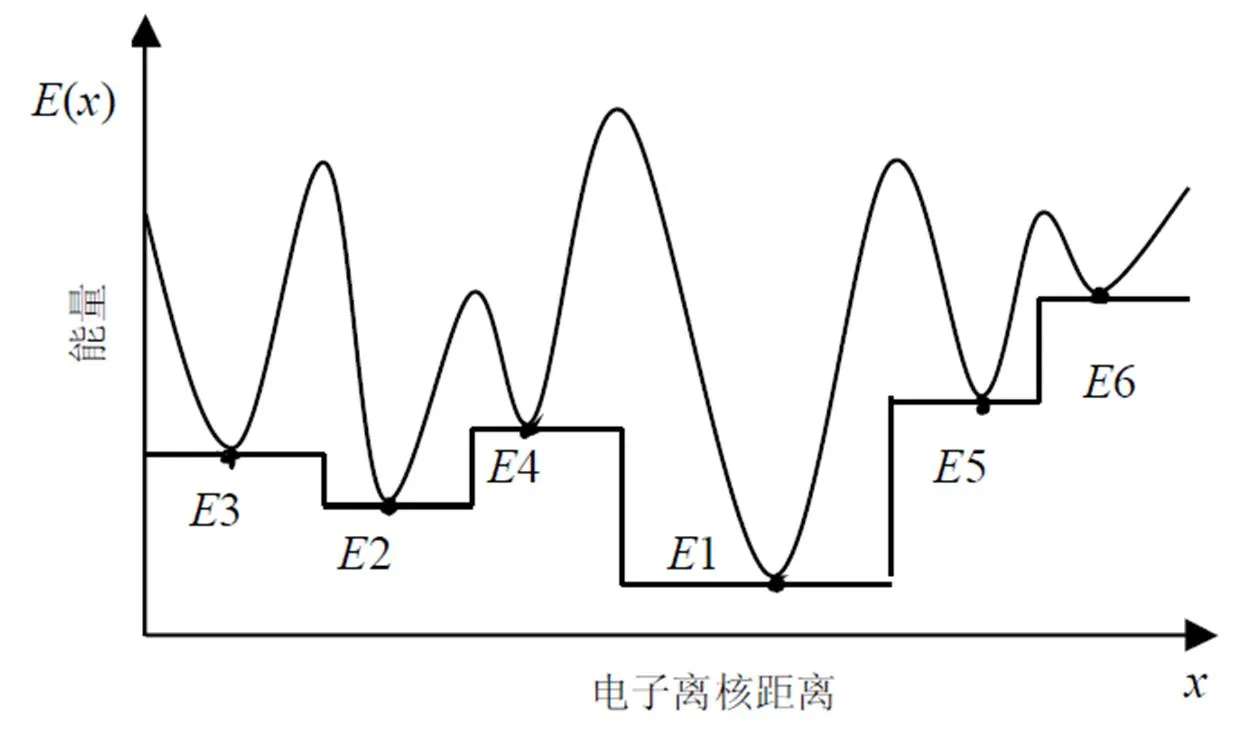
圖2　 原子能級圖

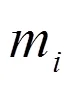
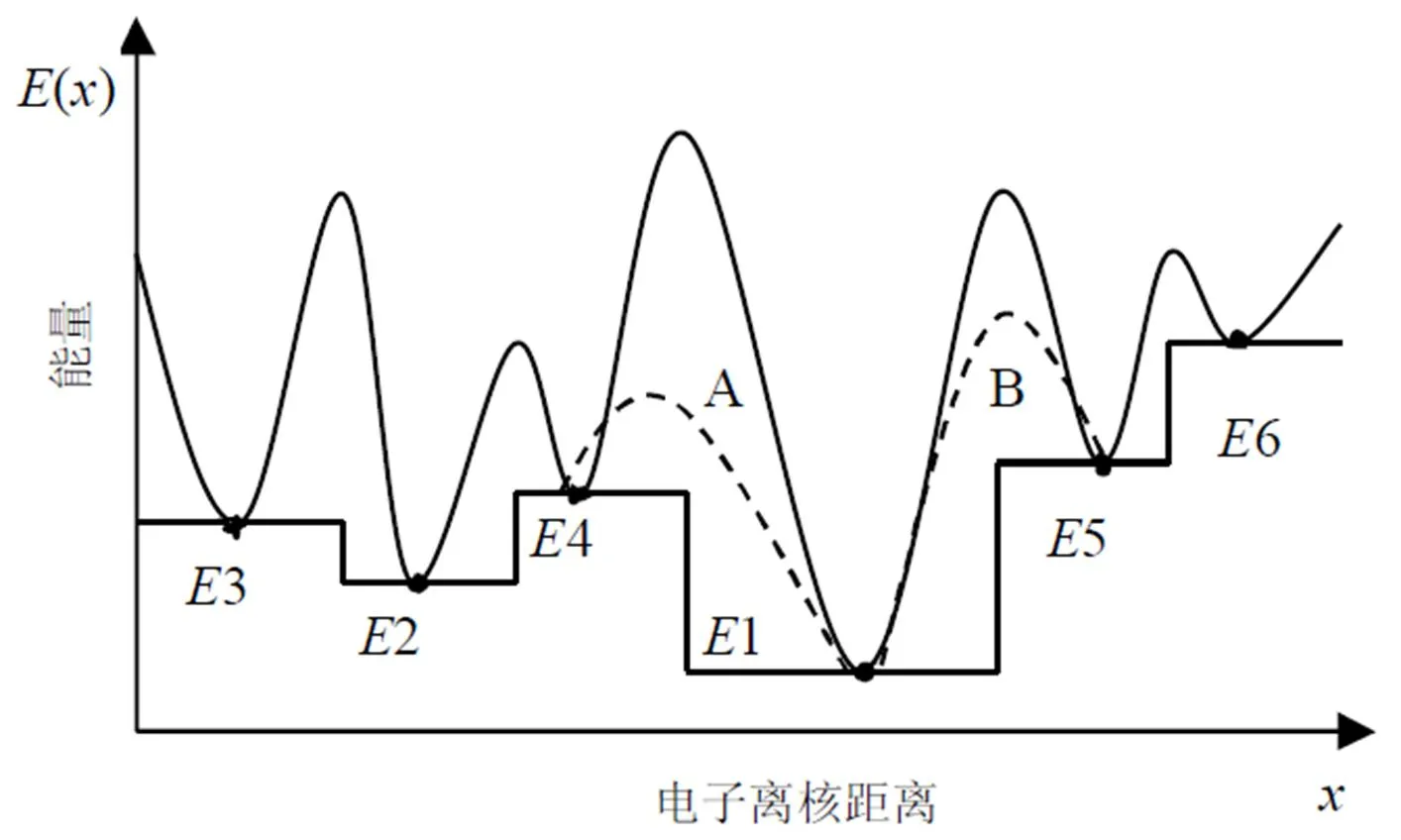
圖3　 原子躍遷過程

上述躍遷可能僅使原子處于能級較低的狀態，并非是能量最低的穩定基態，即所得結果是局部最優解。為了能利用上一次躍遷的信息，可在前一次躍遷的基礎上進行粒子轟擊得到新的躍遷參數。粒子轟擊可按式(3)添加一隨機數進行擾動，即

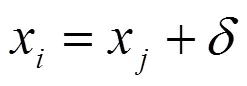
如此反復躍遷，直至達到設定條件，所得結果即為最優解。

模擬原子躍遷求取全局最優解的具體步驟：

1）基于目標問題構建目標能量函數，隨機給定目標問題的初始參數值群體；

2）求各個參數值對應的目標能級，如果目標能級小于給定的閾值，則直接跳轉到步驟5），否則繼續執行步驟3）；

3）根據目標能級比較和躍遷概率計算的結果，進行原子躍遷；

4）進行隨機粒子轟擊，以便產生新的參數值群體，跳轉到步驟2），開始進行新一輪躍遷；

5）當滿足躍遷結果條件（躍遷至最低能級或者達到最大迭代次數）時，輸出最優解。

2　模擬原子躍遷定位算法

在無線傳感器網絡中，根據節點位置是否已知，可將節點分為2大類：一類是位置坐標已知的節點，稱之為信標節點；另一類是待確認位置的未知節點。其中信標節點主要用于通過一定算法來估算未知節點的位置信息。

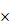
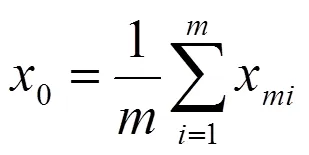
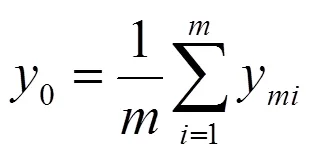
根據模擬原子躍遷定位算法，未知節點定位的目標函數設為

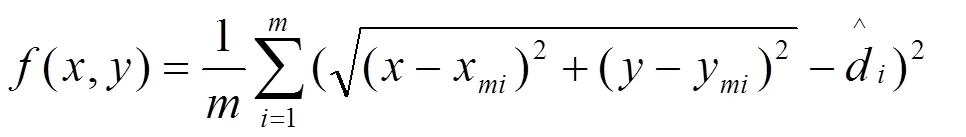
未知節點定位過程與原子躍遷過程的對應關系如表1所示。

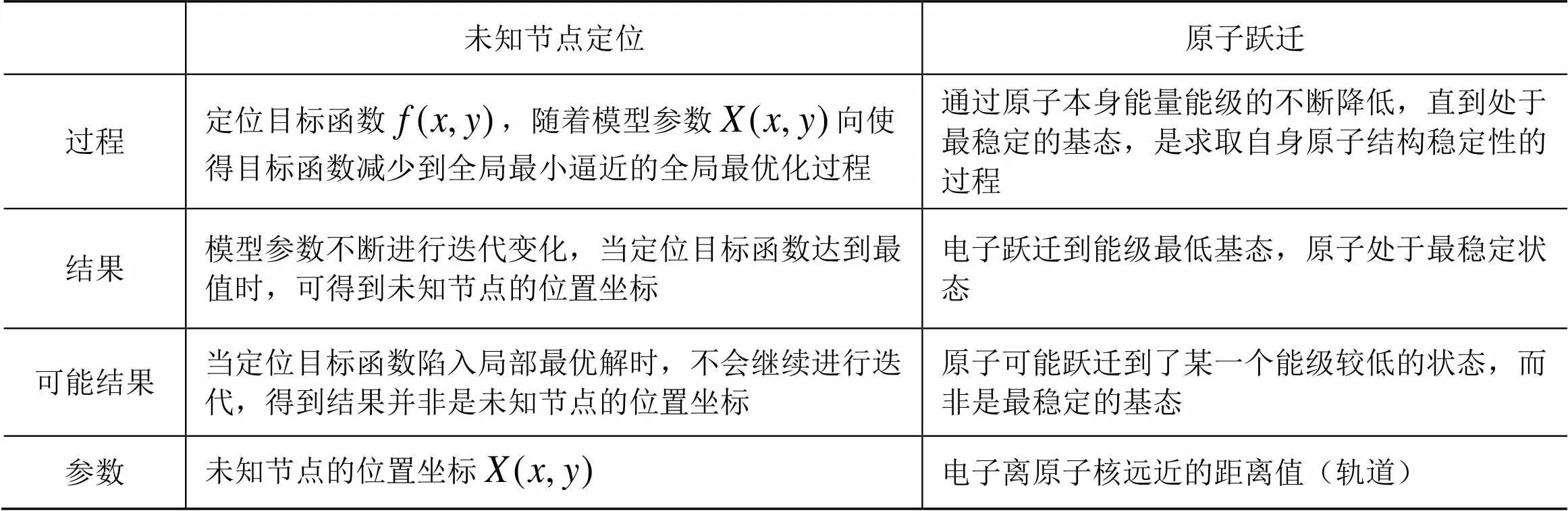
表1　 未知節點定位過程與原子躍遷過程的對應關系表

3　仿真與分析

本文通過Matlab仿真模擬原子躍遷定位算法和SAA，并進行比較。

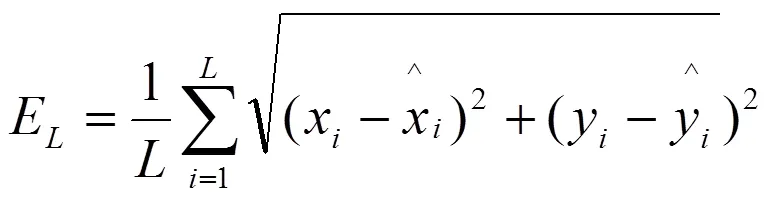
1）同樣誤差情況的表現

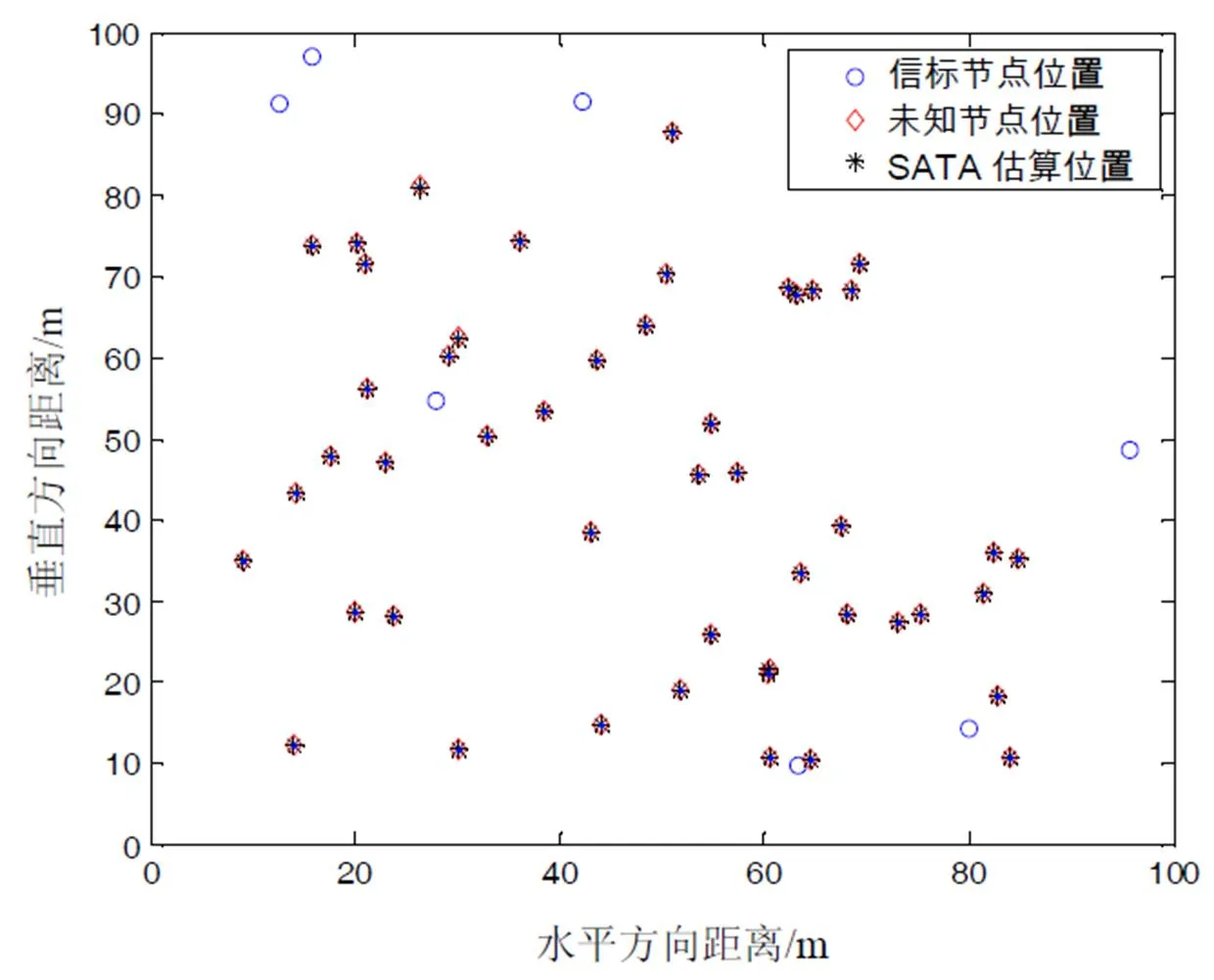
圖4 理想情況下，模擬原子躍遷定位算法仿真結果

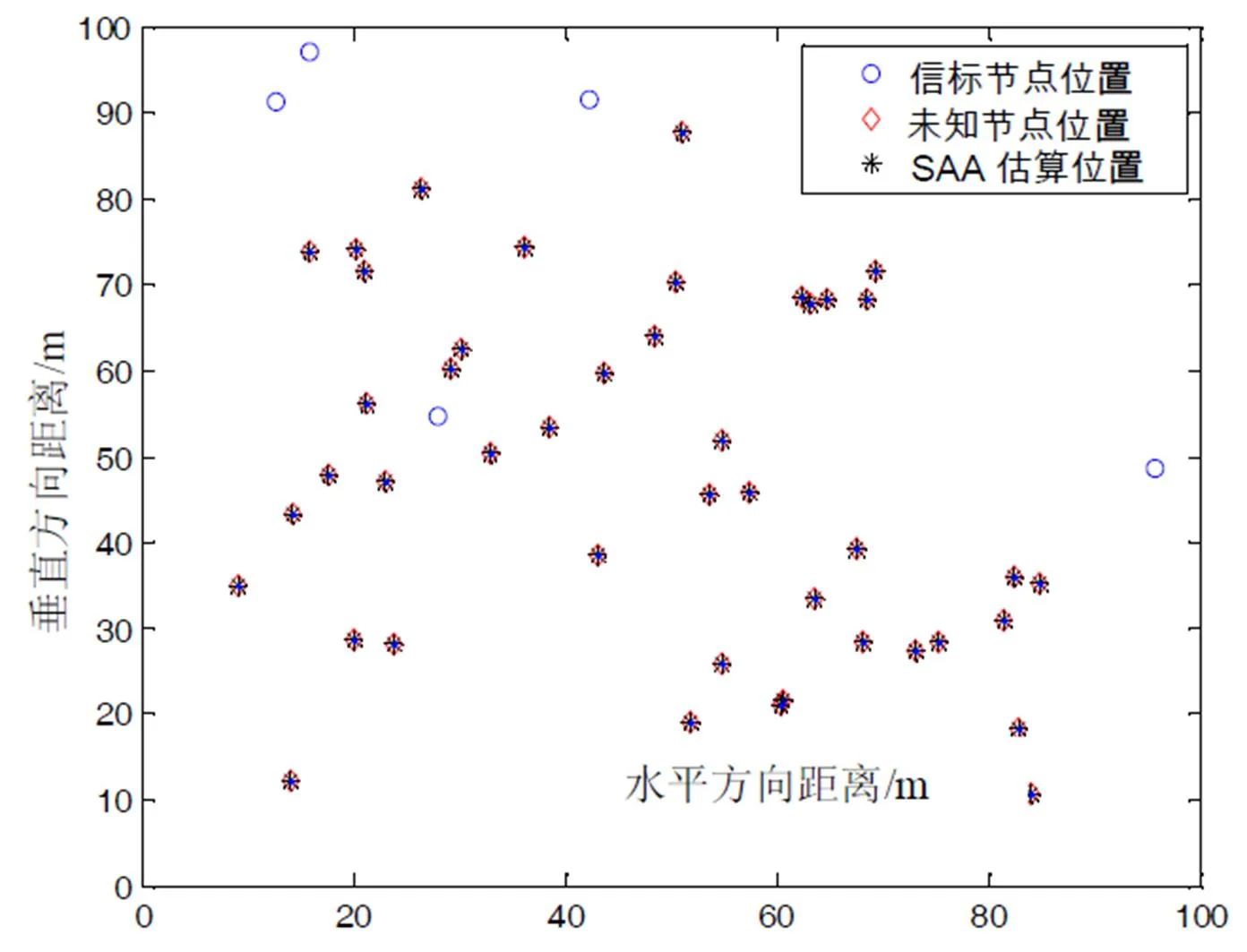
圖5 理想情況下，SAA 仿真結果

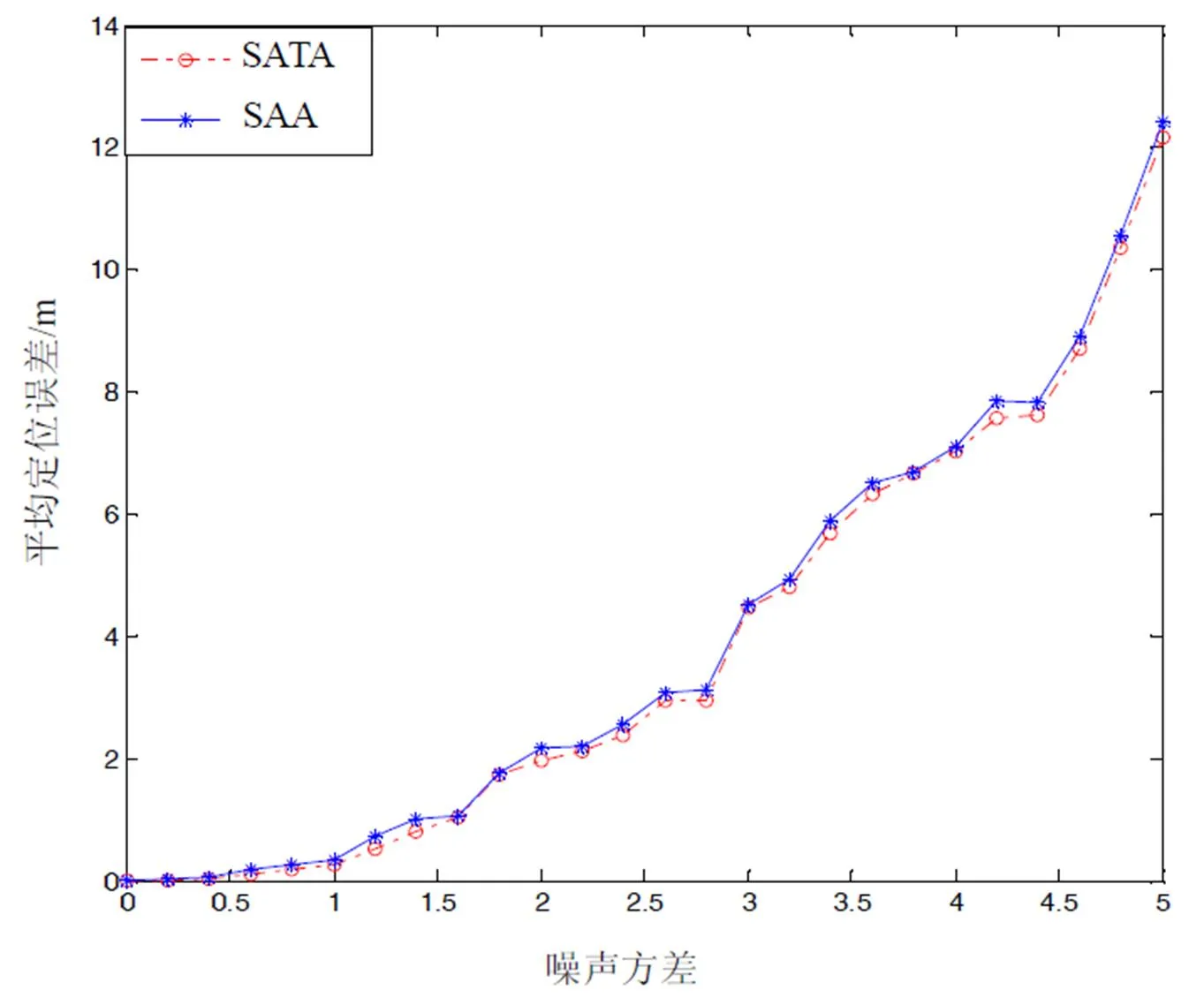
圖6 不同噪聲時，SAA 與模擬原子躍遷定位算法仿真效果

2）定位時間

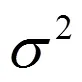
4　結論

本文提出一種模擬原子躍遷定位算法。該算法將節點定位看作一種求全局最優解問題。為防止得到局部極小值而非最優值，在模擬原子躍遷過程中，引入粒子轟擊，加入隨機數。從仿真結果看出，與SAA相比，本文算法不僅可以提高定位精度，還可以提高定位速度。隨著無線傳感器網絡的發展，本算法其定位方面有較好的應用前景。

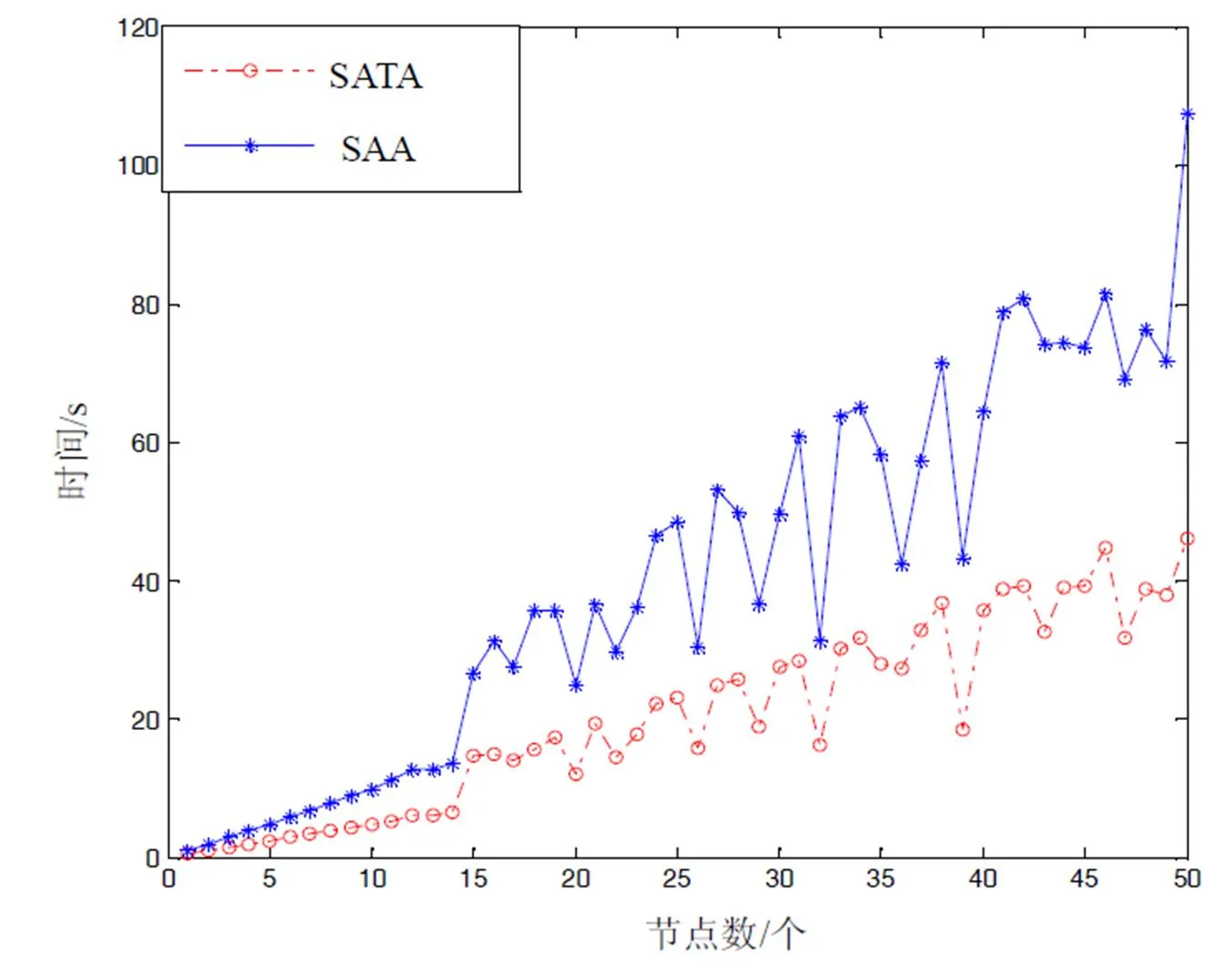
圖7 SAA與模擬原子躍遷定位算法定位性能比較

[1] Darwish A, Hassanien A E. Wearable and implantable wireless sensor network solutions for healthcare monitoring[J]. Sensors, 2011,11(6): 5561-5595.

[2] 傅留虎,胡欣宇.智能傳感器中的算法應用[J].物聯網技術,2017,7(2):15-17,21.

[3] 彭宇,王丹.無線傳感器網絡定位技術綜述[J].電子測量與儀器學報,2011,25(5):389-399.

[4] 師學明,王家映,易遠元,等.一種新的地球物理反演方法——模擬原子躍遷反演法[J].地球物理學報,2007,50(1):305-312.

[5] Dai Yuhong, Kou Caixia. A nonlinear conjugate gradient algorithm with an optimal property and an improved Wolfe line search[J]. SIAM Journal on Optimization, 2013,23(1): 296-320.

[6] Wang Jia, Fu Jingqi. Research on APIT and Monte Carlo method of localization algorithm for wireless sensor networks[J]. in Life System Modeling and Intelligent Computing, 2010:128-137.

[7] Pal A. Localization algorithms in wireless sensor networks: current approaches and future challenges[J]. Network Protocols & Algorithms, 2010, 2(1).

[8] Tang, C P, Liu R Q, Ni J Q. A novel wireless sensor network localization approach: localization based on plant growth simulation algorithm[J]. Electronics & Electrical Engineering, 2013,19(8).

[9] 聶承昌.玻爾原子結構理論及其歷史中介意義[J].華南師范大學學報(社會科學版),1997(2):9-14.

A SATA-Based Localization Algorithm for Wireless Sensor Network

Liang Sen1Wang Zhihong1Tang Wanglong1Li Changhao2Zhang Ming3

(1.The First Construction Co., Ltd. of China Fourth Construction Bureau 2.Sun Yat-sen University 3.Guangdong Vocational College of Post and Telecom)

In recent years, the application scenarios and scope of IoT technology have become wider and wider. Wireless sensor networks, one of the core technologies of IOT, also play an important role in all walks of life, with high research and economic value. In the field of wireless sensor network technology, how to get the exact location of nodes is a key issue that practitioners in industry and academia pay particular attention to. Based on the in-depth study of node localization problems and physical inversion problems, this paper proposes to regard node localization as a geophysical inverse problem, which is a global optimal solution problem. Through the study of the atomic transition process in physics, this paper applies the "transition" process of atom seeking the most stable state to the optimal position of the solution node, and proposes a new wireless sensor node localization algorithm - Simulated Atomic Transition Algorithm (SATA). Compared with Simulated Annealing Algorithm (SAA) under ideal conditions and different noise conditions, the proposed algorithm has better performance in positioning accuracy and efficiency.

Wireless Sensor Network; Localization; Geophysical Inverse Problem; SATA

梁森，1982年生，男，高級工程師，碩士學歷，主要研究方向：項目管理。

王志宏，1990年生，男，助理工程師，碩士學歷，主要研究方向：工程建設、技術管理。

唐王龍，1983年生，男，工程師，碩士學歷，主要研究方向：建設工程、技術管理。

李昌鎬，1995年生，男，研究生，主要研究方向：深度學習、多模態數據融合等。

張明（通信作者），1989年生，男，助教，碩士學歷，主要研究方向：邊緣智能、數據挖掘等。E-mail: huake_zhming@163.com

廣東省自然科學基金（2018A030313797）；廣東省科技計劃項目（2016B010125001，2016B090918110，2014B090901057）。