基于核空間加權稀疏表示的滾動軸承故障診斷

錢 猛,呂衛民

(海軍航空大學 岸防兵學院, 山東 煙臺 264001)

滾動軸承是汽車傳動系統，風力發電機組，航空發動機，機床等電機和旋轉機械的關鍵部件。這些裝置通常在高速，重載，高低溫和污染的惡劣的工作條件下工作，希望執行在線狀態監測以提高其可用性，安全性和可靠性，降低運行和維護成本，并實現停機時間最小化和生產力最大化。 由于這些設備中的許多故障可能從滾動軸承故障開始，因此有效的故障診斷可以防止災難性事故。

目前主要有兩類故障診斷模型：基于故障物理模型和數據驅動模型。基于故障物理的故障診斷方法試圖解構軸承的機制來確定故障類型。 由于復雜的故障誘因，故障模式可能是強非線性甚至混沌的。在這種情況下，很難建立基于物理的故障診斷模型。與基于物理的模型不同，數據驅動的方法僅依賴于監測數據和構建模型來反映歷史數據與故障類型之間的關系。由于傳感器的發展，可以實現大量的測量數據。使用這些數據，數據驅動的模型可以提取反映受監控組件運行狀態的信息。與基于物理的模型相比，數據驅動的方法對故障機制或操作條件的依賴性較小，因此在沒有專業知識的情況下構建它們會更簡單但更普遍。

主成分分析[1]和Fisher線性判別方法作為數據驅動方法首先被引入故障診斷。然而，這兩種方法都是線性方法，強烈的非線性故障增長機制使得在軸承診斷中表現不佳。人們進而提出了一些非線性方法，如人工神經網絡(ANN)[2]和隱馬爾可夫模型(HMM)[3]。然而，這些方法需要大量具有各種故障類型的歷史數據來訓練這些模型，這在航空航天等一些關鍵領域中并不實用。不同于傳統診斷方法，稀疏表示(SR)[4]具有良好的適應性和高度的靈活性，能夠在冗余和過完備的字典上基于原子分解描述任意復雜信號，因此不受正交基限制，并且提供了一種有效的特征提取方法。SR理論為我們提供了一種新的特征提取模式，并在機器學習，統計學，圖像處理等許多應用領域得到了廣泛的研究。稀疏表示理論具有強大的自適應提取特征能力，為解決初期軸承故障診斷問題提供了一條有效途徑。

傳統的SRC模型忽略了測試樣本和每個字典原子之間的距離相似性。和訓練樣本更近或者更相似的訓練樣本在表示測試樣本時起到更重要的作用。為了提高原始SRC模型的判別能力，盧燦義通過將樣本的局部結構信息集成到一個統一的公式中，擴展了原始的SRC模型，并提出了加權稀疏表示(WSRC)模型[5]。WSRC自適應地利用測試樣本和每個字典原子之間的相似性來表示測試樣本。但是軸承振動信號中包含大量的非線性振動信號，這給SRC和WSRC帶來了不小的挑戰。相關文獻表明基于核技巧的算法能夠有效地解決非線性問題。 支持向量機是最著名的基于內核的方法，它結合了稀疏誘導技術和內核技巧。通過內核技巧，通過將非線性可分離特征映射到高維特征空間，基于內核稀疏表示的分類(KSRC)[6]算法被提了出來。 KSRC克服了SRC不能處理非線性信號的問題，具有更好的分類能力。

本研究在稀疏表示的基礎上提出一種新的故障診斷方法，克服了上述故障診斷方法的不足，有效地提高了故障診斷的準確率。作為稀疏分類方法的延伸，基于核空間稀疏分類方法(KSRC)將非線性振動數據映射到高維空間來提高分類準確率，在基于稀疏表示理論的滾動軸承故障診斷應用中起到了顯著的作用；然而該方法卻忽略了振動信號局部結構所包含更多的區分性信息，本文分提出一種基于核空間的加權稀疏表示軸承故障診斷方法(LMNN-WKSRC)。首先通過核函數將非線性振動信號映射到高維空間；然后通過LMNN方法提取振動數據的局部信息并求得相似度加權矩陣；最后通過優化方法求解測試樣本的稀疏系數，并通過最小化原始樣本與重構樣本之間的誤差獲得分類結果。通過軸承實驗驗證了所提算法的有效性。

1 稀疏分類模型和核稀疏分類模型

稀疏表示作為一種信號重構的方法，在人臉識別和檢測等應用領域成為研究的熱點。設Xi=「Xi,1,Xi,2,…Xi, j…Xi,ni?由第i類(共k類)訓練樣本組成的集合，ni為類內樣本總數。其中xi, j∈Rm，m為樣本維數。如果第i類訓練樣本充足，則任意屬于第i類且不在訓練集中的樣本信號可由同類訓練樣本線性表示，即：

y=αi,1xi,1…+αi, jxi, j…+αi,nixi,ni

(1)

其中：αi, j為線性表示系數；k為訓練樣本總類別數。可將上述公式可重新表示為y=Xα0，其中α0=「0,…,0,αi,1,αi,2…,0,…0?∈Rn，α0的維數為訓練樣本個數總和，而且α0中只有與第i類訓練樣本相關的系數是非零的，即在整體訓練集X上的稀疏系數是稀疏向量。

對于包含n組基(每組基作為一列)的超完備字典X∈Rm×n(n?m)，給定的信號y可以由這些基的稀疏線性組合所表示:y≈Xα，并且滿足||y-Xα||2≤ε。由于X是過完備的，所以滿足||y-Xα||2≤ε的解有無數個。因此，可以引入一個約束來獲得唯一的解。優化模型可表示為：

(2)

在滿足RIP條件下將上述優化模型轉化為以下優化模型：

(3)

對于k類問題，將n列m維特征向量構成訓練字典X∈Rm×n，用Xk代表字典X的k類nk個列向量。對于給定y∈Rm，可以由上述模型求解最優解α。進而通過下式求得y所屬類別：

(4)

其中，αk是對應于類k的α中的分量。稀疏表示模型和判決標準在人臉識別中被稱為基于稀疏表示的分類(SRC)[7]。

盡管SRC在軸承故障診斷中取得不錯的效果，但SRC無法針對滾動軸承高維非線性信號做出更進一步的識別。KSRC作為SRC的非線性擴展，通過將原始數據映射到內核空間，在滾動軸承故障診斷方面取得了不錯的效果。在基于內核的算法中，無需知道具體映射函數，最重要的是將數據映射到高維內核空間的內核技巧。一般情況下，Mercer核K∈Rn×n被用于計算內核矩陣K∈Rn×n和向量k(·，·)∈Rn，如式(5)、式(6)所示

Ki, j=k(xi,xj)

(5)

k(·,y)=[k(x1,y),…,k(xn,y)]T

(6)

xi和xj都代表訓練集。對于大量的訓練樣本，核空間較高的維度會增大計算的復雜度。因此，一般用KPCA或KLDA來降低KSRC中的維數，并且獲得變換矩陣B∈Rn×d，其中d是減小了的特征空間的維數。系數向量可以在低維核特征空間中計算，如式(7)所示

(7)

(8)

2 基于核空間加權稀疏表示的信號分類

在故障診斷中，一個好的分類方法應該具有魯棒性并且能夠從振動信號中獲得較多的區分性信息進行分類。本節提出了稀疏分類算法(SRC)的延伸算法，加權內核稀疏表示分類(LMNN-WKSRC)。該算法利用更多的區分信息來識別測試樣本。

2.1 非線性映射

與傳統的線性算法相比，在模式識別和機器學習方面對它們進行非線性轉換能對顯著提高算法的效果。非線性變換中，基于內核的方法由于具有對非線性數據的處理能力而受到廣泛的研究。對于訓練樣本X和任何測試樣本y的集合，采用非線性映射函數φ將輸入數據映射到核特征空間。由于非線性映射函數φ不容易確定，基于內核技術的方法使用Mercer內核k(·,·)來獲得高維內核特征空間中的映射數據。對于任何樣本z1和z2，具體可以表示如下

k(z1,z2)=φ(z1)Tφ(z2)

(9)

線性核和高斯徑向基函數和是用的最多的兩種Mercer內核方法。 線性核是非參數核，而高斯徑向基函數(RBF)具有可以調整核矩陣的參數

(10)

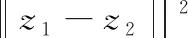
(11)

核特征空間較高的維度使得計算稀疏系數變得困難，因此通過降維方法來提高計算效率。在WKSRC中，可以使用KPCA來降低核心特征空間的維度。在KPCA中，如果設定降維后的特征空間維數為d，則變換矩陣B可以表示為B=[β1,…βj…βd]∈Rn×d；對于j=1,…,d，每個向量βj是對應于非零特征值的標準特征向量，通常選擇前d個最大特征值。通過變換矩陣B，上述問題可以表示如下

s.t.BTk(·,y)=BTKα

(12)

因此在原始特征空間中線性不可分的問題得以解決，樣本在高維特征空間中變得線性可分。在核特征空間中，使用降維方法來減小維度。與映射函數一樣，在線性降維方法中也可以用核技巧來獲得非線性數據。 核特征空間的非線性特征得以保留并用于解決分類問題。

2.2 局部結構信息

傳統的加權稀疏分類方法已經應用于人臉識別和在軸承故障診斷中，相比傳統的稀疏分類算法擁有更高的分類準確率。對于某些非線性信號，基于歐幾里得距離的加權稀疏分類方法往往不能獲得較好的分類效果

(16)

(17)

使用歐幾里得度量計算距離時，組間的距離會小于組內距離。利用最大間隔最小鄰居(LMNN)可以克服上述不足。

大間隔最近鄰[7](Large margin nearest neighbor)分類算法是統計學的一種機器學習算法。該距離度量方法充分利用先驗知識來從標記的樣本中學習馬哈拉諾比斯距離度量。通過訓練使得k最近鄰歸屬于同一類，而來自不同類的樣本以較大的余量分開。輸入空間的這種全局線性變換確保了同一類中的較小距離和不同類之間的較大距離。LMNN最初旨在提高K最近鄰(KNN)分類性能。從字面上理解，同一種類的輸入訓練集應該足夠接近；其次，不同種類的輸入訓練樣本應該足夠地分開。

基于上述理解，LMNN的損失函數由兩個項組成，一個用于將目標鄰居拉近，另一個用于將不同類別的樣本距離更遠。懲罰每個輸入與其最近鄰之間較大距離的項定義如下

(13)

懲罰不同類別樣本之間的距離的項被定義為

(14)

這里的yil=1，當且僅當yi=yl，yil=0；否則，xl表示來自xi的不同類別樣本。最后，結合上述兩項并定義一個損失函數如下，其中μ∈[0,1]是平衡上述兩項的權重參數

ε(L)=(1-μ)εpull(L)+ηεpush(L)

(15)

該種距離度量充分利用先驗知識使得k近鄰總是歸屬于同一類，而來自不同類別的樣本被大間隔分隔。輸入空間的這種全局線性變換確保了同一類中的較小距離以及不同類之間的較大距離。在本文中塊對角矩陣可以定義如下：

diag(W)=[dist(y,x1),…,dist(y,xn)]T

(18)

用馬氏距離來計算兩個向量之間的距離

(19)

其中M=LTL由LMNN得到。如果測試樣本y與訓練樣本xi之間的大距離Wi表明它們不太可能屬于同一類別，并且相應的αi往往很小，這也表明xi不能較好地表示y。在使用歐幾里得度量時，由于表示全局距離并且對噪聲敏感，所以如果y和xi實際上屬于不同的類別時y和xi之間的距離很小，則相應的αi往往很大，這會導致稀疏表示不準確。通過學習方法來測量距離。具體而言，訓練集包括相同類別樣本中的噪聲變化。在訓練詞組中，線性變換矩陣L可以學習這些模式。通過這種投影，輸出空間對不相關的噪音不敏感。因此，LMNN距離度量更可能呈現兩個信號之間的正確距離。

2.3 基于核空間稀疏表示的信號分類模型

本節提出的LMNN-WKSRC將局部適配矩陣應用于核函數空間中的L1最小化問題，得到了核函數空間中的加權L1最小化問題。求解系數向量的問題可以被表述為以下加權L1最小化問題：

(20)

(21)

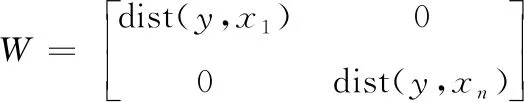
(22)

其中k(X,y)=[k(x1,y),…k(xn,y)]T∈Rn×1表示核空間內的核向量；K∈Rn×n表示相對應的核度量矩陣，其中Ki, j=k(xi,xj)。||Wα||1代指加權L1正則化項；dist(y,xi)表示每個原子與測試樣本之間的距離或相似度；λ控制表示誤差項||φ(y)-φ(X)α||2和加權正則化項間的權重。通過式(22)得到系數向量之后。將計算c類訓練樣本的重建誤差來確定測試樣本的標簽。與SRC和KSRC類似，除了與測試樣本所屬類別相關的部分外，系數向量將是稀疏的，大多數α的項為零

ri=||〗BTk(X,y)-BTKα||2

(23)

(24)

算法流程如表1所示。

表1 算法流程

3 驗證

本研究在軸承振動信號數據庫和航空發動機振動信號上對所提出的算法進行實驗驗證，實驗結果證明了該分類算法的有效性。為了充分驗證所提出的算法的分類效果，將WKSRC與3個現有的算法SRC，WSRC和KSRC在數據庫上進行比較。在KSRC和WKSRC中，需要將原始樣本映射進入高維內核空間。使用線性核作為非參數內核來獲取內核特征空間。然后，使用KPCA來減小特征維度降低系數向量的計算復雜度。在所有實驗中，使用SPAMS(SPAMS是用于解決涉及稀疏的機器學習和信號處理問題正則化的開源工具箱)軟件包來解決內核特征空間中的加權L1最小化問題。稀疏求解的系數λ的值取5，以保證非零系數不超過20個(共100組數據)。

采用西儲大學公開的軸承數據進行實驗驗證。表2所示為軸承故障類別。從圖1所示的振動幅值圖可以看出：即便注入損傷大小各異，但振動信號的振動模態卻相差無幾，比如0.84 cm的內滾道損傷與0.42 cm的外滾道損傷的振動模態極為相近，這給準確區分出故障類型增加了難度。對于上述每一種故障類型，從原始振動信號中采集并構造100組數據，每一組數據的維數均為2 048。將全部的1 200個樣本構造成一個2 048行1 200列的矩陣D，矩陣中的每一列都代一種故障

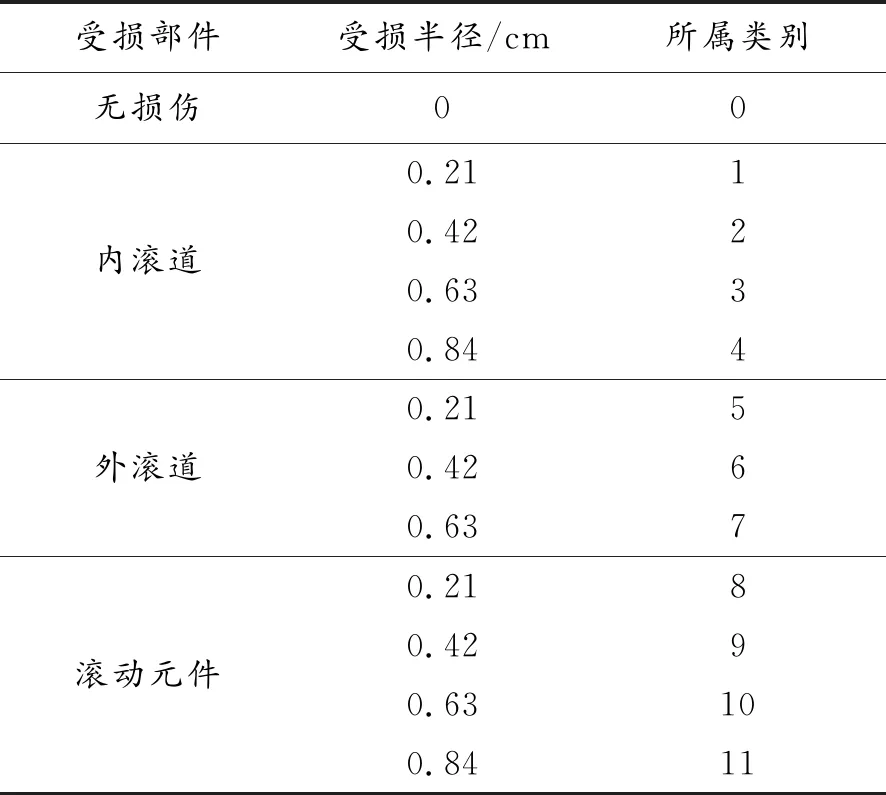
D=[D0,D1,…,D11] (25)

由于信號中不可避免存在噪聲干擾，因此第一步對數據進行中值濾波。提出矩陣每一列的多尺度熵和傅里葉系數作為特征來進行分類。接下來則對特征歸一化以防止某幾維數值過大或過小而影響分類準確率；本文采用通常的歸一化方法：

(26)

其中fij是第j個樣本特征向量的第i個特征值，歸一化之后的特征值區間為[ymin,ymax]。在特征歸一化過程中，采用與特征選擇相同的反饋機制確定歸一化的區間。相關實驗表明當歸一化區間為[-1,1]時，后續的故障診斷準確率最高。

每一組實驗均從100組樣本中隨機選出P組樣本作為訓練樣本，剩余樣本作為測試樣本。降維后的信號維數d分別取1 000和1 100。為了驗證本文算法的有效性。本文將所提出的算法與常見的稀疏分類算法進行識別率的對比；加權稀疏分類算法和核稀疏分類算法是本文算法在分類精度相對較高的兩種算法，本文同樣進行實驗對照；SVM是常用的分類算法，多數用于小子樣的分類。將上述實驗數據輸入到相應的算法中得到識別率折線圖2。

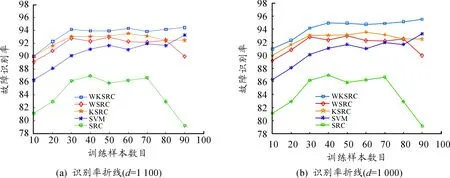
圖2 不同分類方法的故障識別率對比

4 結論

1) 本研究所提出的模型具有較高的故障識別率；當d=1 000時，平均識別率比單獨的稀疏分類算法高出將近9個百分點，比常用的支持向量機高出3個百分點；當d=1 100時，平均識別率比單獨的稀疏分類算法高出將近9.8個百分點，比常用的支持向量機高出3.8個百分點。

2) 振動信號的局部結構信號對振動信號故障分類有著重要的意義。由于WSRC將振動數據的局部結構信息與SRC結合起來，取得了比SRC更好地分類效果。

3) 核技巧根據軸承振動信號強烈非線性的特點將數據映射到高維核空間，提高了故障識別率。

4) 當對振動信號進行編碼時，在一個過完備字典上，對于相似振動信號SRC或KSRC會選擇相當一部分相同的基；而選擇LMNN方法作為信號之間的度量能夠更加準確地計算兩列信號信號之間的距離，從而獲得更高的故障識別率。