基于多普勒譜非廣延熵的海面目標檢測方法

陳世超 羅 豐* 胡 沖 聶學雅(西安電子科技大學雷達信號處理國家重點實驗室 西安 710071)(西南電子技術研究所 成都 610036)

1 引言

海雜波背景下的小目標檢測是雷達信號處理中較為復雜的問題之一，海雜波的存在嚴重限制了雷達對一些小目標如導航浮標、潛望鏡的檢測能力。對海上低速小目標而言，在時域其反射回波被強海雜波回波淹沒，特別是在高分辨低擦地角高海況情況下，海雜波的非高斯、非平穩性以及長時相關性更加明顯，其統計分布出現較長的拖尾，海尖峰效應突出使得虛警概率增加，傳統的基于統計模型的恒虛警(Constant False-Alarm Rate, CFAR)檢測算法不能起到很好的檢測效果[1,2]。

對海雷達回波會攜帶所照射純海雜波或含目標單元的多普勒信息，利用回波多普勒譜的聚集性可判斷海雜波背景下目標的存在與否。1948年，香農借鑒熱力學中的概念，最早提出香農熵用以描述信號或者數據的混亂程度[3]。對于海面小目標而言，目標的存在降低了海表面的混亂程度，因此可以用香農熵作為描述海雜波多普勒譜的集中程度的統計量。香農熵越小說明海雜波的多普勒譜越集中，目標存在的可能性越大。多普勒譜香農熵被廣泛引用于海面目標檢測[4—6]。其中，文獻[4]直接利用海雜波與目標的多普勒譜香農熵的差異來檢測目標，文獻[5]將相對多普勒譜熵作為一個特征，結合相對幅度與相對多普勒峰值，利用快速凸包學習算法實現海面漂浮小目標特征檢測。文獻[6]將多普勒譜香農熵和平穩小波變換相結合，提高雷達回波的信噪比的同時提高了海面小目標的檢測性能。

分形理論解釋了隨機信號中普遍存在的尺度不變性和自相似性，在雷達信號處理領域有著重要的應用。對于海面小目標而言，單一分形難以有效地區分海雜波與目標，由此研究人員相繼提出了一系列基于多重分形理論的海面目標檢測方法[7—17]。其中，文獻[11—14]研究了海雜波頻域和分數階Fourier變換(FRactional Fourier Transform, FRFT)域的多重分形特性，提出基于頻域分形Hurst指數以及基于FRFT域廣義Hurst指數的檢測算法。文獻[15—17]研究了海雜波時域的局部多重分形譜及多重分形(AutoRegressive, AR)譜，并將其運用于海面小目標檢測。但是描述分形特性時，通常需要雷達的觀測時間達到1 s甚至數秒，海面搜索雷達在實際使用時常常難以做到對每個區域進行長時間觀測，當觀測時間較短時，基于分形理論的檢測器的性能會有大幅度下降。

很多學者對非廣延熵描述非線性動力學系統進行了深入研究，證明非廣延熵能夠反映系統的非線性動力學特性[18—20]。本文結合海雜波頻譜的局部多重分形特性，對含目標單元與純雜波距離單元多普勒譜非廣延熵進行分析，論證了海雜波與目標的非廣延熵與多重分形特性間的關系，提出基于多普勒譜非廣延熵的海雜波背景下小目標檢測方法，最后通過IPIX實測數據驗證了目標和純雜波的多普勒譜非廣延熵較香農熵特征具有更強的對比度，同時采用非廣延熵特征描述海雜波多重分形特性，與頻域Hurst指數等特征相比，在觀測時間較短的情況下可以取得更好的檢測效果。

2 多普勒譜非廣延熵與多重分形

熵的概念由R.Clausius在1865年引入熱力學，一個多世紀以來得到了廣泛而成功的應用，成為統計物理學的基石[21]。1948年，香農借鑒熱力學中的概念，最早提出信息熵，即香農熵(Shannon Entropy, SE)用以描述信號或者數據的混亂程度，廣泛運用于信號處理領域中。SE定義為

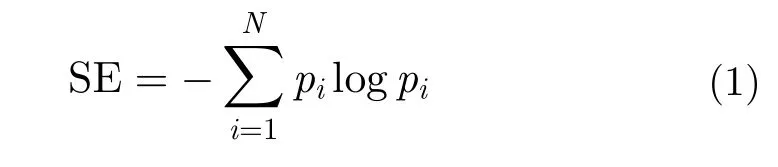
然而，香農熵是統計意義上描述系統整體性質的量值，并不能反映系統的具體狀態分布細節。因而香農熵無法體現分形、多重分形等反映海雜波非線性動力學本質的特性。由此，學者們又相繼引進了Kolmogorov熵，Renyi熵，非廣延熵等。

2.1 非廣延熵引入

2.2 非廣延熵與多重分形的關系

由此，將多重分形特性與多普勒譜聯合在一起，得到了用非廣延熵Sq(r)描述Dq(r)的表達式，因此Sq(r)可以描述海雜波系統的多重分形特性。

海雜波的頻域多重分形特性已被諸多學者加以證明，多重分形去波動趨勢分析法(MultiFractal Detrended Fluctuation Analysis, MF-DFA)是去波動分析法的一種推廣，它可對一組具有非平穩特性的序列在多個尺度下的多重分形特性進行更可靠的表示，可采用MF-DFA法對海雜波頻譜的多重分形特性進行分析和驗證[23]。參照MF-DFA計算步驟，可以得到不同q值下的波動函數。波動函數與MFDFA的階數q有關，不同階數的MF-DFA在去除序列趨勢方面的能力少有差異。對于求得的波動函數，查看波動函數Fq(s)與尺度s是否存在冪律關系，即

對式(11)兩邊分別取對數可得

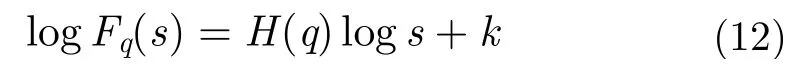
其中，k為常數。

因此，可在雙對數坐標系中對logFq(s)～logs進行最小二乘擬合，若它們存在線性關系，則該序列是分形的。同時，擬合的斜率即廣義Hurst指數H(q)。如果H(q)與q的變化無關，則判定該序列是單一分形的；如果H(q)是q的函數，則判定該序列是多重分形的。

3 基于多普勒譜非廣延熵的目標檢測方法

3.1 實測海雜波特性分析

本文采用的實驗數據來自加拿大McMaster大學的IPIX雷達數據庫網站，雷達頻率為9.39 GHz，脈沖重復頻率為1 kHz。各組數據包含同步收集的上述HH, VV, HV和VH 4種極化方式數據，所選數據的信雜比在—2～18 dB范圍內[24,25]，如圖1所示。每個數據文件含14個距離門的回波信號，目標主要占據1個距離單元，目標所在單元旁邊有2～3個影響單元，數據主要參數如表1所示。其表面包裹一層用來增強信號的鋁箔。目標漂浮在海面上，不斷上浮和下落。

3.1.1 多重分形特性分析

采用MF-DFA方法分析實測海雜波Doppler譜的多重分形特性。

3.1.2 多普勒譜特性分析

對海面目標而言，散射點之間相對靜止的成分較多，其多普勒譜往往較為集中。而無目標的純雜波單元，由于其粗糙及各散射點之間的雜亂運動特點，其多普勒譜顯得雜亂展寬。以數據文件#280為例，對目標所在單元(第8距離單元)與純海雜波單元(以第1距離單元為例)進行256點快速傅里葉變換(Fast Fourier Transform, FFT)，得到其多普勒譜如圖5所示。可以明顯看到含目標單元多普勒譜較純海雜波單元多普勒譜聚集性高。因為目標屬于錨定的，所以其頻點位于零頻附近。

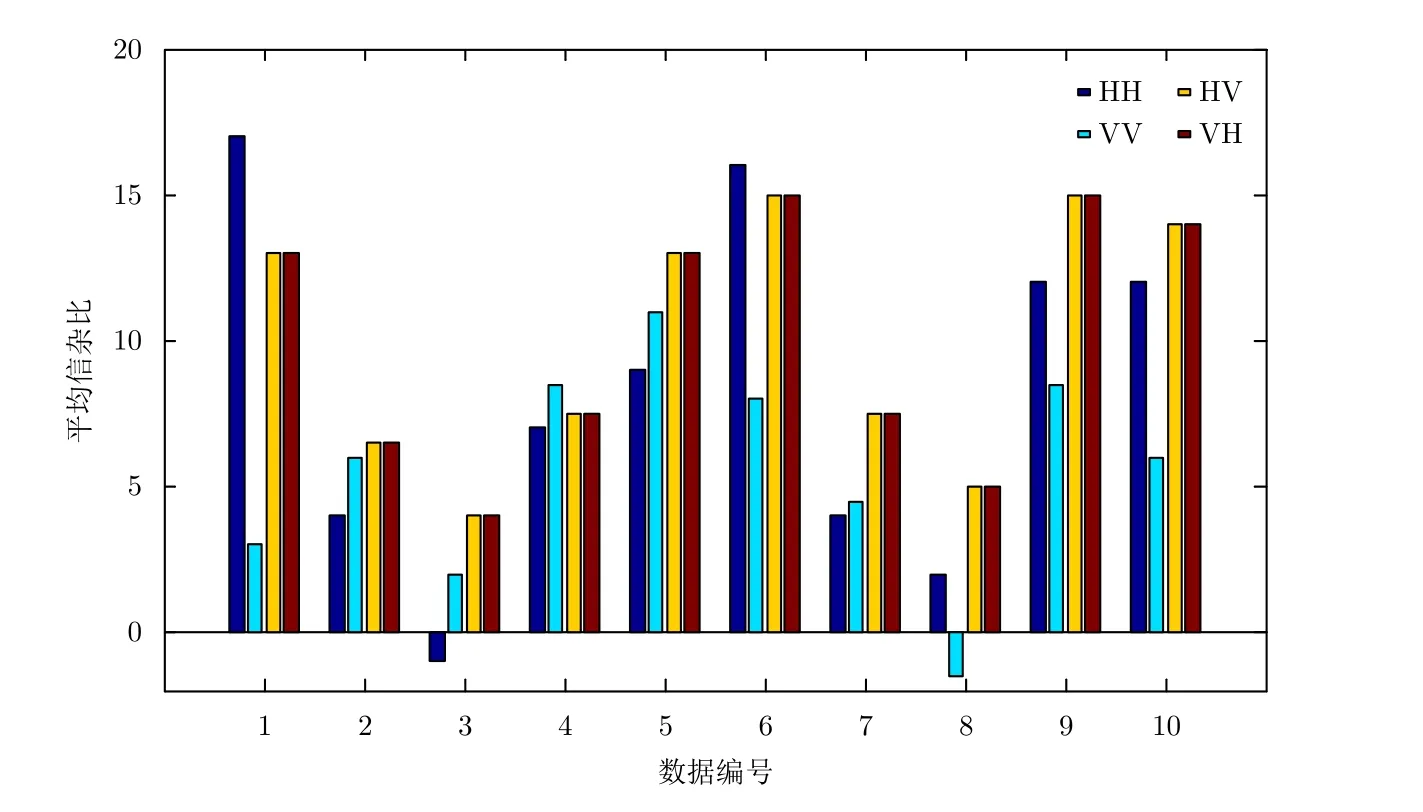
圖1 4種極化方式的平均信雜比Fig.1 The average SCR of four polarizations

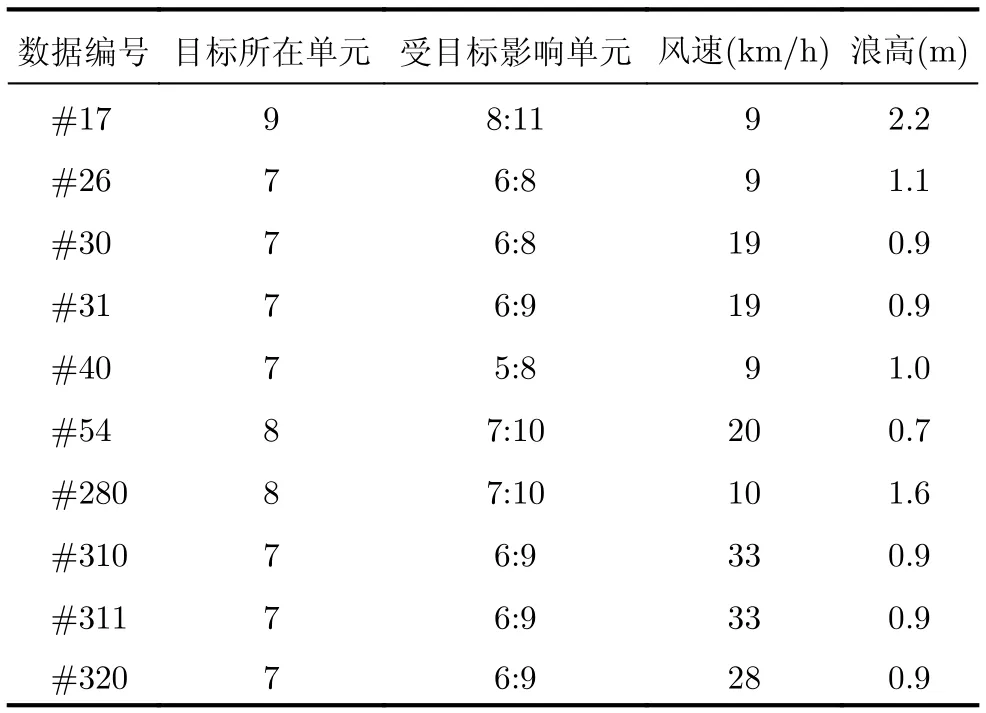
表1 1993年IPIX雷達數據主要參數說明Tab.1 Description of the data sets of IPIX radar database in 1993

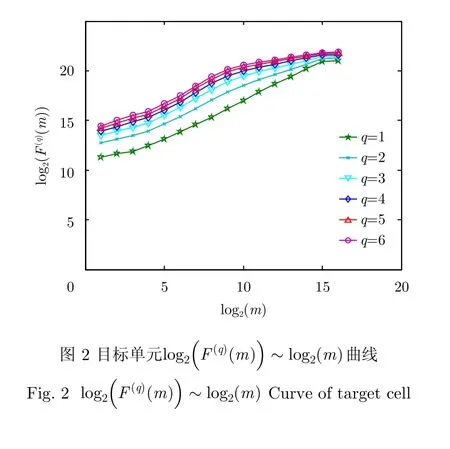
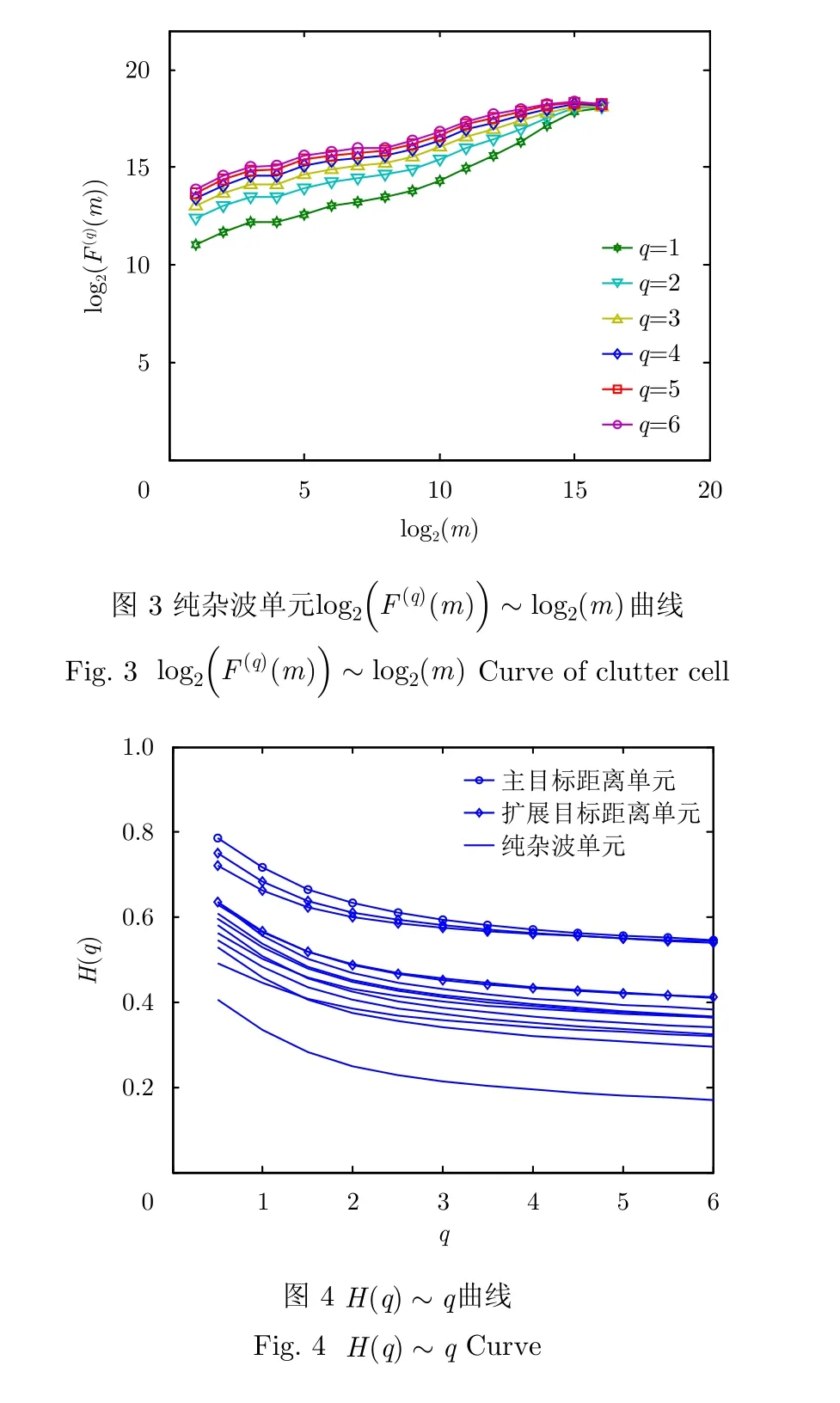
將每個距離單元的217個數據分割成512個數據長度256的數據序列，然后對每個序列進行FFT得到多普勒譜向量，按照式(5)分別計算其多普勒譜在不同值時的非廣延熵的平均值如表2所示，非廣延熵越小，多普勒譜越聚集，目標存在的可能性越大；非廣延熵越大，多普勒譜越分散，目標存在的可能性越小。由表2可以看出，含目標單元回波多普勒譜非廣延熵值在同一值下較純雜波單元低。由此可以采用多普勒譜非廣延熵進行目標檢測。

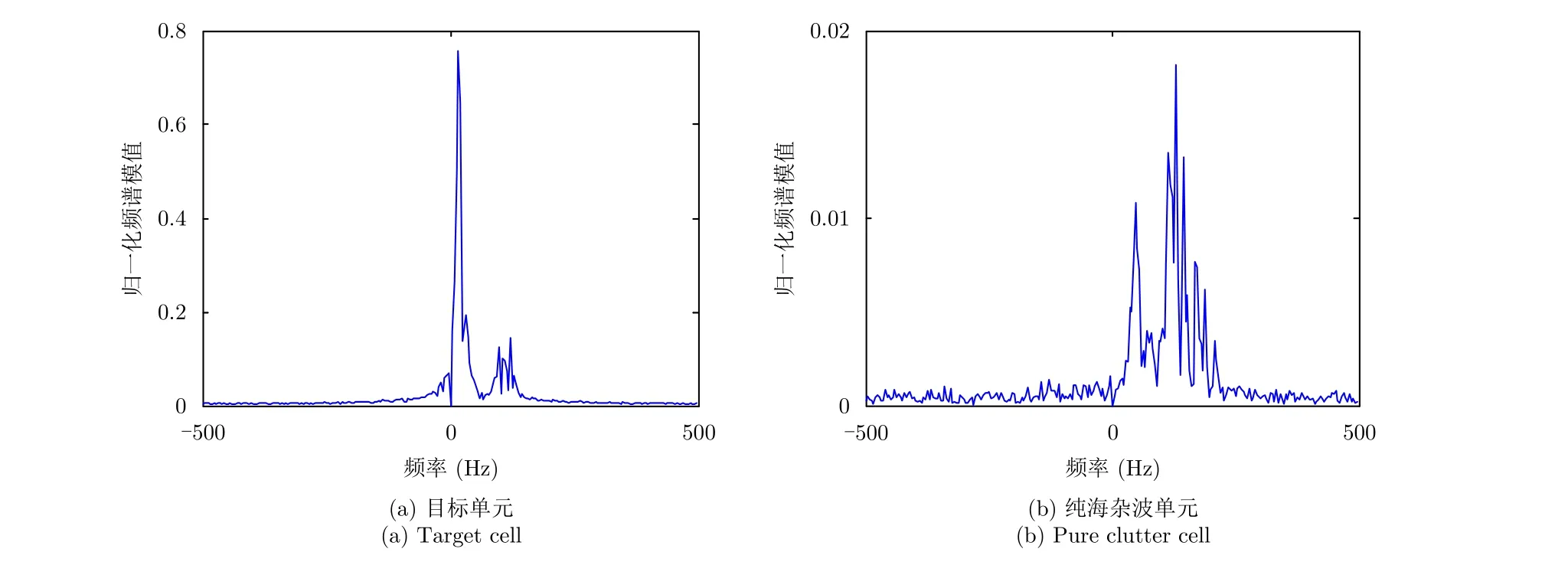
圖5 純海雜波Doppler譜與含目標Doppler譜比較Fig.5 Comparison of Doppler spectrums of target and pure clutter cell

為了加強聚集程度的對比，對上述結果進行立方操作以及和值歸一化，再進行非相參積累。圖6為相鄰16個脈沖積累后的歸一化非廣延熵值2維圖。可以明顯看出隨著值的增加，純雜波單元和目標所在單元的熵值對比度呈現上升趨勢。

為說明非廣延熵用于區分目標與雜波單元具有普適性，對1993年的10組IPIX數據的目標和雜波單元分別計算q= 2時的非廣延熵，取平均值得到統計直方圖如圖7所示。可以看出，不同極化方式下，對于不同信雜比的數據，目標單元和雜波單元的非廣延熵皆具有較好的可分性，且目標的非廣延熵值明顯小于雜波的非廣延熵值，可用于海面目標檢測。

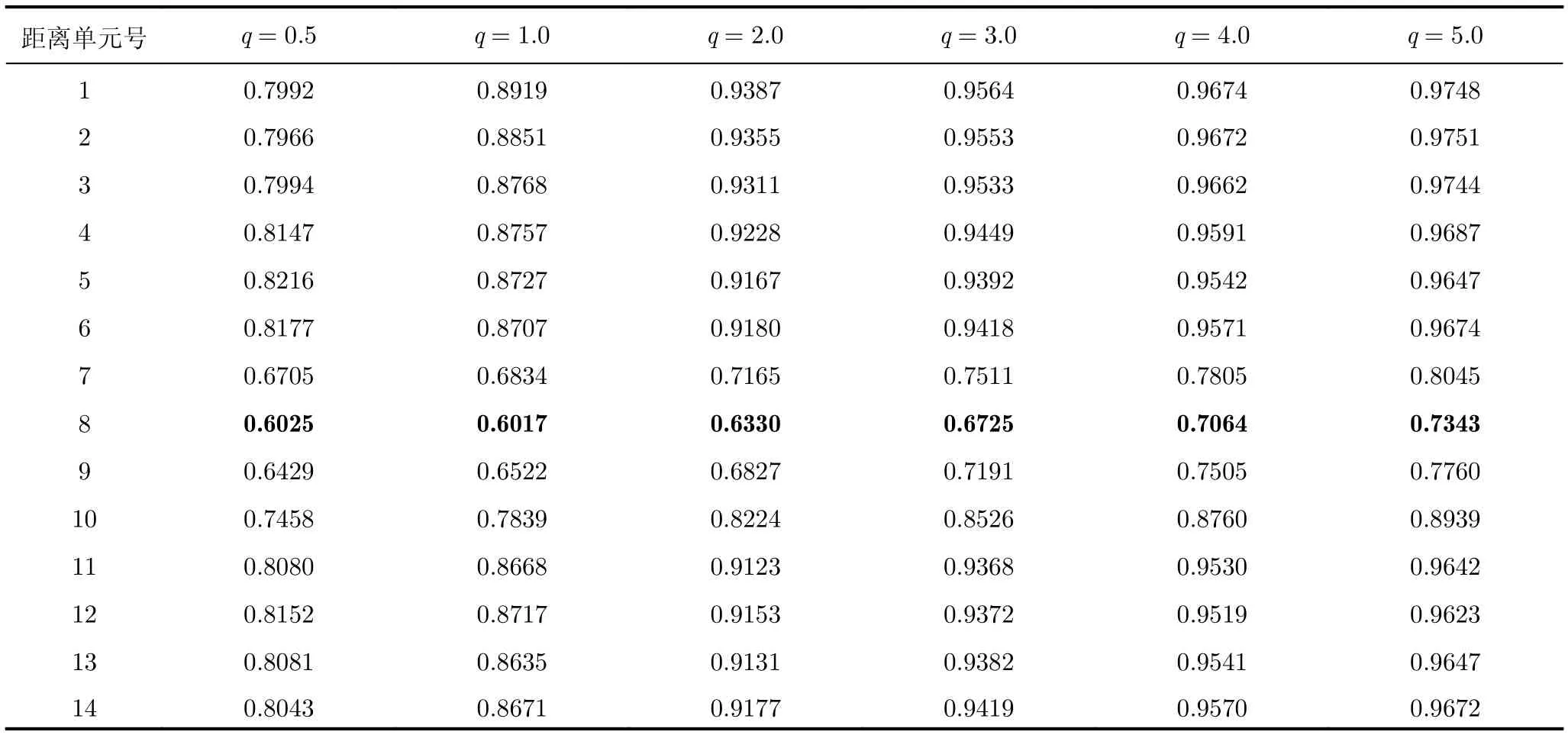
表2 全部單元多普勒譜非廣延熵值Tab.2 Tsallis entropy of Doppler spectrum of all the cells

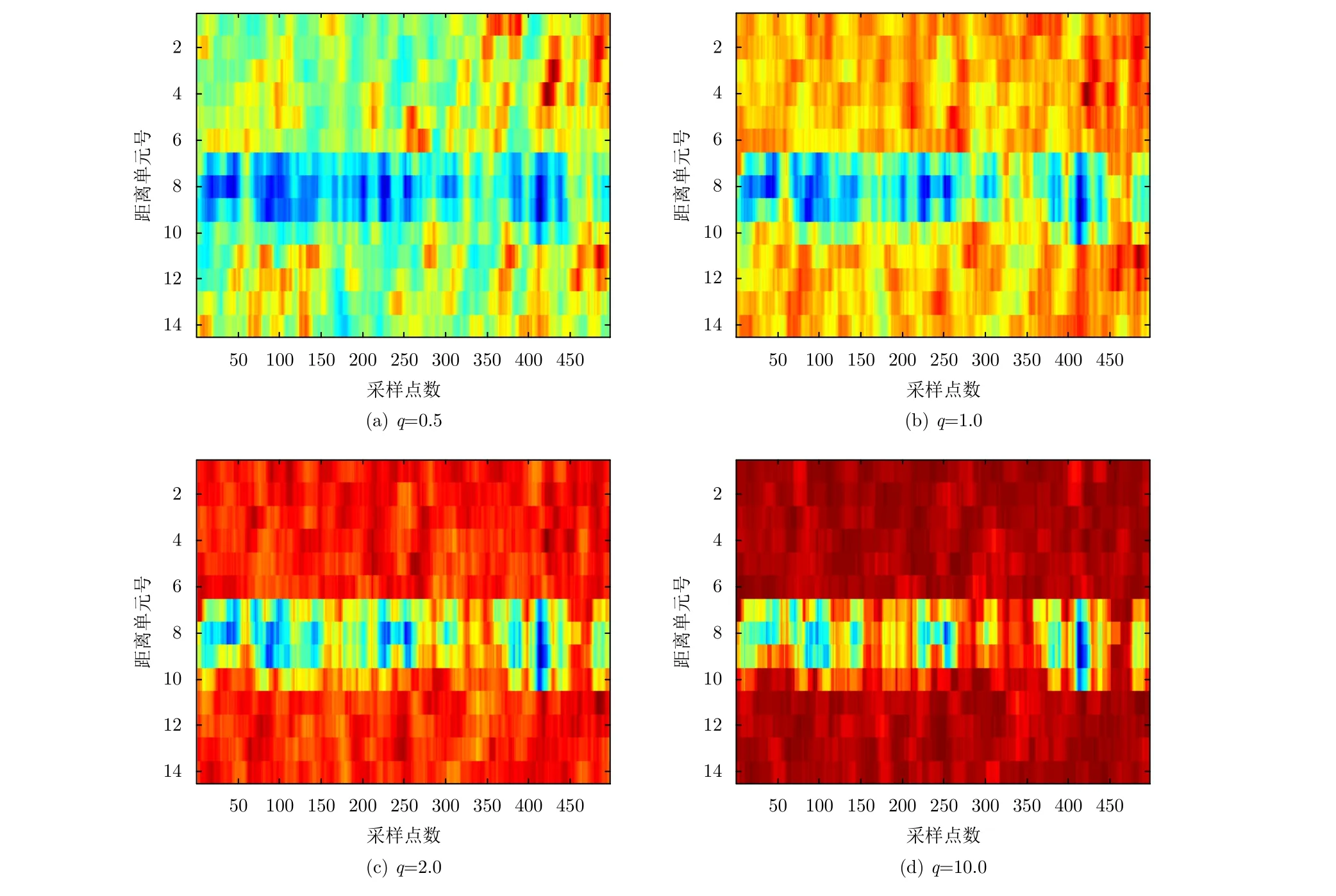
圖6 不同時的歸一化2維圖Fig.6 Normalized two-dimensional graphs of different values

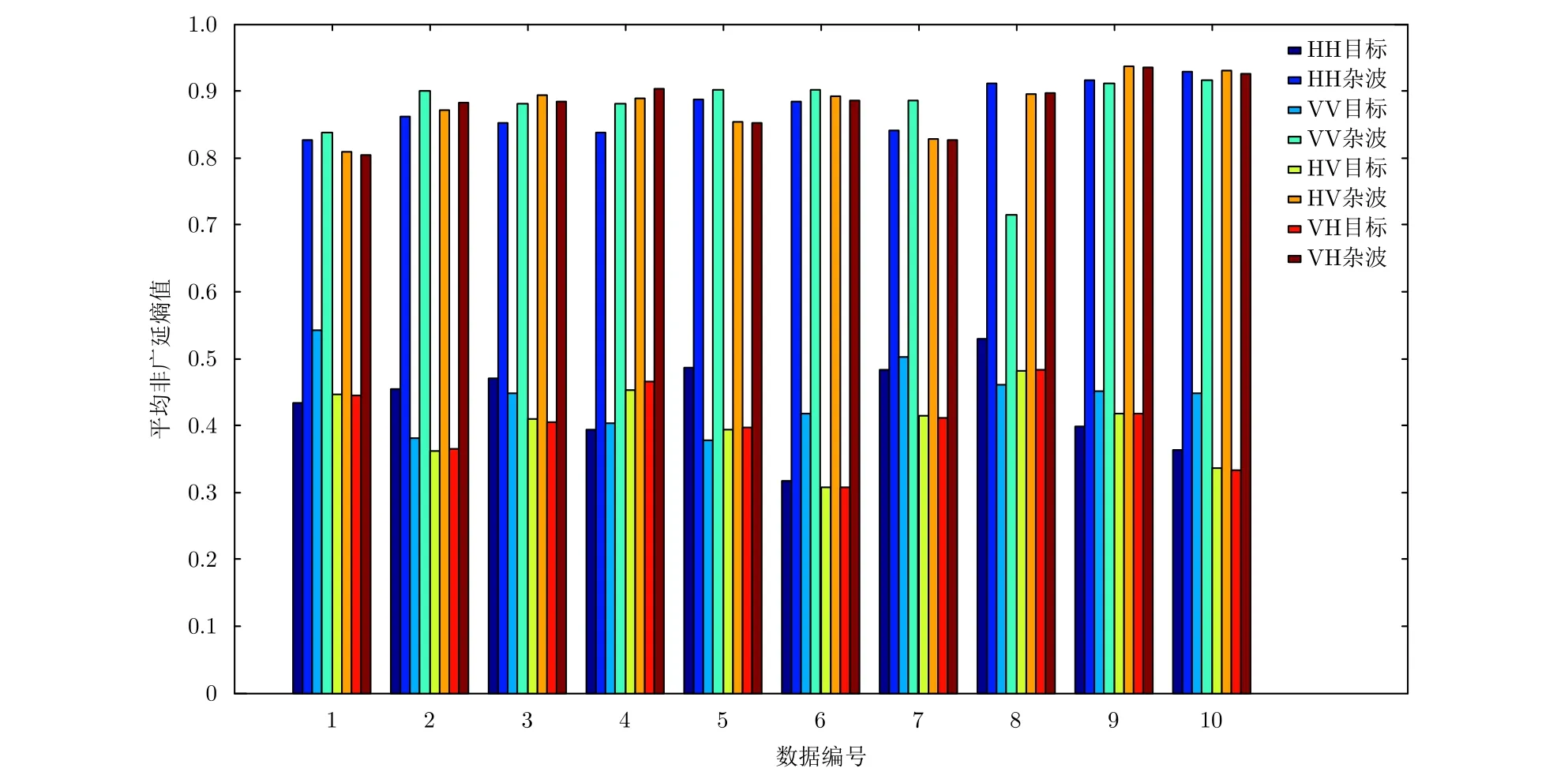
圖7 目標與雜波單元非廣延熵統計直方圖Fig.7 Histogram of Tsallis entropy of target cell and clutter cells

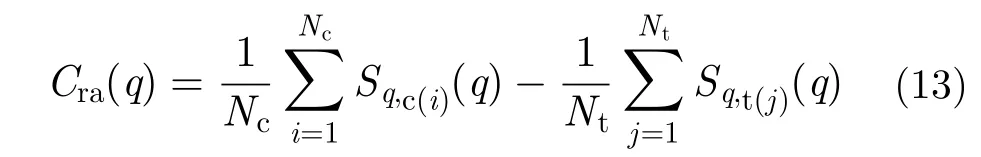
3.2 基于多普勒譜非廣延熵的目標檢測算法

雖然香農熵能很好地描述海雜波頻譜的聚集性，但其畢竟是一個統計意義上的檢測統計量，不能反映海雜波的非線性動力學特征。為了彌補這個缺點，采用能在一定程度上反映海雜波非線性動力學特性的非廣延熵描述頻譜的聚集性比采用僅能描述海雜波頻譜聚集性的香農熵更有優勢。本文提出基于多普勒譜非廣延熵的海面小目標檢測算法，主要流程如下：

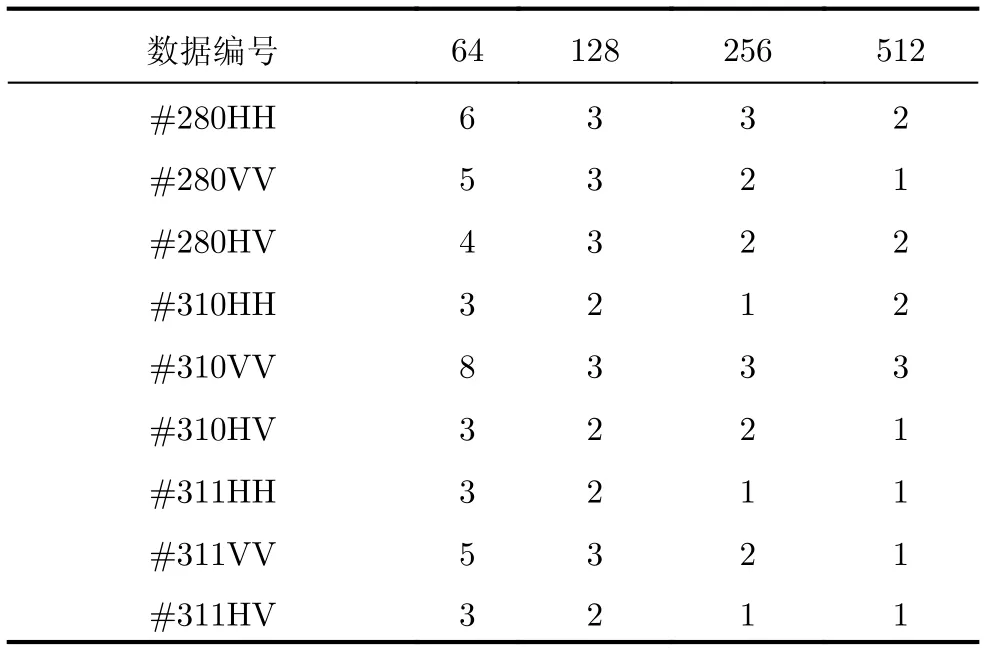
表3 不同FFT點數下最佳q值Tab.3 The best q values of different FFT points

步驟 3 針對有目標海雜波與無目標海雜波頻譜聚集性的不同，采用CA-CFAR方法設置檢測門限，熵值超過門限認為無目標，熵值小于門限認為有目標，即

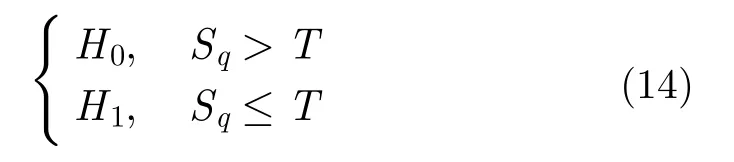
具體實現流程圖如圖8所示。

4 檢測性能分析

IPIX數據為低信雜比數據，大致范圍在—2～18 dB之間。為檢驗該方法的有效性，本文通過蒙特卡羅法計算不同值時的檢測概率，檢測概率和虛警概率由下式計算。

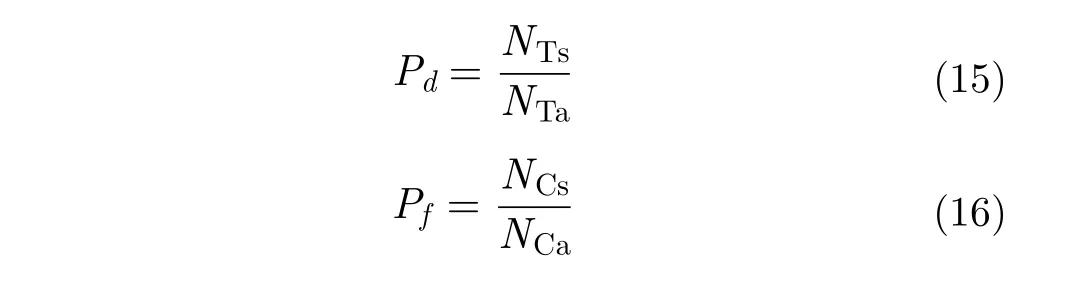
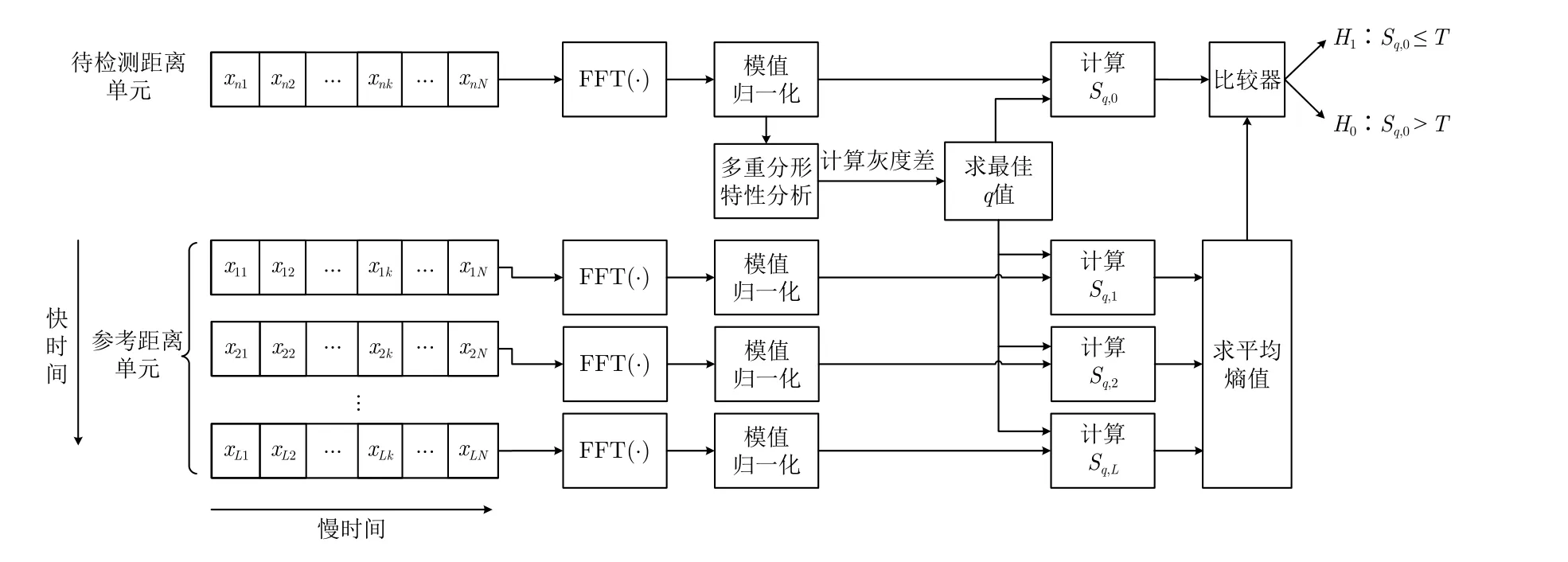
圖8 所提算法實現流程圖Fig.8 Flow chart of proposed algorithm

4.1 不同值下的算法的檢測性能

本文采用的IPIX雷達回波序列的長度為 217，由于雷達采樣率是1000 Hz，選取#280數據文件(不同極化方式下信雜比分布于3～8 dB)、數據文件#310(不同極化方式下信雜比分布于—2～5 dB)、數據文件#311(不同極化方式下信雜比分布于8～15 dB)，對其HH, VV和HV 3個通道的數據進行驗證。每一個數據文件長度為131072個采樣點，將其分為512個樣本，每個樣本觀測時間為0.256 s，按照所提算法流程計算不同虛警概率下算法的檢測概率，結果如表4所示。可以得出，當小于最佳值時，所提算法的檢測概率隨著值的增加而增加；當值大于最佳值時，隨著值的增加，檢測概率有所下降；當值較大時，如q=10時，檢測概率下降且此時運算量巨大。由此可以得出，在值選擇適當的情況下所提算法具有最佳檢測性能。對于不同信雜比數據，所提方法具有較好的檢測性能，信雜比越高，檢測效果越好。當選取觀測時間為0.256 s, FFT點數為256時，對于信雜比大于0 dB的數據，采用所提方法檢測概率可大于50%。

4.2 不同觀測時間下算法的檢測性能

頻域Hurst指數方法是海雜波背景下常用的基于多重分形特性的小目標檢測方法，在觀測時間較長，如序列長度為 213的情況下檢測概率通常可以高于80%，然而，隨著觀測時間的減少，該方法的檢測性能下降。選擇數據文件#280為本次實驗數據，取每個樣本的采樣點序列長度分別為 27, 28,29和210，則樣本數依次為1024, 512, 256和128。分別采用頻域Hurst指數法、基于香農熵的檢測方法和所提方法(取q=3)計算不同虛警概率下算法的檢測概率，結果如表5所示。可以得出，在虛警概率一定的情況下，隨著序列長度的增加，頻域Hurst指數法、基于香農熵的檢測方法和所提算法的檢測性能基本都呈現增長趨勢；在序列長度較短，即短時間觀測的情況下，頻域Hurst指數方法檢測性能下降嚴重，而所提算法具有最高的檢測性能。

對本文所提方法觀測時間的下邊界進行探索。選擇具有不同信雜比的數據#280, #310和#311，選取不同觀測時間采用所提方法進行實驗論證，結果如表6—表8所示。首先選取觀測時間為0.064 s，結果如表6所示。由表6可以看出，當觀測時間為0.064 s時，具有較低信雜比的#280和#310數據(低于10 dB)的檢測概率已有部分低于50%，而具有較高信雜比的#311數據(高于10 dB)的檢測概率全部高于50%；其次對低信雜比數據#280和#310，進一步提高觀測時間為0.128 s，結果如表7所示。由表7可以看出，當觀測時間為0.128 s時，檢測概率大多已大于50%；最后對高信雜比數據#311，進一步降低觀測時間為0.032 s，結果如表8所示。由表8可以看出，當觀測時間為0.032 s時，檢測概率多數已低于50%。

表4 不同值下算法的檢測概率(%)Tab.4 Detection probability of the proposed algorithm of different values (%)

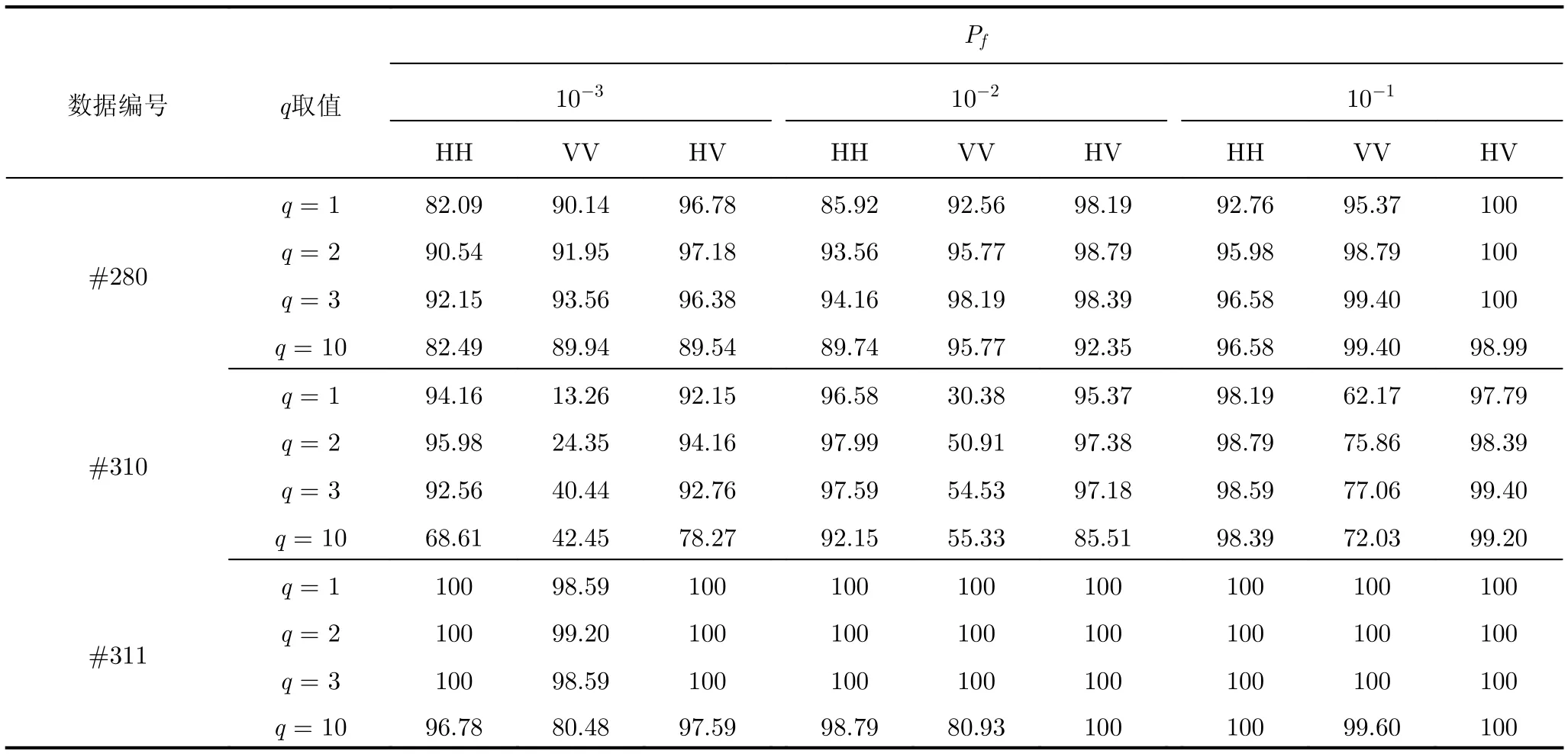
表4 不同值下算法的檢測概率(%)Tab.4 Detection probability of the proposed algorithm of different values (%)

images/BZ_75_225_2252_2258_2476.png#280 q = 1 82.09 90.14 96.78 85.92 92.56 98.19 92.76 95.37 100 q = 2 90.54 91.95 97.18 93.56 95.77 98.79 95.98 98.79 100 q = 3 92.15 93.56 96.38 94.16 98.19 98.39 96.58 99.40 100 q = 10 82.49 89.94 89.54 89.74 95.77 92.35 96.58 99.40 98.99#310 q = 1 94.16 13.26 92.15 96.58 30.38 95.37 98.19 62.17 97.79 q = 2 95.98 24.35 94.16 97.99 50.91 97.38 98.79 75.86 98.39 q = 3 92.56 40.44 92.76 97.59 54.53 97.18 98.59 77.06 99.40 q = 10 68.61 42.45 78.27 92.15 55.33 85.51 98.39 72.03 99.20#311 q = 1 100 98.59 100 100 100 100 100 100 100 q = 2 100 99.20 100 100 100 100 100 100 100 q = 3 100 98.59 100 100 100 100 100 100 100 q = 10 96.78 80.48 97.59 98.79 80.93 100 100 99.60 100

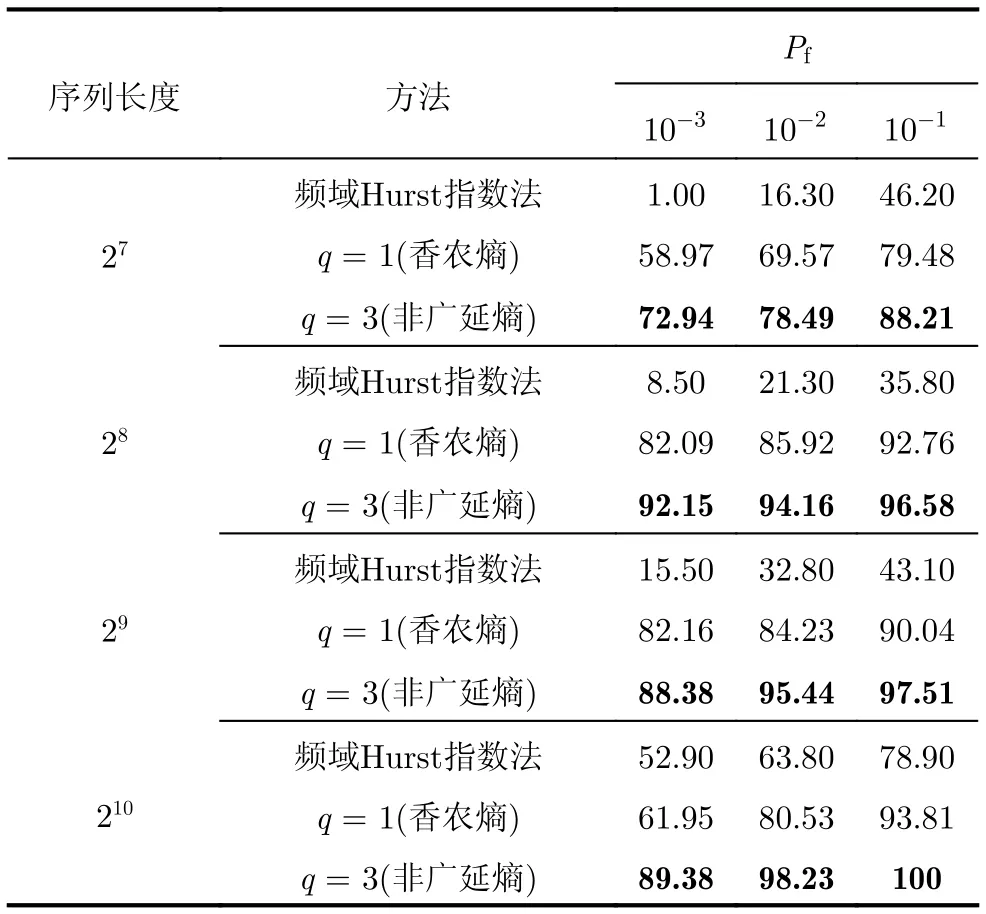
表5 3種算法的檢測概率(%)Tab.5 Detection probability of the three algorithms (%)

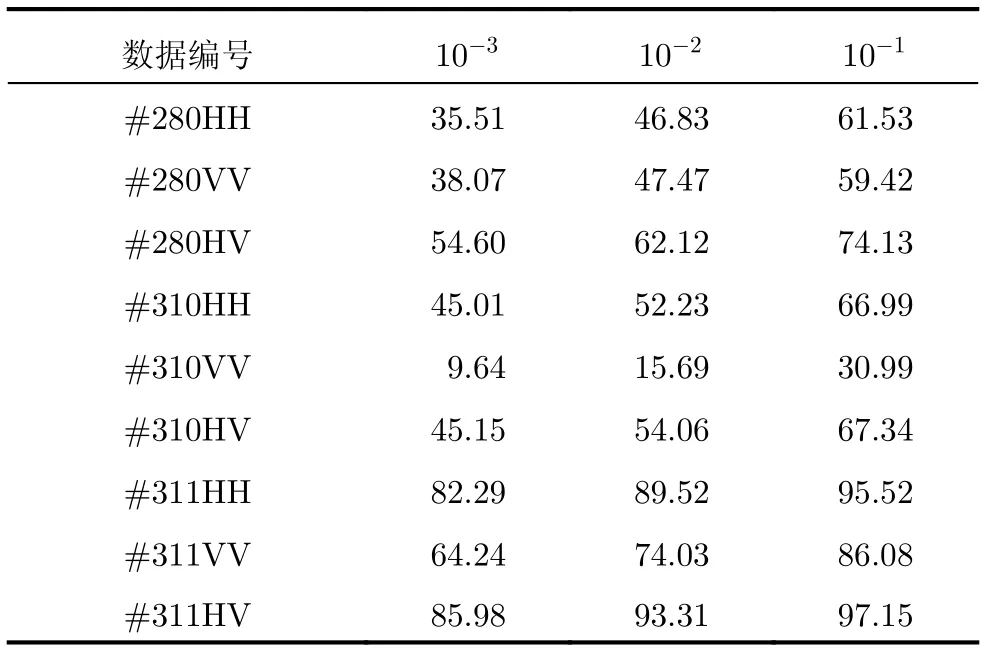
表6 觀測時間為0.064 s所提方法檢測概率(%)Tab.6 Detection probability when observation time is 0.064 s (%)

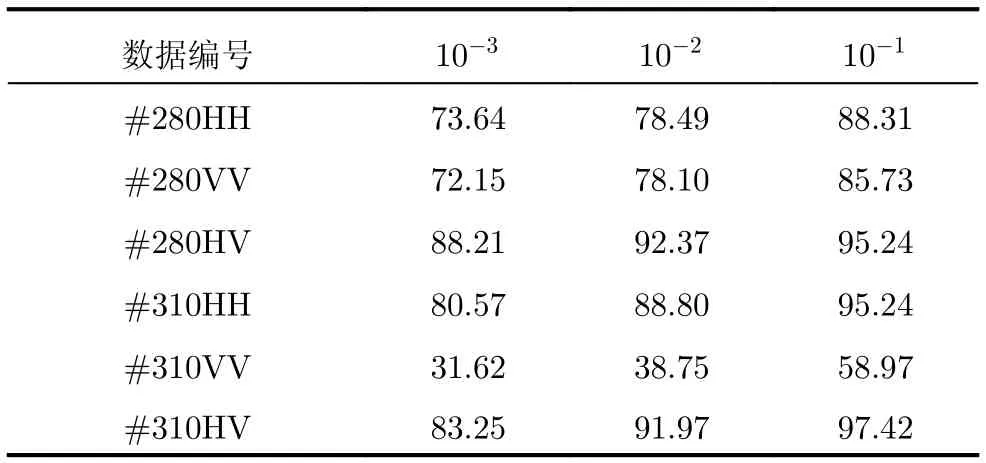
表7 觀測時間為0.128 s所提方法檢測概率(%)Tab.7 Detection probability when observation time is 0.128 s(%)

綜上所述，當觀測時間為0.064 s時，具有較低信雜比的數據(低于10 dB)檢測概率大多數低于50%，而較高信雜比數據(高于10 dB)大于50%。當觀測時間降低至0.032 s時，較高信雜比數據(高于10 dB)也降至50%以下。

表8 觀測時間為0.032 s所提方法檢測概率(%)Tab.8 Detection probability when observation time is 0.032 s (%)

5 結束語

本文通過對目標和純海雜波多普勒譜的聚集性和多重分形特性進行分析，提出了基于多普勒譜非廣延熵的海面小目標檢測方法。該算法綜合利用了海雜波的統計特性及非線性特性，解決了基于多重分形特性的檢測算法中需要長時間觀測的問題。最后利用實測數據將所提方法與現有的頻域Hurst指數法及基于香農熵的檢測方法進行對比，結果表明，本文方法具有較好的檢測性能。