面向海面目標檢測的陸海分離和海面分區算法研究

周 明 馬 亮 王 寧 楊予昊①(南京電子技術研究所 南京 210039)(中國電子科技集團公司智能感知技術重點實驗室 南京 210039)

1 引言

岸對海警戒雷達在國土安全防衛，如邊境控制、海面搜索、禁毒等發揮重要作用，然而強海雜波背景下的微弱目標檢測問題一直是岸對海警戒雷達的一大難題。在海面微弱目標檢測中，主要面臨兩個問題：(1)海島和陸地會導致成片或離散強雜波點，污染協方差矩陣估計的樣本；(2)復雜的海雜波特性制約了檢測器的檢測性能[1]。因此陸海分離和雜波分布擬合是海面目標檢測的研究重點。

雷達陸海分離方法主要可以分為基于先驗信息的海陸分離和基于圖像特征差異的海陸分離[2]。基于先驗信息的海陸分離借助高精度電子地圖、海岸線或港口背景圖像等實現陸海分離，當先驗信息缺失或不易獲取時，多采用基于圖像特征差異的海陸分離，如借助雷達回波圖、合成孔徑雷達(SAR)圖像或衛星圖等實現陸海識別。文獻[3]利用支持向量機和基于對象分類法對衛星圖像進行了海岸線提取，將結果與人工數字處理結果對比，表明兩種方法對海岸線提取具有亞像素精度。文獻[4]利用小波變換與主動輪廓法對SAR圖像進行海岸線提取。文獻[5]提出了一種基于從粗到細的層次結構水平集和窄帶水平集的海岸線提取法。文獻[6]利用圖像平滑、閾值分割和邊界跟蹤等技術對SAR圖像中的海岸線進行了提取，實現陸海分離。文獻[7]利用圖像的灰度和紋理對SAR圖像分割達到提取海岸線的目的，但由于定位精度不高和處理速度較慢，因而實用性不夠。

然而岸對海警戒雷達對海探測時通常無SAR圖像或衛星圖像輔助完成陸海分離，且隨著數據量的增大以及分辨率的提高，對陸海分離算法的速度提出了更高的要求，因此需要提出更準確更快速的陸海識別方法。

完成陸地和島礁樣本剔除后，需要對海雜波數據進行分布族辨識及海面目標檢測[8,9]。雷達利用相干脈沖進行目標檢測時，已有學者基于不同雜波模型分別提出廣義似然比檢驗(Generalized Likelihood Ratio Test, GLRT)檢測器[10]、自適應匹配濾波(Adaptive Matched Filter, AMF)檢測器[11]和自適應歸一化匹配濾波(Adaptive Normalized Matched Filter, ANMF)檢測器[12,13]，因此雜波數學模型是自適應檢測器推導的基礎，雜波分布模型的匹配度對檢測性能影響很大。

針對上述問題，本文提出一種面向海面目標檢測的陸海分離和海面分區算法。首先根據陸地回波序列間的相位具有強相關性，而海洋回波序列間的相位為隨機值這一特性，區分陸地雜波和海雜波；其次，考慮到雷達擦地角是影響海雜波模型的重要因素，本文提出了一種基于擦地角的海面分區算法，并根據分區結果，采用均方誤差檢驗法擬合出最優分布，進而選擇合適的檢測器進行自適應檢測；最后，通過對某S波段雷達實測數據進行分析，驗證本文所提出算法在海雜波下目標檢測的性能。

2 問題描述

海面目標檢測中，由于海雜波和目標通常可能處于相同多普勒通道，導致目標信雜比嚴重下降，給雷達目標檢測帶來很大難度。因此自適應檢測器(如圖1所示)逐漸成為海雜波下目標檢測的重要途徑，自適應檢測器通過估計參考樣本的頻譜特性，對待檢測單元進行雜波白化和目標積累來提高目標的信雜比，以改善檢測性能。

圖1 自適應檢測器檢測流程Fig.1 Adaptive detection process

自適應檢測器高度依賴于雜波向量的協方差矩陣。通常雜波的協方差矩陣是通過待檢單元周圍的距離單元作為訓練樣本估計得到的，并假設所選用的參考單元為純雜波單元，且滿足獨立同分布特征[14]。但實際對海目標檢測中，海島和陸地會引入成片或離散強雜波點，污染協方差矩陣估計的樣本，降低目標檢測性能，同時導致虛警率增加。此外，海雜波模型對于自適應檢測器的檢測器模型、檢測門限和檢測器性能優化具有重要作用，在常規的自適應檢測方法中，假設整片海面服從單一海雜波模型，可能出現所假設的雜波模型偏離真實雜波模型的問題，從而造成檢測性能下降。為改善上述問題，本文提出面向海面目標檢測的陸海分離和海面分區算法，算法流程圖如圖2所示。

3 面向海面目標檢測的陸海分離和海面分區算法

3.1 基于回波相位相關度的陸海分離算法

基于雷達回波的陸海識別算法主要是利用多普勒頻率、回波幅度、相位等信息區分海面和陸地。由于陸地回波的多普勒頻率主要位于零多普勒通道，而海雜波的多普勒頻率覆蓋較寬的范圍，因此通常利用多普勒特性區分陸地和海洋。但基于多普勒特性的陸海識別方法占用較多系統資源，為降低算法的計算復雜度，本文提出基于回波相位相關度的陸海識別算法。

假設雷達工作于機掃模式，在每個波位上發射脈沖數為K，基于回波相位相關度的陸海識別算法分為以下幾個步驟，首先提取出連續兩圈回波相同波位的相鄰脈沖的相位差，然后計算兩組相位差值的相關度，最后通過閾值處理算法得到陸海分割后的圖像。

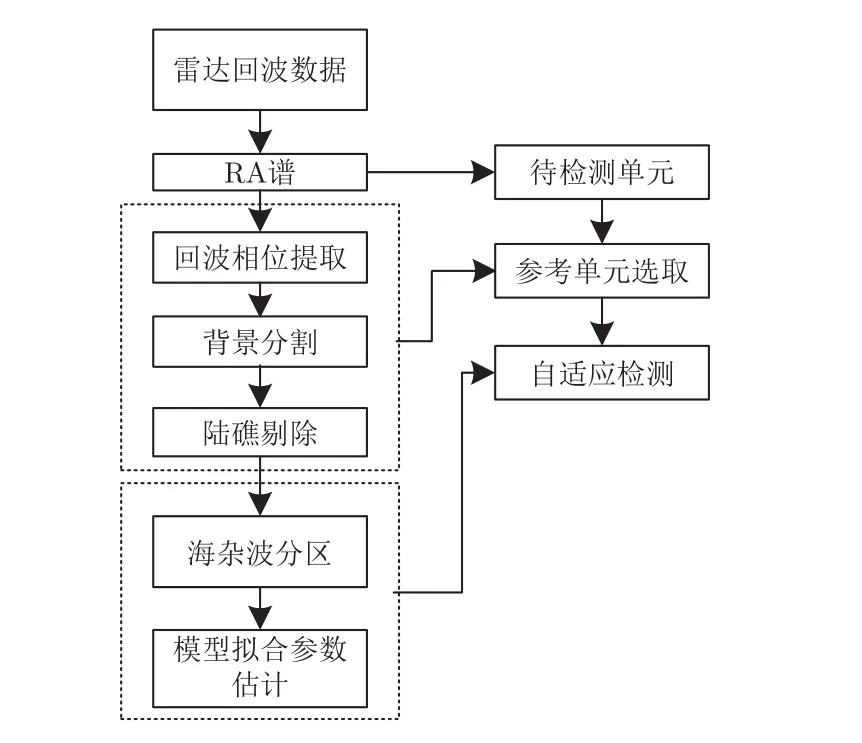
圖2 本文算法流程圖Fig.2 Flow chart of this paper algorithm

3.1.1 回波序列相位提取

3.1.2 回波相位相關度計算

回波相位相關度是通過計算連續兩圈回波數據中同一波位上相鄰脈沖的相位差的相關度得到。對于陸地回波，連續兩圈數據之間的相位相關度很高，而對于海洋雜波，由于海面是時變的，因此連續兩圈數據的相位之間的相關度很低，利用這一特性可以區分陸地區域和海洋區域。相鄰脈沖回波相位差k(m,n)定義為

3.1.3 閾值處理

計算所有分辨單元中的相位相關系數，量化到[0, 255]后得到一幅灰度圖像，稱為相位線性度圖像。對相位線性度圖像的背景分割可采用最大類間方差法(又叫做大津法)。大津法[15]是圖像學中一種自適應確定分割閾值的方法，將圖像按灰度級分為目標像元和背景像元，按照大津法原理自動求得的閾值對圖像進行二值化分割后，使得目標像元與背景像元的類間方差最大。本文將大津法推廣運用于陸海分離算法中，自動判定分割閾值，將相位線性度圖像進行二值化分割為陸地區域和海洋區域。大津法的基本過程如下：

假設相位線性度圖像灰度范圍為[0,L]，圖像的大小為M×N，陸地區域和海洋區域的分割閾值記作T，屬于陸地區域的像素點數占整幅圖像的比例記為w0，其平均灰度；屬于海洋區域占整幅圖像的比例為w1，其平均灰度為。圖像的總平均灰度記為，類間方差定義為

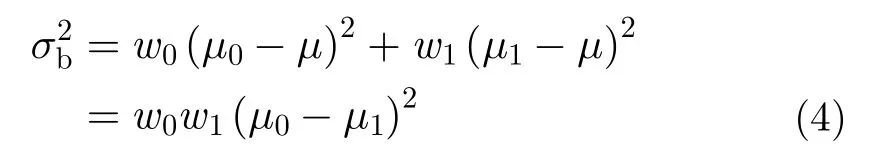
為避免出現邊界處模糊，分類不準確的現象，同時考慮兩類別內各像元的內聚性。定義類內方差為

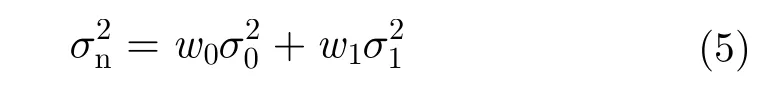
將回波相位相關系數映射到[0, 255]后，應用大津法計算得到分割閾值T，回波相位相關系數大于閾值處為海洋區域，反之為陸地區域。

3.1.4 算法可靠性分析

相位相關性區分陸海區域利用陸地回波序列間的相位具有強相關性，而海洋回波序列間的相位為隨機值這一特性，區分陸地雜波和海雜波。對于零多普勒的陸地區域，假設發送的線性調頻信號為

3.2 基于海面分區的自適應檢測技術

自適應檢測器中雜波分布模型的準確性對檢測性能影響很大。雷達檢測和信號處理中，常見的分布包括Rayleigh, Lognormal, Weibull和K分布等[8]。Rayleigh分布是最早應用的海雜波模型之一，其主要適用于中等或較高擦地角條件下低分辨率雷達海雜波的幅度分布建模，Lognormal分布適用于雜波變化較為劇烈，擦地角較小的場景，Weibull分布可以比較好的描述低海情、小擦地角雜波，K分布通常用于高分辨雷達的高海情、小擦地角的雜波建模中。圖3為某S波段雷達一圈數據作為擬合的數據輸入時，Rayleigh, Lognormal, Weibull和K分布的擬合結果。

采用均方誤差檢驗法衡量每個模型的擬合精度。均方誤差是實測概率密度與擬合的各分布模型概率密度的差平方的平均值

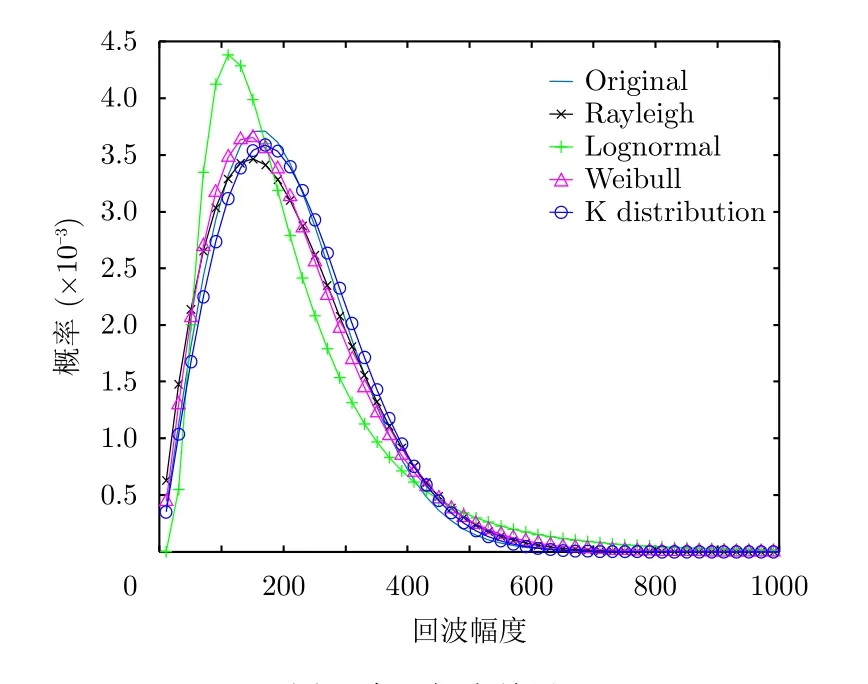
圖3 全局擬合結果Fig.3 Fitting result of radar data

從圖3可以看出，K分布具有更好的擬合性能，但將海雜波區域按距離相平均分為20份后重新擬合，擬合后的結果如表1所示。

表1 分塊后擬合結果Tab.1 Fitting result of uniformly partitioned data

從統計結果來看，由于海面真實狀況復雜，針對海面數據擬合時采用單一模型難以達到較好的擬合準確度，考慮到雷達擦地角是影響海雜波模型的重要因素，因此本文提出一種基于擦地角的海面分區算法，將海面劃分為多個區域后擬合，從而提高雜波模型的匹配度。

假設雷達部署在高度為H的山頂，第1個距離門距離雷達直線距離為R1，最后1個距離門距離雷達直線距離為R2，地球半徑為R0，第1個距離門和最后一個距離門的擦地角差為，具體位置如圖4所示。

圖4 雷達位置示意圖Fig.4 Radar position diagram

4 仿真分析

本文所采用的數據來自某S波段雷達，該雷達架設在海邊海拔183 m的山上，采集對應的實際起始距離R1為1.8 km，每個距離門長度37.5 m，雷達工作在機掃模式，每個波位發射脈沖數為8個。

圖5給出了基于回波相位相關度的陸海分離結果。圖5(a)給出了該雷達連續掃描兩圈的相同距離門和波位上的回波間的相位相關系數值的2維圖，將量化到[0, 255]后，應用大津法將其分割得到圖5(b)的二值圖像，其中白色區域為陸地區域，黑色區域為海雜波區域。在自適應檢測的樣本選擇中，將避免選擇白色區域中的樣本參與檢測，從而提高協方差矩陣估計的準確性。

得到純海雜波區域后，將海雜波區分割為若干區域后精細化檢測。圖6給出了本文所提出的基于擦地角的分割結果，從分割結果可以看出，距離雷達較近處分割較細，距離雷達較遠處分割較粗，由于近海處海雜波受海礁、船舶等影響較大，因而分割較細有利于得到更準確的雜波模型。

根據圖6分割后的結果，對分割后的每個區域擬合，采用均方誤差檢驗法得到10個分塊的最優擬合結果，具體擬合結果如表2所示。從表2可以看出，10個分塊均服從復合高斯分布，其中6塊服從Weibull分布，4塊服從K分布，這表明復合高斯分布模型具有較好的雜波擬合度。

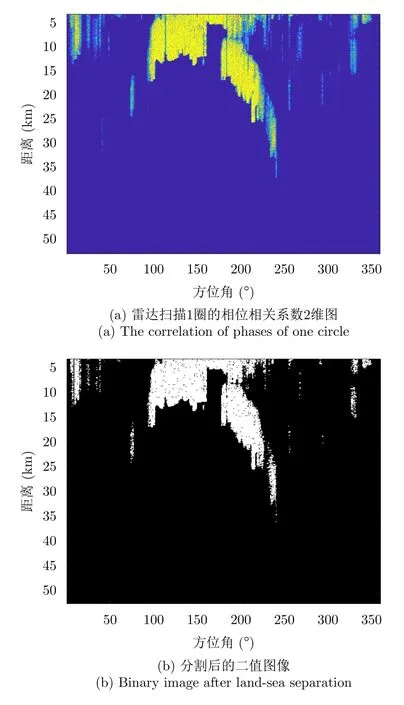
圖5 基于回波相位線性度的陸海分離結果Fig.5 Land-sea separation result based on the correlation of phases

圖6 基于擦地角的海面分區結果Fig.6 Sea surface zoning result according to the rubbing angle

最后通過蒙特卡洛仿真給出了所提出算法的海面目標檢測性能。在待檢測的分辨單元中加入給定信雜比和給定多普勒頻率的仿真目標信號，s(n)=aej(2nfd/fr+φ)，其中fd為多普勒頻率，位于區間[–fr/2,fr/2],fr為脈沖重復頻率，初相是區間[-,]上均勻分布的隨機變量，幅度參數Pclutter為仿真目標信號所加雜波單元N個脈沖的平均功率，SCR為信雜比。仿真中假設目標多普勒頻率fd=200 Hz，給定的目標虛警率Pf=10–4，此時目標的多普勒頻率接近海雜波譜的偏移量，即待檢測目標位于強雜波區。圖7(a)給出了位于島礁附近目標的檢測性能，仿真中在島礁附近隨機加入仿真目標，分別仿真了直接自適應檢測和剔除島礁樣本后自適應檢測的性能。圖7(b)給出了海面上隨機加入仿真目標時檢測性能對比，根據海面分區結果，在每個分區中隨機加入1個仿真目標，分別對比了直接自適應檢測和剔除島礁樣本后根據目標所在區域的雜波分布選擇合適自適應檢測器時的檢測性能。從圖7可以看出，兩種仿真場景下，隨著信雜比提升，目標的檢測概率逐步提升，采用本文提出的目標檢測算法，相對于傳統檢測算法性能提升比較明顯。

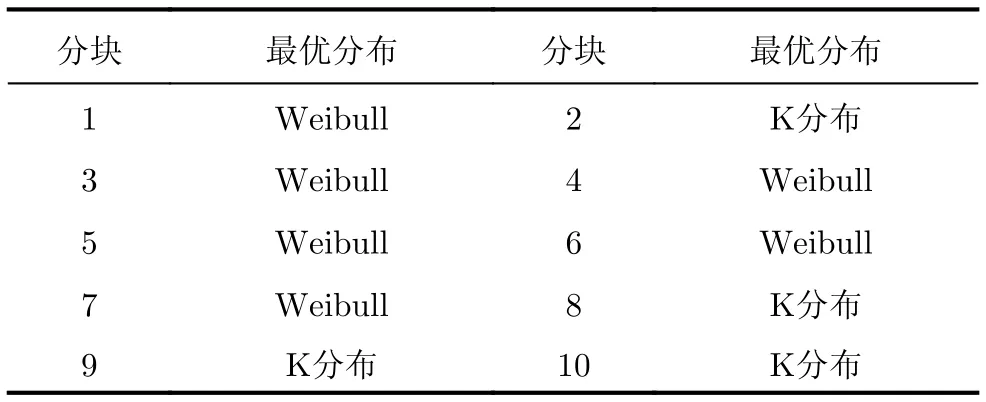
表2 雜波分區后的擬合結果Tab.2 Fitting results of partitioned data according to the rubbing angle

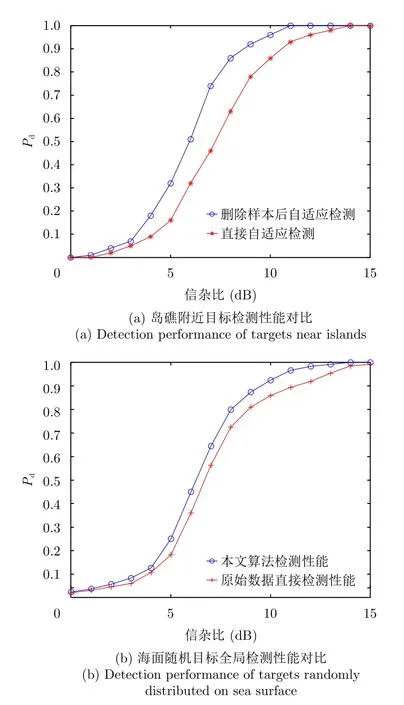
圖7 海面目標檢測性能Fig.7 Detection performance of targets on sea surface

5 結論

本文提出了一種面向海面目標檢測的陸海分離和海面分區算法。通過基于回波相位相關度的陸海分離算法和基于擦地角的海面分區算法，有效解決了自適應檢測中海島和陸地導致的成片或離散強雜波點污染協方差矩陣估計的樣本和自適應檢測中雜波模型匹配度不夠的問題。實測數據的分析與檢測結果表明，通過所提出的陸海分離算法和海面分區算法，目標檢測性能相對于傳統檢測算法性能提升比較明顯，從而驗證了本文的算法的有效性。