立足“平面向量基本定理”設計與求解相關問題

浙江省寧波市鎮海區駱駝中學 (315202)

丁林蓬

1.從參數含義的維度認識“平面向量基本定理”

筆者以為，這也是向量作為工具，表達平面的方式.對于這一維度內容的考察，筆者以為可以給出形如這樣的范例.

例1 如圖1，ΔABC中，AC=2AD.

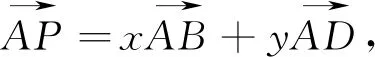
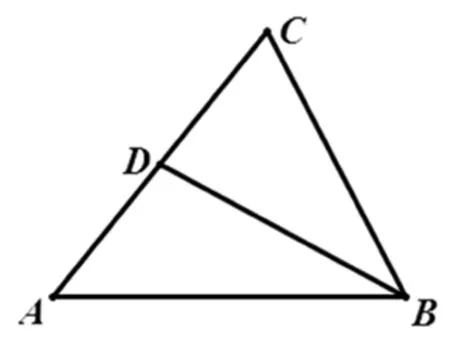
圖1

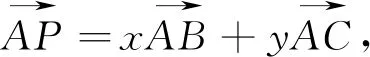
解析：形如(1)這樣的問題，多數情況是對于向量共線——“等和線”這一問題的考察.對于這個問題的解決可以借鑒三點共線的推論得到x+y=1.事實上，筆者設計這個問題，希望答題者認識到這一問題是以問題中的兩個向量構建坐標系，求解點P(x,y)軌跡方程的問題.

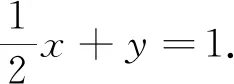
評析：理解平面向量基本定理中對應的參數的含義，對于從本質上統一這些問題具有指導意義.同時，也正是這樣的認知，為我們“化斜為直”提供了理論基礎，

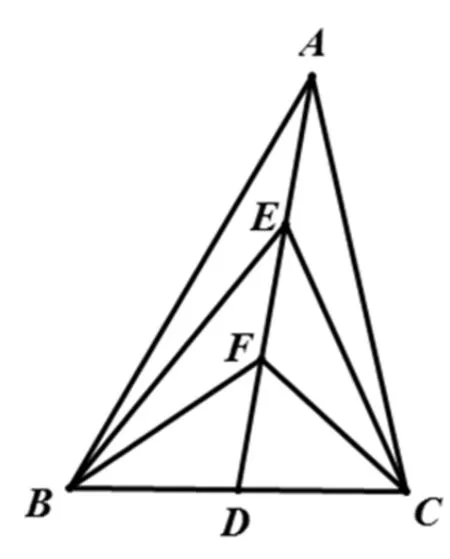
圖2

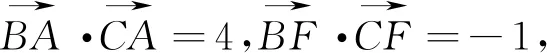
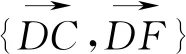
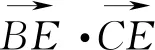
2.從模長的維度認識“平面向量基本定理”

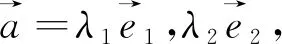
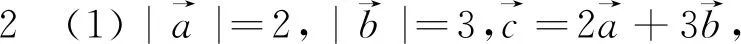
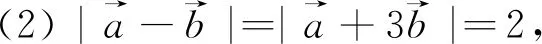
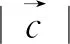
(2)的處理方式較多，這里給出兩種：

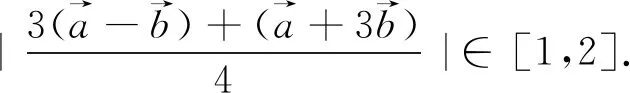
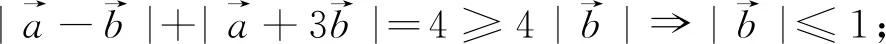
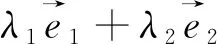
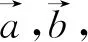
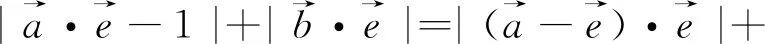
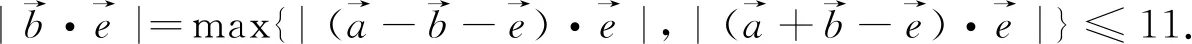
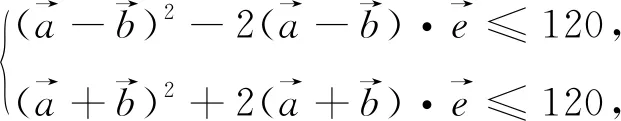
3.從向量代數性的角度認識“平面向量基本定理”

向量是既有大小，又具備方向的數學量.具有數字所有的一些良好屬性.利用這樣的數值屬性，我們可以設計并求解一些數學問題.

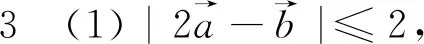
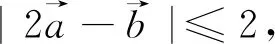
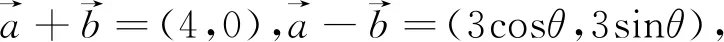
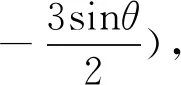
評析：這一組問題往往是學生面對的難點問題，同學們拿到問題之后往往會顯得束手無策，不知道思考的起點.事實上，以平面向量基本定理為載體，從向量代數性的角度出發往往能夠收獲向量問題在數值領域的本質屬性.

事實上，向量所具備的長度與角度兩個屬性是具有相同性的，同意數學問題可以從不同的兩個角度進行解決.這里給出一個問題，

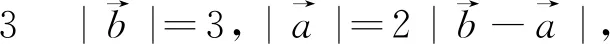
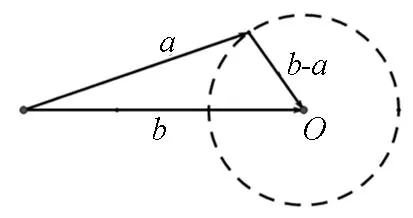
圖3

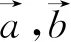
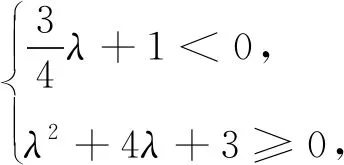
評析：從幾何的維度思考向量問題，往往能夠讓學生感到其中的巧妙.但是由于思考量較大，學生很難與教師之間產生共鳴.這不利于知識的傳授，以及對于該問題本質的探索.平面向量基本定理帶來的向量之間線性關系的前提下，適當的轉化為代數性運算，有助于幫助學生在高中階段形成數學學課“量”的統一.

4.反思

從多個維度對教材中最原始，最基礎的定理進行認識和重新分析，并以此為基礎涉及一些數學問題.既可以幫助學生全面的認識學習的新知識，又可以通過具體的例子促進新知識的內化.從而，在這樣的基礎上，不斷地培育學生的數學核心素養，使其分析、解決問題的能力在鍛煉中不斷提升.