從別證看一道奧賽題的條件多余

江蘇省姜堰中等專業學校 (225000)

陳 宇

第59屆IMO試題第1題設Γ為銳角⊿ABC的外接圓，點D,E分別在線段AB,AC上，滿足AD=AE，線段BD,CE的垂直平分線分別與圓Γ的劣弧AB,AC交于點F,G.證明：直線DE與FG平行(或重合).

圖1

筆者在此將部分借助三角法給出這道賽題的一個別證.同時論證該賽題一個G′條件“銳角⊿ABC”中的“銳角”為多余條件.

證明：按題意，分別連接AF,BF,DF;AG,CG,EG.設AB>AC，∠BAF=α,∠ABF=∠BDF=∠AGF=β,∠ACG=∠CEG=∠AFG=γ，∠CAG=δ(如圖1).則α+β=∠ACB,γ+δ=∠ABC.且銳角α,β,γ,δ滿足α<β，δ<γ<∠ABC.

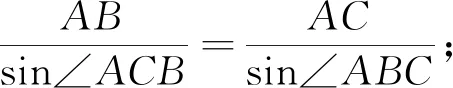
進而得β-α=γ-δ?α+γ=β+δ(∵β-α<∠AFG<∠ABC為銳角),又⊿AHK中,∠AHK=α+γ=β+δ=∠AKH,可知AH=AK,由此得DE∥HK.即DE∥FG.

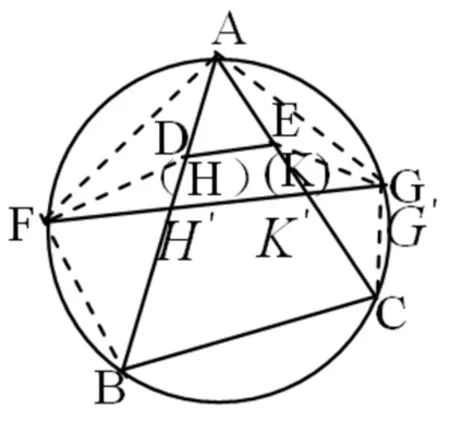
圖2

由AB>AC,當DE與FG重合時，圓Γ上的點C,G重合于C.進而點E,K,G,C重合于C.否則(如圖2),點E,K,C不重合于C，則CE﹥0，依題設條件，線段CE的中垂線交圓Γ于G′,必有FG′分別與AB,AC交于點H′,K′.由上述證明可知DE(FG)∥FG′.進而FG′與FG重合.

此時，在線段AB,AC上分別取AD=AE=AC(如圖3，點G,C重合于C.).連接并延長GD交圓Γ于點F.則∠ACF=∠ADC=∠BDF=∠DBF.

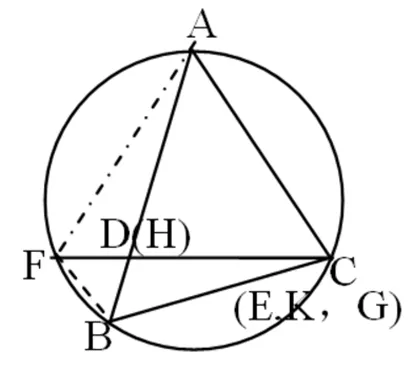
圖3

∴⊿BDF中,BF=DF.則點F在線段BD的中垂線上.此時DE與FG重合.

當AC>AB時,由對稱性可知，同樣有DE與FG重合.

當AB=AC時,有DE∥FG.若DE與FG重合.則點B,D,F;C,E,G分別重合.否則，如圖4，∠ADE=∠BDF=∠DBF=∠ACB>∠DBF.矛盾.

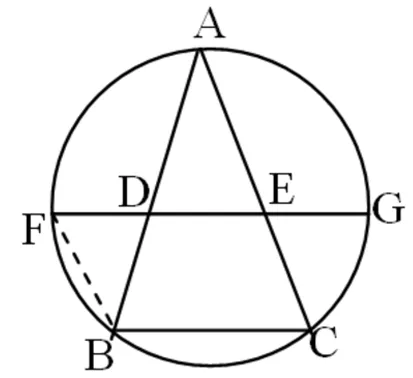
圖4

也許本文證明DE與FG重合的過程較煩.但參考答案中并未對DE與FG重合時相關點的位置關系給出證明.只是籠統的一句“結論得證”.似有遺漏之嫌.

參考答案從平幾角度證明，確實涉及到∠BAC的大小.但由本文上述證明知，在題設條件下，該試題結論成立，與∠BAC的大小無關，只與∠BAC的邊AB與AC的大小相關.即滿足0<∠BAC<π，原賽題結論總成立.DE與FG重合時，其重合的位置也只與∠BAC的邊AB與AC的大小相關.

進而，當0<∠ACB<π時，點D,E分別在線段AB,AC上，滿足AD=AE，線段BD,CE的垂直平分線分別與∠ACB，∠ABC所對的弧AB,AC交于點F,G(此處條件敘述與原賽題對應條件敘述同義，雖顯直白，但適用于任意三角形).結論成立.

可見，對于任意⊿ABC，在題設條件下，該試題結論成立.顯然，題設條件“銳角⊿ABC”中的“銳角”實為多余.

至此，該試題只需表為設Γ為⊿ABC的外接圓，點D,E分別在線段AB,AC上，滿足AD=AE，線段BD,CE的垂直平分線分別與∠ACB，∠ABC所對的弧AB,弧AC交于點F,G.證明：直線DE與FG平行(或重合).

其證明過程統一包含于上述別證(直線DE與FG平行(或重合))