基于演化搜索算法的助推器再入飛行模態分析

張意國，趙長見，趙俊鋒，賈生偉

（中國運載火箭技術研究院，北京，100076）

0 引 言

對于大部分運載火箭和彈道導彈而言，助推器工作結束后需要進行分離并被拋掉以降低結構重量。對于一般飛行器而言，在子級助推器分離時刻飛行速度不足以達到第一宇宙速度，使得分離后的助推器在地球引力的作用下將落入地球表面。助推器再入過程由于沒有主動控制力的作用，在重力及非線性氣動力的作用下將出現復雜的姿態運動。對于助推器再入姿態運動模態（即無控狀態下姿態周期性運動規律）[1]進行預示，有助于對助推器回收系統進行設計，同時也有助于發射場安控工作的組織實施。王景國等[2]人采用了傳統的基于3DOF模型的落點預測方法對火箭整流罩的殘骸落點進行估計，其中通過大量的試驗數據進行聚類分析結合工程經驗對阻力系數和參考面積這兩個關鍵彈道參數進行了計算。陳彬[3]等人對助推器再入運動的單通道運動特性進行了分析，分析了助推器再入過程姿態運動的穩定性。

為全面準確地描述助推器再入自由運動過程的姿態運動特性，有必要開展其三通道運動模態的研究。對助推器三通道運動模態的研究建立在助推器再入三通道耦合非線性模型的基礎上，相較于單通道線性化模型[3]，三通道運動學模型能夠提供更高的模型精度，同時也存在不止一組平衡點，對助推器再入動力學特性的描述可以更準確。但也因為非線性模型強耦合以及強非線性的特點，使得基于小擾動理論的線性系統理論對一些系統特性無法展開準確地分析。

本文采用了基于演化搜索算法的改進郭濤算法，解決高階、強耦合非線性動力學模型的多平衡點求解問題[4～7]，并在此基礎上對助推器再入過程平衡點的穩定性及演變規律進行了分析。

1 助推器再入非線性模型

在再入彈頭和自旋穩定飛行器動力學的研究中，常使用基于經典歐拉角描述的運動學模型，以便于更好地描述大姿態角運動下的運動規律[8,9]。對于再入助推器而言，其存在大范圍的姿態角運動，且姿態角運動存在高動態特性，適合于使用基于經典歐拉角及其角速度描述的姿態動力學模型來進行動力學分析工作。

經典歐拉角的定義如圖1所示，包括進動角、章動角及自旋角，是描述助推器體坐標系與準速度坐標系之間轉換關系的一組歐拉角，相應坐標系描述如下：

a）助推器體坐標系（Oxbybzb）。

坐標系原點O位于質心，O xb軸沿助推器縱軸向前為正，Oyb在對稱平面內指向上為正，Ozb軸與其余兩軸滿足右手定則。

b）準速度坐標系（Ox5y5z5）。

坐標系原點O位于質心，O x5軸沿速度方向向前為正，O y5位于包含Ox5的豎直平面內向上為正，O z5軸與其余兩軸滿足右手定則。

由準速度系轉到助推器體坐標系為1-3-1轉序：首先Ox5y5z5坐標系沿Ox5旋轉ζ（進動角）至Ox5y' z'坐標系；然后繞Oz'軸旋轉δ（章動角）至Oxby'' z'坐標系；最后繞Oxb軸旋轉λ（自轉角）至Oxbybzb坐標系。

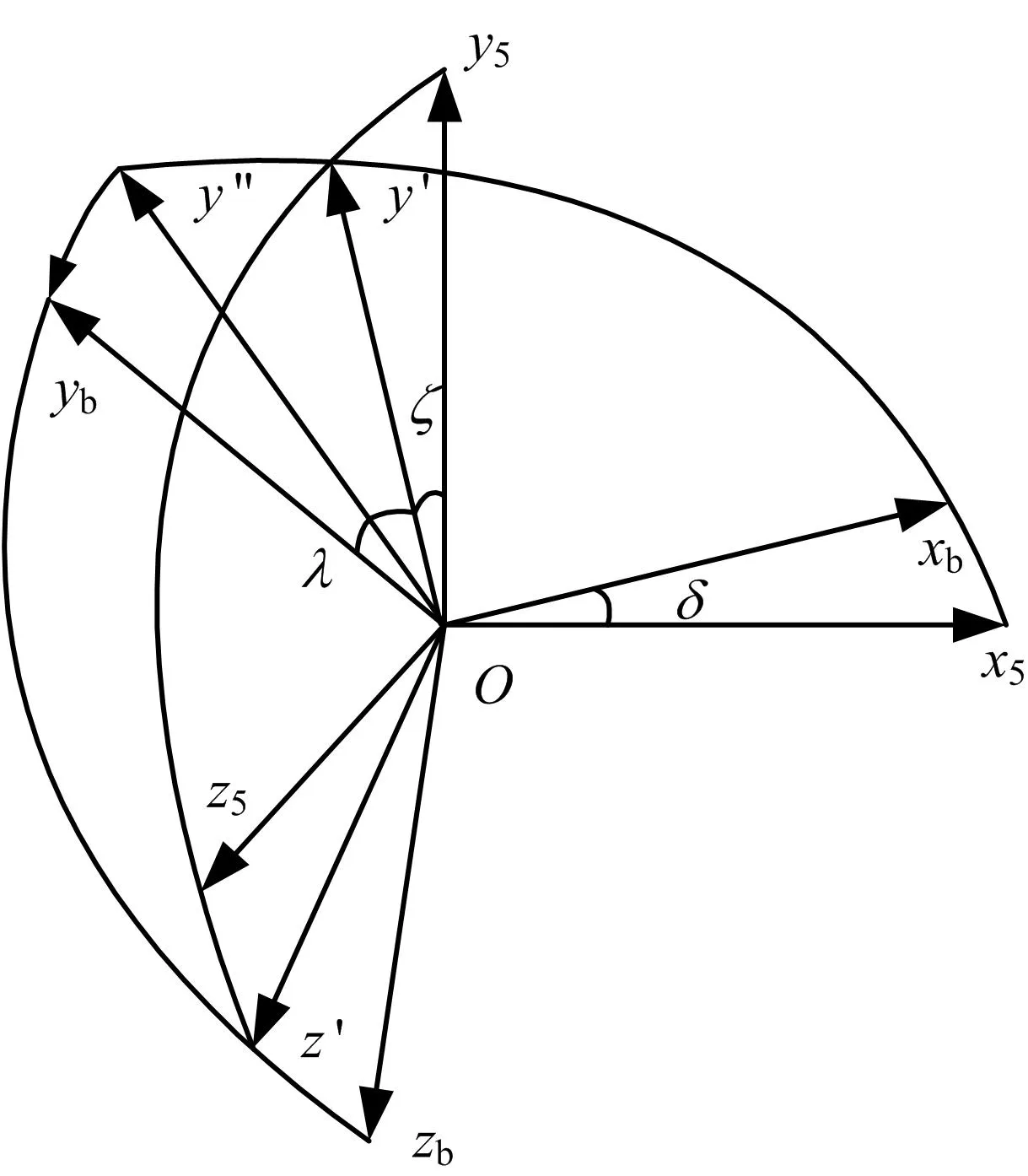
圖1 經典歐拉角定義Fig.1 Classical Euler Angle Definitionζ—進動角；δ—章動角；λ—自轉角

助推器再入飛行過程沒有控制力，只在重力和氣動力的作用下自由運動，而空氣動力一般在彈體系下描述，是與攻角α及側滑角β相關的變量，根據坐標轉換關系可得到α，β以ζ，δ，λ表示的表達式：

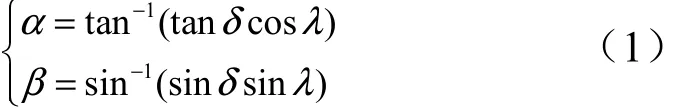
考慮到助推器姿態運動相對質心運動為快時變運動，在分析姿態運動時可以認為助推器速度的大小及方向保持不變，準速度系可視為慣性坐標系，則再入助推器的角速度（xω，yω，zω）可以用δ、ζ及λ的角速度之和表示：

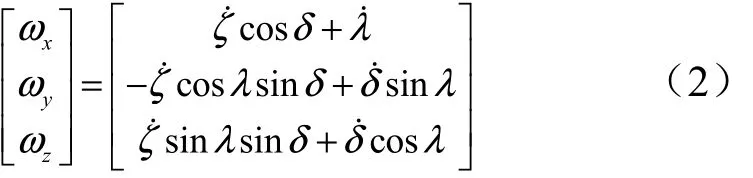
式中xω，yω，zω為彈體系下歐拉角的3個分量；ζ˙為進動角速度；λ˙為自旋角速度；δ˙為進動角速度。

對式（2）進行求導并進行轉換，可以得到以歐拉角表示的助推器非線性動力學模型：

式中xω˙，yω˙，zω˙為彈體系下歐拉角速度bω˙的3個分量；δ˙˙為進動角加速度；ζ˙˙為章動角加速度；λ˙˙為自旋角加速度。

可根據歐拉方程求得，矢量形式為

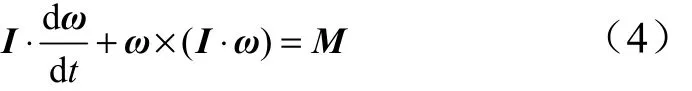
式中 I為彈體轉動慣量矢量；ω為彈體角速度矢量；M為合外力矩矢量。

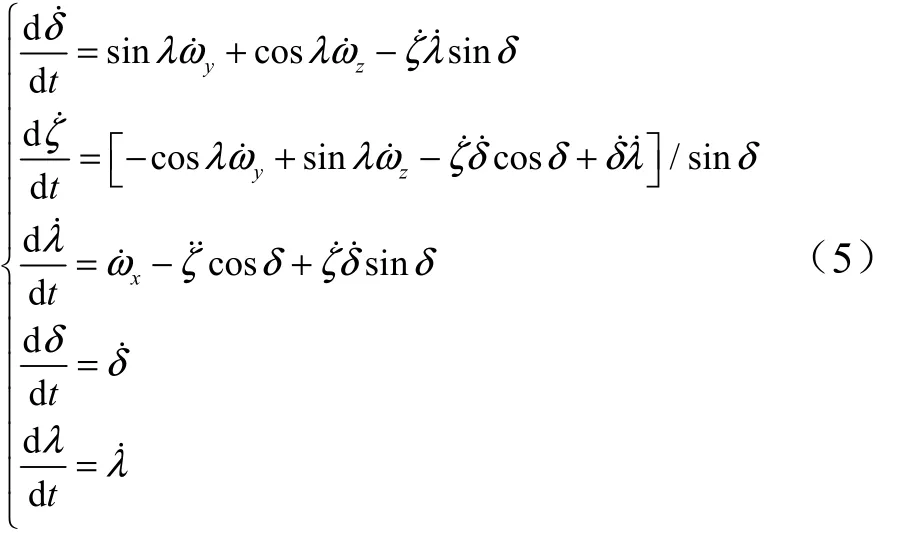
2 非線性模型平衡點求解

對于助推器再入飛行無控姿態動力學系統，為了得到系統在固定參數下的平衡點，需要將模型中的所有狀態變量關于時間的導數設為0。以上標“P”表示平衡點處的各狀態變量，則得到平衡點處的運動方程：

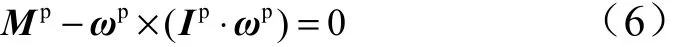
式中 Ip為彈體平衡點轉動慣量矢量； ωp為彈體平衡點角速度矢量； Mp為平衡點合外力矩矢量。

式（6）即為平衡狀態的運動方程，展開可得到平衡方程的標量形式為

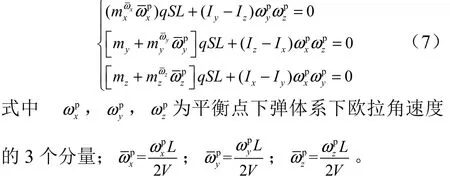
3 郭濤算法

針對高階強非線性方程組，在理論上不存在解析解，對于該問題的求解一般采用數值方法。比較常用的數值方法包括牛頓法和遺傳算法等，但這些算法對初值敏感，求解結果具有局部性，無法實現全局多解的求解，甚至在一些非線性較強的方程組求解過程中會出現直接發散的現象。所以有必要研究對于該類方程組的有效求解方法。

武漢大學的郭濤提出了一種演化搜索算法，其在求解非線性優化問題及多解問題時有獨特的優勢，能夠保證解的全局性，同時收斂速度較快，是一種適合解決本文問題的方法，其特點為：

a）提出了一種基于全局的群體搜索策略，理論上能夠保證解的全局性。

b）提出了種群迭代優化策略，采用遺傳算法中父代雜交與隨機子空間搜索并行策略，保證了在種群優化過程中兼顧搜索的遍歷性。

c）提出了末等淘汰策略，種群迭代中每次只淘汰最劣等個體，能夠較好地控制種群的整體性。

郭濤算法同時在理論上保證了全局性及遍歷性，這樣就保證了算法能夠依概率一收斂到全局最優解。

該方法的主要求解策略及流程如圖2所示。

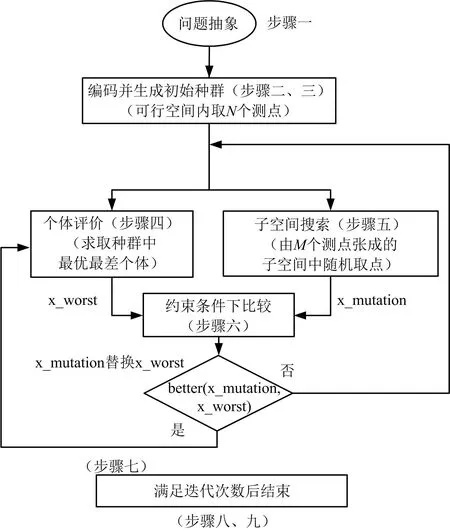
圖2 郭濤算法的求解過程Fig.2 Guo Tao Algorithm Solution Process

a）步驟一：問題的描述。

郭濤算法求解的第1步，將常見的非線性多維方程組多解問題抽象為有約束下的最優化問題。

設非線性方程組為

假定該方程組有解，其求解問題可以轉化為

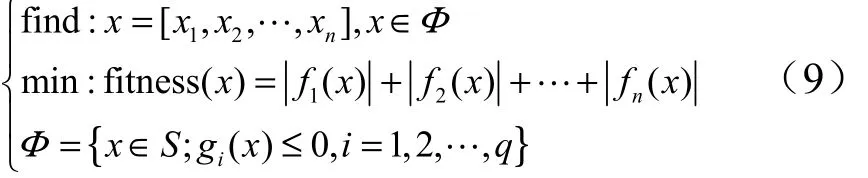
其中，S為搜索空間， S ?Rn，當fitness(x):S→R稱為目標函數，fitness(x)= 0 時，x為方程組的精確解，通常S是一個n維長方體，即由所確定；Φ為可行點集或可行區域。

b）步驟二：確定編碼方式。

確定問題的數學模型后，需要制定研究對象的編碼方式，對于復雜的非線性問題，采用浮點數編碼能夠提高算法求解的準確程度。

c）步驟三：種群初始化。

d）步驟四：個體評價。

本文的優化問題可歸納為連續優化問題，因為約束及解空間在實數空間上是處處連續的，因此針對該問題的求解過程能夠保證較好的局域性及精確程度。

用邏輯函數 b etter(x1, x2)表示測試點 x1優于測試點：

定義：

用定義的邏輯運算函數，求解種群中的最優個體xbest和 最 差 值xworst， 使 得 ： ?x∈P，better(xbest, x) ,better(x, xworst)；如果 b etter(xworst,xbest)，轉到步驟八。

e）步驟五：子代優化（父體雜交）。

以相同概率選取上述兩種方法中的一種決定搜索空間V，并在V中隨機選取一點x。

f）步驟六：劣汰策略。

如果better(x, xworst)，則xworst= x 。

g）步驟七：轉到步驟四。

h）步驟八：輸出 xbest。

i）步驟九：結束。

4 助推器再入三通道動力學特性分析

4.1 平衡點求解

求解平衡狀態非線性方程組時，氣動力系數通過攻角α和側滑角β在（-180°，+180°）范圍內插值得到，系統具有定義域范圍大和參數強非線性的特點（各特征馬赫數下法向力系數NC和俯仰力矩系數MZC的變化規律見圖 3、圖 4）。傳統解非線性方程組的方法如半解析法和牛頓法只能解決小定義域和參數定常的問題，不適用于本文的模型。郭濤算法采用變空間搜索及劣勢淘汰策略，對方程組解的搜索具有全局性，不受定義域大小的限制。同時由于郭濤算法基于演化搜索的思想，只要求模型參數可求，不要求其定常或可微，使得郭濤算法具有更強的適應性，適用于本文的參數強非線性模型。

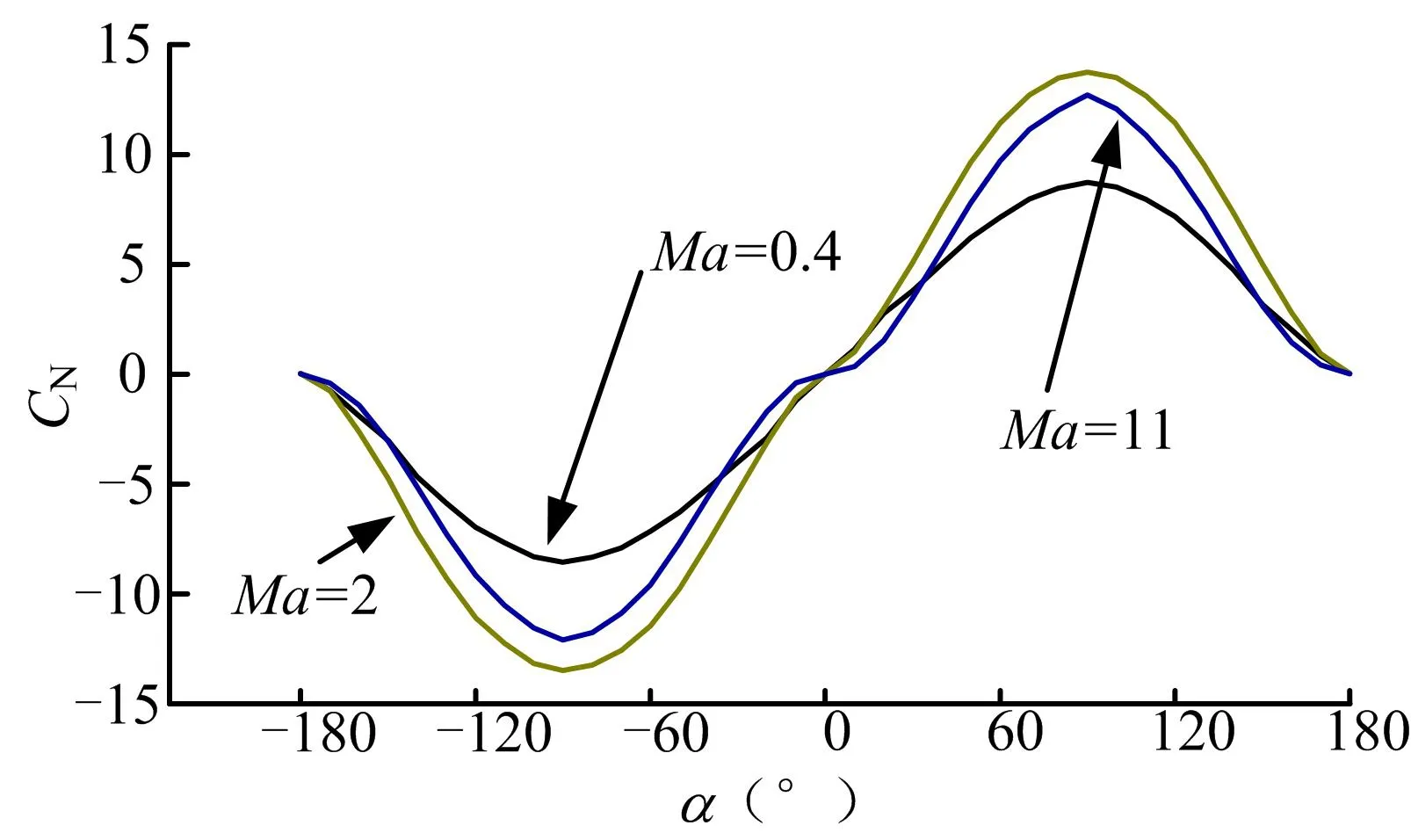
圖3 NC 隨攻角變化Fig.3 CN’s Relationship to the Change in Angle of Attack

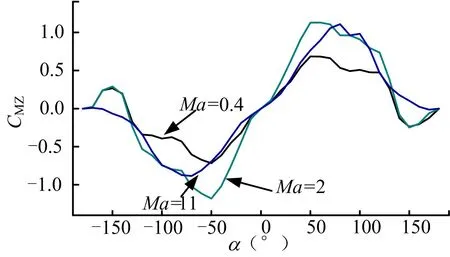
圖4 MZC 隨攻角變化Fig.4 CMZ’s Relationship to the Change in Angle of Attack

根據非線性微分方程組的特性和助推器氣動軸對稱的特點，可知若{ζ ˙ ,δ, λ}為方程組的一個解，那么{ζ ˙ ,? δ,π+λ}，{? ζ ˙, δ, ?λ}，{?ζ˙,? δ, π ?λ}也是方程組的解，且在這 4個解處，系統具有相似的姿態運動規律，可以認為它們代表1個解。因此在下文中僅給出一種解的形式作為相同動態特性解的代表，且如{0 ,π,0} 等顯而易見的解也不再記錄。最后通過郭濤算法仿真計算得到助推器在不同特征馬赫數下對應的非線性姿態運動的平衡點，見表1。

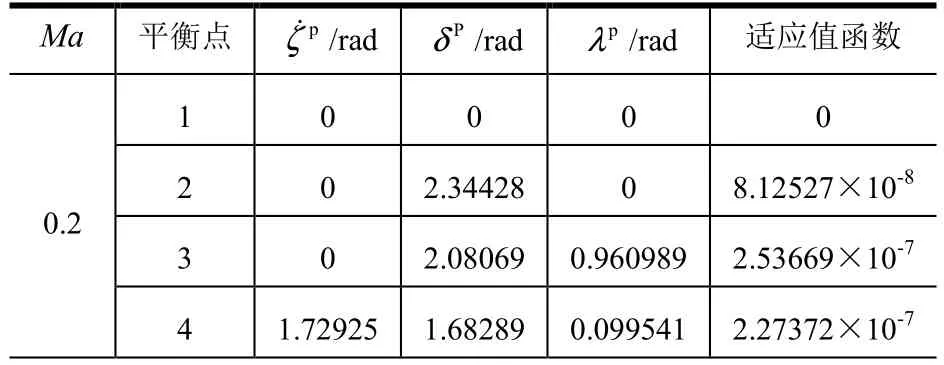
表1 郭濤算法解不同特征Ma下對應非線性模型平衡點Tab.1 Guo Tao Algorithm’s Solutions Depend on Diferrent Ma

續表1

由表1可知，利用郭濤算法求解出每個特征馬赫數下助推器姿態運動非線性方程組存在4組解，每組解對應的適應值函數均接近于零，表明算法精度較高，結果可信。

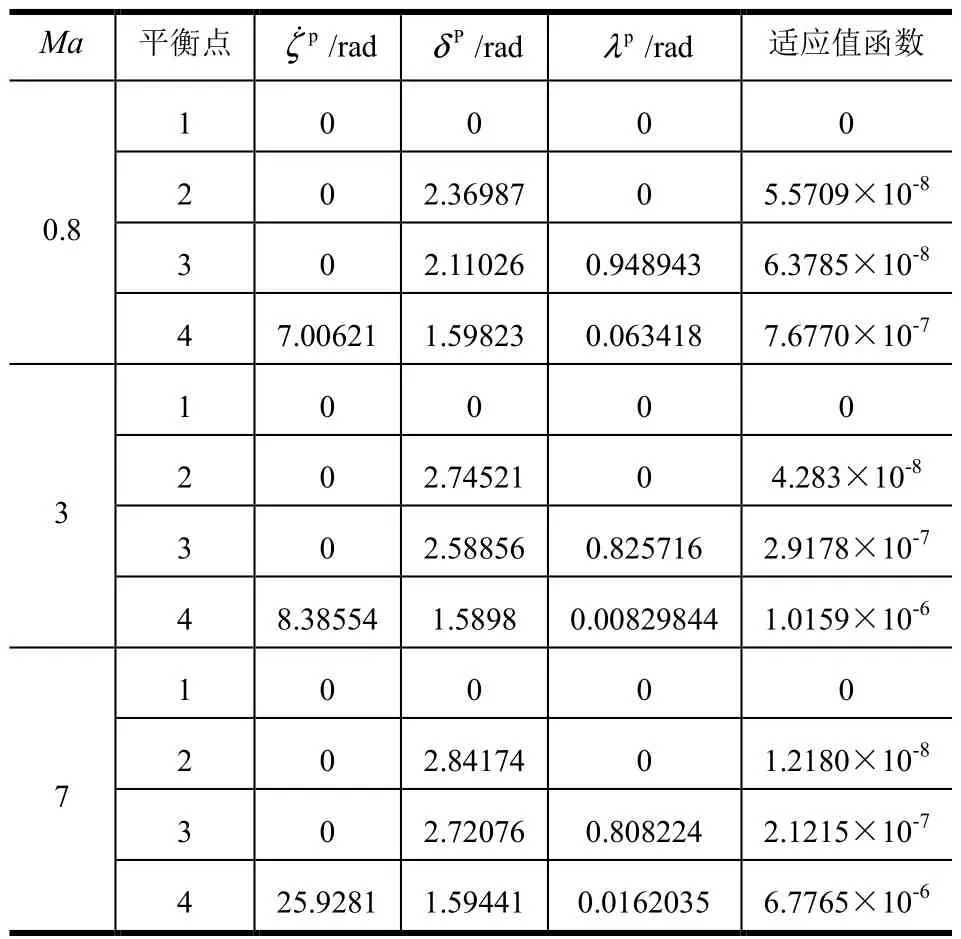
通過經典歐拉角的定義可知：ζ˙表征助推器的旋轉速度；δ表征助推器縱軸與速度軸夾角，等價于總攻角；λ表征助推器縱平面與總攻角平面夾角。通過表 1對不同特征馬赫數下的平衡點分析可以得到平衡點隨馬赫數變化的規律，見圖5、圖6。由圖5以及圖6的分析結果知，不同于線性系統，助推器非線性系統存在多組平衡點。不考慮對稱分布的相似平衡點，在再入馬赫數 M a∈ (1 ,9)的情況下分布著 4組平衡點：其中平衡點1對應δ=0°；平衡點2對應δ≈90°，隨著馬赫數的增加章動角變化不大，而相應的進動角速度隨馬赫數增加而增加；平衡點3、4對應δ隨馬赫數的增加而增加，由δ≈110°向δ≈160°變化。

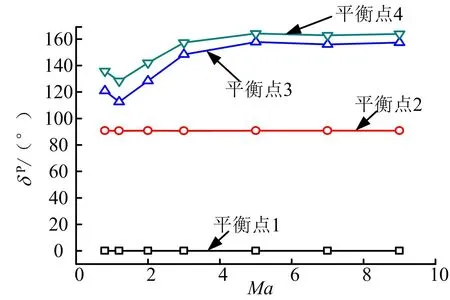
圖5 平衡點對應章動角隨馬赫數變化規律Fig.5 Pδ’s Relationship to the Change in Angle of Attack

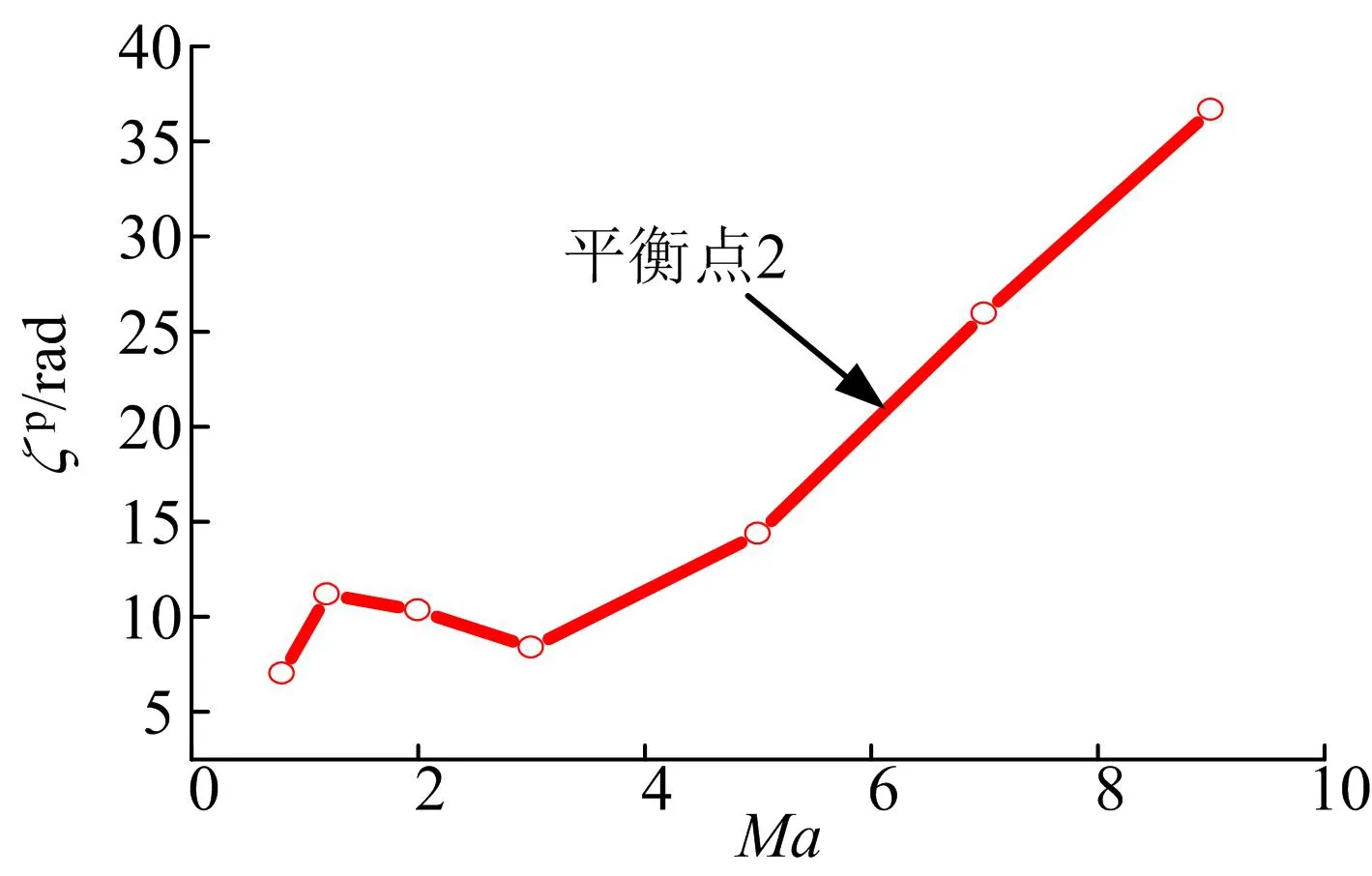
圖6 平衡點對應進動角速度隨馬赫數變化規律Fig.6 ζ ˙p ’s Relationship to the Change in Angle of Attack

4.2 平衡點穩定性分析

助推器再入姿態動力學是強耦合高維非線性系統，很難直接根據李雅普諾夫穩定性的定義來判斷其穩定性。對于此類非線性系統，李雅普諾夫第一法（或稱間接法）在穩定性的分析中具有著廣泛的應用。

李雅普諾夫第一法（間接法）：

若x=0是非線性系統 x˙ =f( x)的一個平衡點，其中f →Rn是連續可微的，設雅克比矩陣為

如果D的所有特征值都滿足 R eλi< 0，則原點是漸近穩定的；

如果D至少有一個特征值滿足 R eλi> 0，則原點是不穩定的；

如果有某一解的特征根實部在零點而其余特征根的實部為負值，此時則無法判斷該平衡點的穩定性。

運用Lyapunov的第1種方法求解本文再入非線性系統平衡點的穩定性，可分析得到平衡點的穩定性隨馬赫數變化規律，可得到再入助推器姿態動力學平衡點穩定性的變化規律，見圖7。

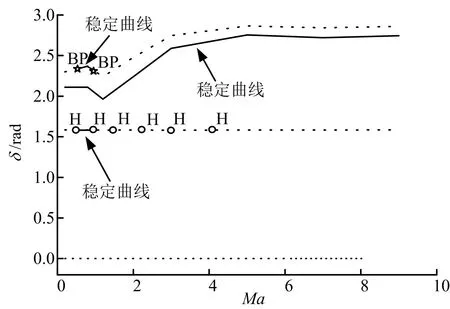
圖7 δ解曲線的穩定性Fig.7 Stability of the δ’s Solution

由圖7可知，在助推器再入飛行絕大部分馬赫數域內，非線性系統具有一組穩定平衡點和3組不穩定平衡點，這意味著在合適的初始條件下系統會被鎖定在這一平衡狀態下。而在Ma∈（0.76,0.84）這一馬赫數域內，系統的2組不穩定解曲線發生了性態變化，演變成穩定平衡解曲線，此時系統存在3組穩定平衡點，意味著在合適的初始條件下系統可能被鎖定在其中任意一種平衡狀態下。此處以Ma=0.8的工況為例，將不同初始狀態對應的相軌跡在δ-δ˙平面上進行投影，所得結果如圖8所示。

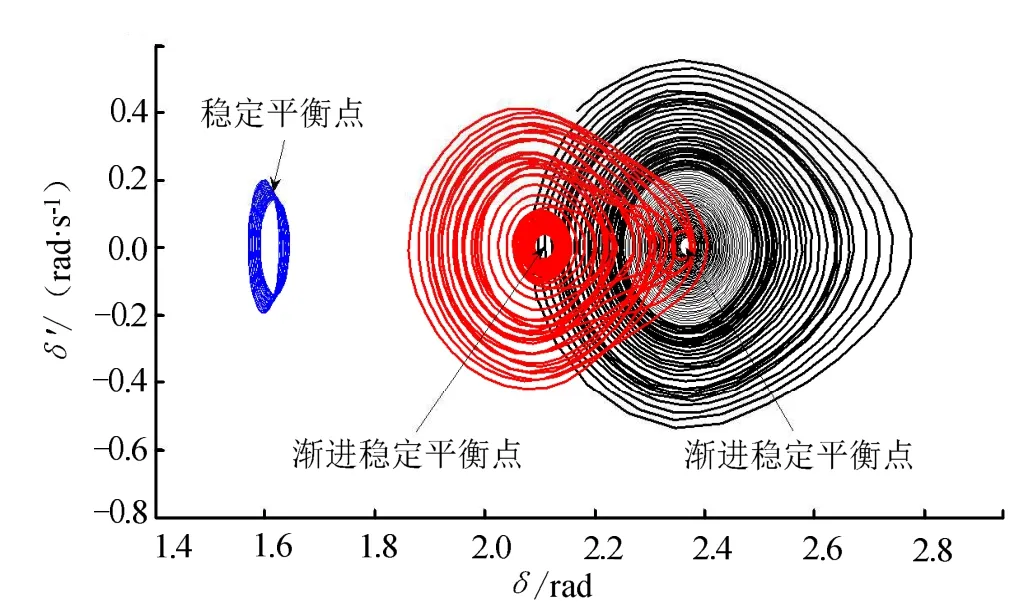
a）相軌跡在δ-δ˙平面上進行投影

續圖8

圖8 中不同曲線代表的是不同初始條件對應的相圖在δ-δ˙平面的投影，從圖 8中可以看到在仿真工況下的吸引子包括2個漸進穩定的平衡點和一個穩定的極限環，不同的初始條件會使得助推器的姿態收斂到不同的吸引子，驗證了基于演化搜索算法求解的平衡狀態的正確性。

將不同初始狀態對應的相軌跡在t-ζ˙平面上進行投影，所得結果如圖9所示。

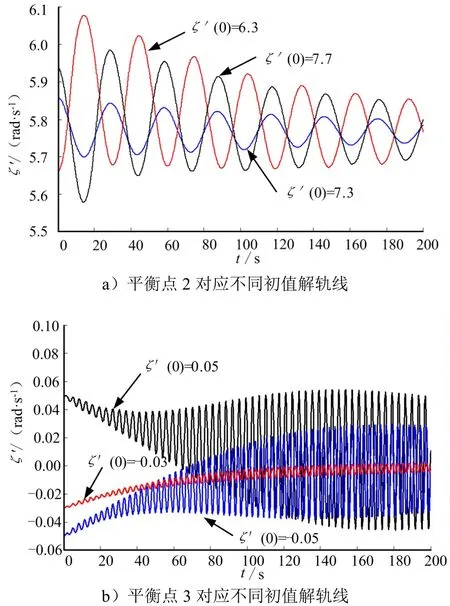
圖9 解軌線在t-ζ˙平面投影Fig.9 Solve for the Projection onto t-ζ˙ Plane

由圖9可知，在Ma=0.8的工況下，在進動角速度存在初始偏差的情況下，均能收斂到平衡點對應的穩定狀態（平衡點2和4）或在平衡點對應穩定狀態附近震蕩（平衡點3），其中平衡點2對應的穩定進動角速度ζ˙為7.006 21，平衡點3和4對應ζ˙為0。再次驗證了平衡點解算的正確性。

5 結 論

本文采用基于演化搜索策略的郭濤算法，解決了助推器再入飛行模態的預示問題。首先推導了以經典歐拉角描述的姿態運動模型，使研究結論更直觀，模型更簡潔。利用該模型，進一步推導了五維姿態動力學平衡點方程組，并采用基于演化搜索算法的改進郭濤算法解決了非線性方程組的多解問題。進一步，利用Lyapunov第一法對平衡點穩定性進行了分析。最后通過了時域分析的驗證。結果表明在再入過程中的特定馬赫數域內（Ma=（0.76，0.84））存在3組飛行模態，一組模態對應高速旋轉運動，其余兩組模態對應姿態穩定運動。進入該飛行速域時的不同初始狀態將使助推器姿態運動收斂到不同的飛行模態。

本文提出了助推器無控飛行模態的預示方法，獲得了再入飛行速域內助推器可能出現的多個穩定飛行模態，為進一步設計助推器回收系統或精細化設計安控區提供了有力支撐。但本文并未對各模態的穩定域進行分析，如何解決高維非線性模型穩定域的確定將是下一步研究的重點。