基于落速預測理論的子母彈拋撒高度優化算法

劉 賽，李長春，朱 敏，李宇鵬，熊學文

（北京航天長征飛行器研究所，北京，100076）

0 引 言

導彈是現代戰爭中的主要兵器之一，子母戰斗部由于其能夠有效擴大針對目標的覆蓋面積，在導彈武器發展中得到了廣泛的應用，如果按照目標特性和毀傷效果對子母彈系統進行優化設計，則能夠大幅提高子母戰斗部的毀傷效能。

子母戰斗部最終的毀傷效能由子彈數量、威力及其落點分布決定。子彈的落點分布主要取決于母彈的彈道參數特性、子彈的氣動特性、子母彈拋撒特性和子彈的拋撒高度等因素。文獻[1]和文獻[2]均對子母彈的拋撒半徑優化技術進行了研究，其研究成果均可作為子母彈拋撒半徑的優化設計方法；文獻[3]和文獻[4]對子母彈開艙高度的高低散布因素進行了分析，提出了敏感參數和敏感度的概念。可見對于子母彈，拋撒半徑是一個非常重要的戰術技術指標，針對拋撒半徑開展優化分析工作也是研究的熱點。

本文首先對子彈飛行彈道進行建模，然后根據落速預測的理論對母彈飛行至理論拋撒高度時的速度進行預測，并設計了一種重新計算拋撒高度的算法，根據該算法的計算結果在空中重新裝訂拋撒高度，通過仿真計算結果統計，應用該方法后的子母彈拋撒半徑誤差將明顯減小。

1 動力學建模

導彈拋撒子彈時已經進入導彈的飛行末段，通常此時的飛行高度較低，在研究子母彈拋撒技術時，可以把地球看作其圓球模型與拋撒時母彈海平面高度彈下點相切的平面大地，在大地平面中建立拋撒點當地坐標系，如圖1所示。

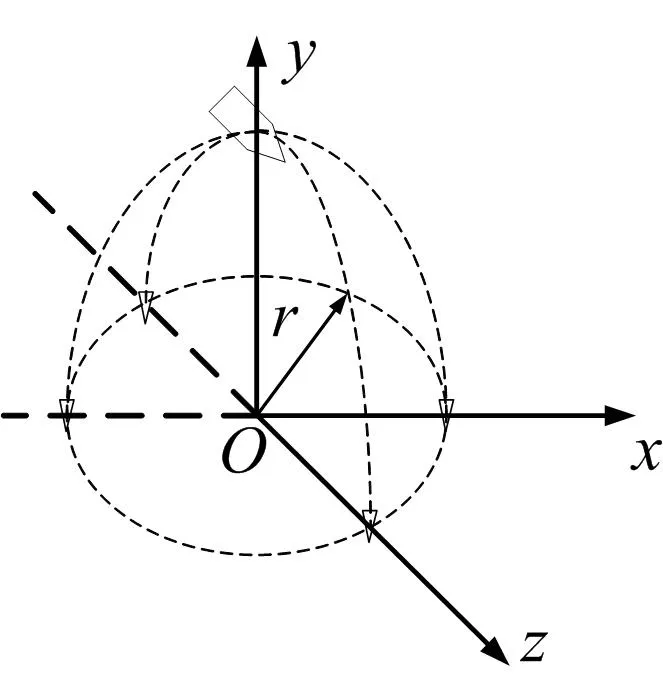
圖1 子彈拋撒坐標系、拋撒半徑定義Fig.1 Definition of Dispersion Coordinate System and Dispersion Radiusr—拋撒半徑

原點O為上述的切點，Oy軸垂直于大地平面指向母彈的拋撒點，Ox軸在平面內指向母彈速度矢量在平面投影的方向（若速度方向垂直于平面，則可以任意選擇x軸方向），Oz軸按右手定則確定。

把母彈和子彈視為穩定的質點，在拋撒點當地坐標系中建立子彈的飛行動力學和運動學方程：

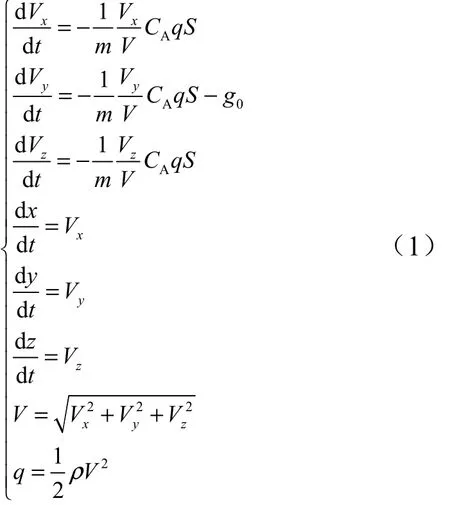
式中 x，y，z為子彈在拋撒點當地坐標系中的坐標；Vx， Vy， Vz為子彈速度矢量在拋撒點當地坐標系中各軸上的投影；V為子彈相對拋撒點當地坐標系的速度；m為子彈的質量； CA為子彈軸向力氣動系數即阻力系數；q為動壓；ρ為大氣密度； g0為重力加速度，考慮導彈拋撒高度高度通常在5 km以下，重力加速度變化較小，為簡化公式推導，取為海平面重力加速度，9.806 65 m/s2。

對式（1）進行數值積分，可以計算出子彈的落點。在計算子彈落點的拋撒半徑時，可以簡化計算前、后、左、右4枚子彈的落點，然后根據落點坐標計算等效圓半徑。在計算不同落點子彈的積分初始條件中，子彈的位置坐標相同即母彈的位置：

式中0h為母彈在拋撒點的高度。

各子彈的初始速度不同，前落點子彈初始速度為

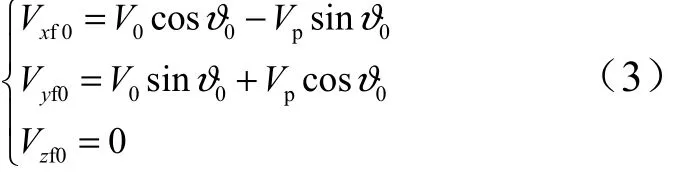
式中0V為母彈在拋撒點相對拋撒點當地坐標系的速度；0?為母彈在拋撒點的當地彈道傾角；pV為拋撒子彈的最大速度。

后落點子彈初始速度：

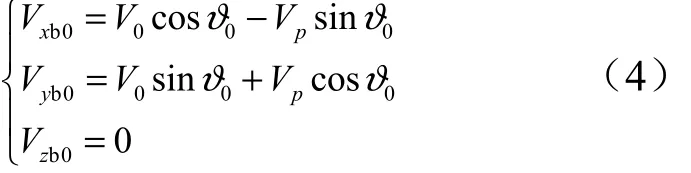
左落點子彈初始速度：

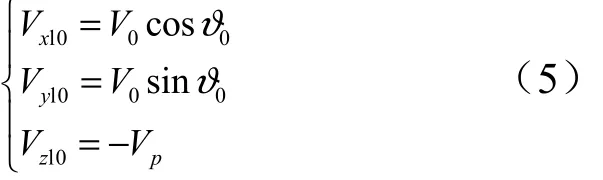
右落點子彈初始速度：

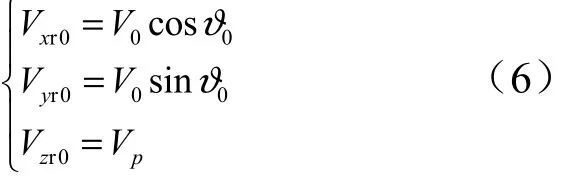
以式（2）～（6）為初始條件，對式（1）進行數值積分，計算得到子彈的前、后、左、右落點，坐標分別為：，其中 hc為落點高程，m。

計算拋撒半徑r：

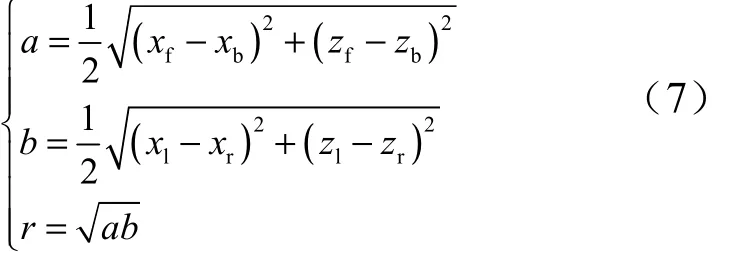
2 落速預測理論

通常情況下，很難得到母彈飛行動力學的解析解，但是當母彈在距離目標較近的情況下，通過以下一系列假設，有利于得到落速解析解：

a）因母彈離目標較近，可以只考慮俯仰平面飛行器的動力學方程；

b）母彈的當地彈道傾角變化范圍較小；

c）母彈落速的馬赫數在較小的變化區間中，且不涵蓋亞跨聲速范圍，母彈阻力系數 Cx取常值（可以根據經驗進行適當修正）；

d）母彈拋撒前攻角近似為0；

根據以上假設，得到再入飛行器運動的動力學方程[7]：

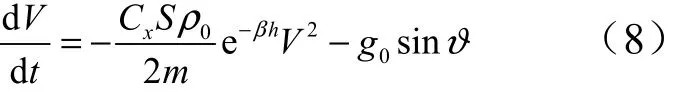
對式（8）進行變量替換，可得：

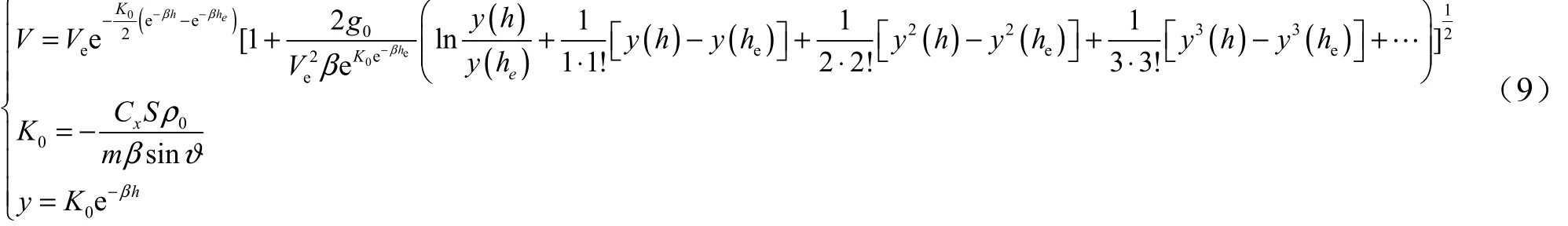
式中eV為進行預測時母彈的速度；eh為進行預測時母彈的高度。

使用式（9）計算時，可以根據需要保留不同階數，在本文的計算中，保留二階。

3 拋撒高度優化算法

綜合式（1）～（7）可得：

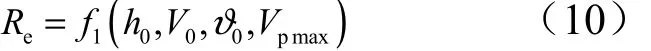
根據式（10）的全微分可以近似得到[8]：

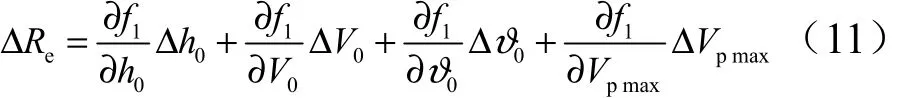
式中 Re為拋撒半徑；?Re為拋撒半徑偏差。

在導彈方案已經確定的情況下，在飛行末段拋撒參數?0和Vp很難通過主動控制改變，因此可以認為在式（11）中，??0=0，?Vpmax= 0 ，式（11）簡化為如下形式：

如果導彈仍在原理論高度進行拋撒，即00h?=，可以得到：

根據式（9），即可求出導彈在原理論高度的速度與理論速度的偏差0V?，從而根據式（13）求出導彈在原理論高度拋撒時的拋撒半徑偏差eR?。本文設計一種空中裝訂拋撒高度的算法，計算導彈需要調整的拋撒高度，將該高度裝訂至導彈的引爆控制系統中，導彈將根據新裝訂的高度進行拋撒，以抵消式（13）的偏差，從而減小拋撒半徑的誤差帶。

根據式（12）可以近似得到：

其中，可以根據式（9），以0V和0h替換式（9）中的V

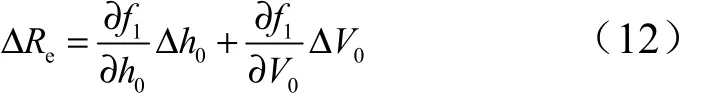
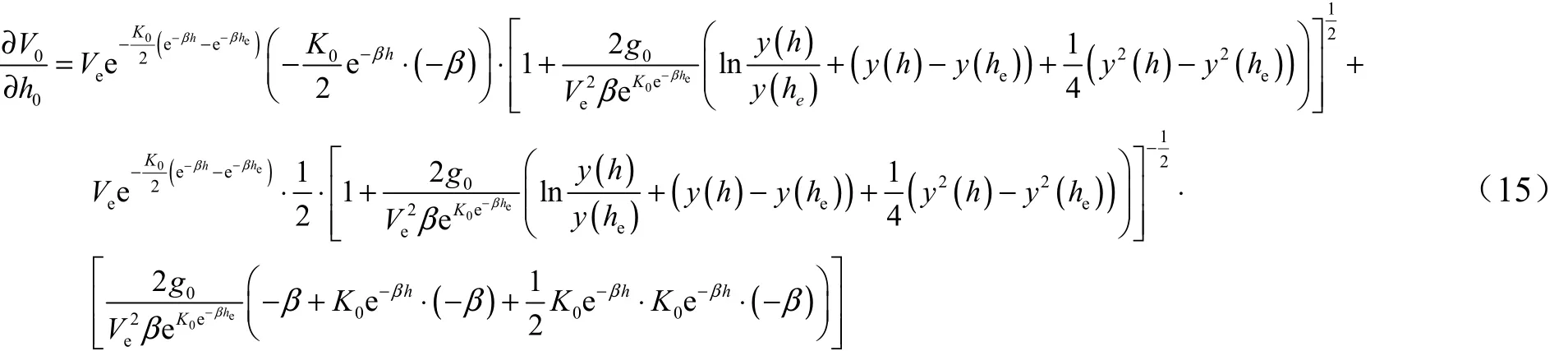
根據式（13）、式（14），為抵消由拋撒點速度偏差0V?帶來的拋撒半徑偏差，可以得到：

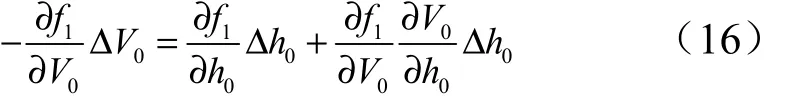
整理式（16），得到：

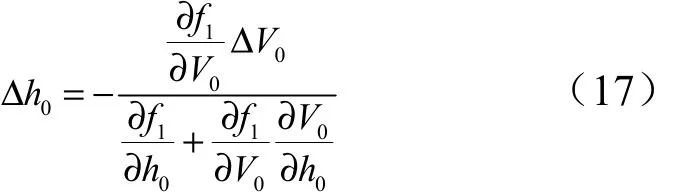
式中 ?h0為在原拋撒高度基礎上需要調整的高度；? V0為根據式（9）預測的速度與導彈理論速度的差（均在原理論拋撒高度上）。

將式（15）的計算結果代入式（17），即可得到導彈需要調整的拋撒高度。

4 仿真計算

根據上文的算法計算1個算例：

假設導彈最大拋撒速度為40 m/s，設計拋撒高度為2000 m，拋撒時母彈速度為1000 m/s，拋撒時母彈當地彈道傾角為-60°，當母彈飛行至5000 m時進行落速預測并裝訂優化后的拋撒高度。

初始條件代入式（1）～（6），計算得到拋撒半徑為96.9 m。拋撒半徑對拋散參數的偏導數如表1所示。

表1 偏導數計算結果Tab.1 Computational Results of Partial Derivatives

考慮母彈質量、母彈速度、母彈當地彈道傾角、母彈氣動力系數、子彈質量、子彈氣動力系數和大氣密度等偏差，應用Monte Carlo法打靶計算1000條彈道，統計按理論高度拋撒的拋撒半徑結果和按算法裝訂拋撒高度的拋撒半徑結果。

母彈和子彈拋撒參數和特性參數的誤差如表2所示。

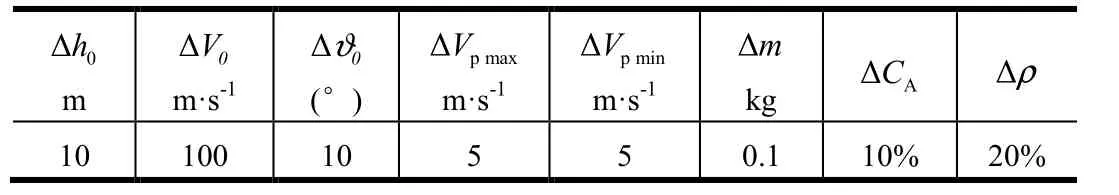
表2 拋撒參數和特性參數的誤差Tab.2 Errors of Dispersion Parameters and Characteristic Parameters

統計結果如表3所示。

表3 拋撒半徑統計結果Tab.3 Statistical Result of Dispersion Radius

5 結 論

本文設計的優化算法簡單，利于導彈在空中進行拋撒高度的計算裝訂，應用本算法后，可明顯地減小子母彈拋撒半徑的誤差帶，有益于精確控制子母彈的拋撒半徑，從而實現最優的毀傷效果。

同時，子彈出艙后的拋撒姿態、子彈氣動穩定性、母彈激波層等會為子彈帶來飛行穩定性的影響，從而會影響子彈散布，對此本文未進行分析，這也將是后續研究的方向。但是，可以根據地面試驗和飛行試驗獲取的數據對本文所述的方法進行修正，主要是修正母彈和子彈的阻力系數，修正后的方法仍可以適用于工程應用。