應用速燃發動機技術的固體運載器優化設計

黃體圣，趙 民，姜 利，孫勇強，王鵬飛

（1. 北京宇航系統工程研究所，北京，100076；2. 中國運載火箭技術研究院，北京，100076）

0 引 言

作為一種重要的航天運載器，多級固體運載器具有響應速度快、機動性強、成本低、可靠性高的特點，目前已成為各國研究的熱點[1]。國內外眾多研究者對固體運載器的總體參數優化設計方法進行了研究，在研究中一般選取運載能力最優為目標函數[2～4]。但作為復雜的系統工程，在追求運載能力最優的同時，也應兼顧其它性能指標，如效費比、可靠性、生存能力等，而面對日益復雜的應用環境，生存能力的重要性也愈來愈突出。

在固體運載器飛行過程中，一般可分為主動段和被動段（包括飛行中段和再入段），其中主動段發動機紅外特征明顯，是生存能力較為薄弱的階段[5]。速燃發動機可顯著降低固體運載器主動段高度，被認為是提高主動段生存能力的有效手段[6]。

采用速燃發動機后，一方面固體運載器飛行條件惡化，氣動阻力損失大大增加；另一方面發動機流量增大、噴管喉徑增加，必然帶來發動機質量比的下降，與運載能力最優的目標相矛盾。因此在應用速燃發動機技術的固體運載器方案論證階段，需對運載能力及生存能力進行綜合權衡。多目標優化是解決這類問題的有效手段，可得到所有的非劣解構建非劣解集，而后根據經驗從中選取合適的解。

本文針對三級固體運載器，選擇主動段高度最小和射程最大為目標函數，應用NSGA-Ⅱ算法完成固體運載器的多目標優化設計研究。

1 系統設計模型

在固體運載器的設計過程中，一般涉及發動機、彈道、氣動、姿態控制及載荷計算等多個學科[7,8]。其中發動機是固體運載器最主要的部件之一，決定了固體運載器的構型及性能水平，而彈道設計確定了固體運載器的飛行彈道，是評價其總體性能好壞的核心依據，因此本文選擇這兩個關鍵學科構建固體運載器系統設計模型。

1.1 發動機設計模型

由于發動機設計對固體運載器的構型及性能水平具有決定性作用，可選擇發動機的設計變量作為固體運載器系統設計模型的輸入變量。固體發動機設計變量的選取有多種方式，一般選取一組相互獨立的設計變量[9]，本文選擇的設計變量為：發動機直徑mD、裝藥量pm、工作壓強cP、發動機工作時間wt、噴管擴張比ε，其中發動機直徑mD根據已有型譜確定，不參與優化。

固體發動機主要由裝藥、燃燒室殼體、噴管及點火裝置等組成，為提高固體運載器性能，本文選用硝酸酯增塑聚醚（Nitrate Ester Plasticized Polyether ，NEPE）推進劑裝藥、復合材料殼體及噴管。

固體發動機的設計流程較為成熟，主要需對發動機的能量特性、質量及尺寸進行計算。能量特性的關鍵是對發動機比沖進行預估，其計算公式為

式中 C*為特征速度，可視為常量，由熱力計算提供；CF為推力系數；ηcf為比沖效率，可采用回歸方程形式的經驗公式進行計算[2]，即：

式中td為噴管喉部直徑，cm；β為噴管擴張半角，（°）；AlW為推進劑中鋁粉含量的百分比；ε為噴管擴張比。

推力系數FC可由下式計算：

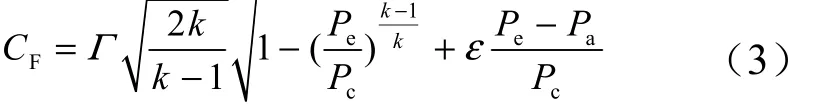
式中 Γ為比熱比函數；k為比熱比；aP為環境壓強；為噴管出口壓強。

對于發動機質量計算，為保證計算精度，采用展開型質量模型分別計算燃燒室殼體、絕熱層、噴管、前后接頭等部件結構質量，質量模型的具體建立過程參見文獻[2]。同時，對燃燒室殼體及發動機噴管的尺寸參數進行計算，以獲得發動機的整體尺寸。

由設計變量通過發動機設計模型計算可獲得各級發動機的性能、質量及尺寸參數。對于方案論證階段，可認為運載器級間段、電纜網、控制儀器等部件的質量與各級發動機質量成正比，取適當的無因次系數即可獲得運載器的各級起飛質量，供彈道設計模型使用。

1.2 彈道設計模型

1.2.1 飛行程序角設計

采用常用的工程設計方法對固體運載器主動段的飛行程序角cx?進行設計[10]，飛行程序角曲線如圖1所示。

圖1 主動段飛行程序角曲線Fig.1 Power Flight Programming Angle Curve

具體飛行時序為：點火起飛后，零攻角垂直飛行至t1時刻，t1由運載器推重比確定；此后利用攻角轉彎調整推力方向至t2時刻，攻角轉彎的最大負攻角為αM，是彈道設計模型的設計變量， t2選擇運載器的馬赫數為0.7～0.8；而后保持零攻角穿越稠密大氣，以減少氣動載荷，同時利用重力進行轉彎，t3選擇為大氣稀薄時的高度；最后是定軸飛行段，保持俯仰角不變直至主動段結束。

采用該種程序角設計方法，彈道設計模型只有αM一個變量，由于再入點的當地彈道傾角是影響飛行彈道形態的關鍵約束，因此，可通過求解方程Θr= Θrmax的方式確定αM，避免了αM參與系統層的優化，提高了系統層的優化效率。

1.2.2 彈道計算模型

考慮地球為標準圓球體，不考慮地球自轉，采用標準大氣模型，在發射系內建立運載器的三自由度質心運動方程[11]，即：

式中 下標x，y，z分別為位置向量在發射系下的分量；Vx， Vy， Vz為速度向量在發射系下的分量； GB為彈體坐標系至發射坐標系的轉換矩陣；m為運載器質量；P為發動機推力； GV為速度坐標系至發射坐標系的轉換矩陣；X，Y，Z分別為運載器的氣動阻力、升力和側力，本文選擇泰坦2火箭的氣動力系數進行計算；gx，gy，gz分別為引力加速度在發射系下的分量； m0為運載器起飛質量；m˙為發動機燃氣秒流量。

2 優化模型建模

2.1 優化目標

綜合考慮固體運載器的運載能力和主動段的生存能力，目標函數選擇為：最大化射程L、最小化主動段高度PH。

2.2 約束條件

為限制固體運載器規模，應對固體運載器的起飛質量0m和長度0L進行限制；為限制固體運載器主動段氣動載荷及加熱量，應對飛行最大動壓mq進行限制；考慮到一、二級分離的安全性，應對分離高度sH進行限制；為保證有效載荷中的電子元件正常工作，需對運載器飛行過程中的最大軸向過載xN進行限制。

綜合設計變量、優化目標及約束條件，固體運載器系統的優化模型數學表述為

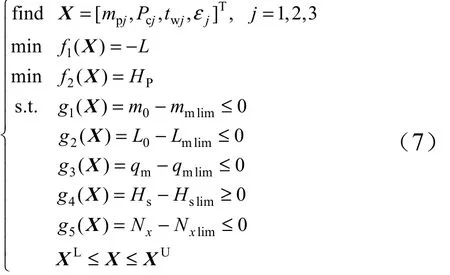
式中 下標：j為發動機級數，lim為各約束的限定值；X為設計變量； XL， XU分別為設計變量的取值下限和上限。

2.3 優化算法

對于求解多目標優化問題，主要有歸一化算法和非歸一化算法兩大類[12]。歸一化算法是采用加權法、約束法和目標規劃法等手段將多個目標轉化為單一目標，但為了獲得Pareto最優解集，必須運行多次優化過程，求解效率低。非歸一化算法是采用Pareto機制直接處理多個目標的優化技術，不需要將多個目標轉換為單一目標，并且能夠使所求解集盡量均勻覆蓋Pareto前沿，避免了歸一化算法的缺陷，在多目標優化問題中得到廣泛的應用。

在移動互聯網時代高速發展的今天，中國鐵路沈陽局集團有限公司如何利用互聯網+的思維模式實現管理轉型與創新，特別是對集團公司內部的審批業務模式的改革與升級勢在必行。

非支配排序遺傳算法（NSGA-Ⅱ）是最具代表性的非歸一化算法，該算法是在傳統遺傳算法的基礎上發展而來的，其基本思想是首先對父代種群進行遺傳操作，得到子種群，再將父代和子代種群合并，而后進行非支配排序和擁擠距離排序，得到新的種群，反復進行直到算法設置的最大迭代次數[13,14]。NSGA-Ⅱ算法具有優秀的探索能力，在多目標優化問題中得到廣泛應用，本文也采用該算法進行求解。算法參數設置為：種群規模100，進化代數100，交叉概率0.9，交叉分配指數20，變異分配指數100。

本文構建的優化模型如圖2所示，實現方法為采用 C++語言編制發動機及彈道設計模型，通過優化軟件Isight進行集成優化。

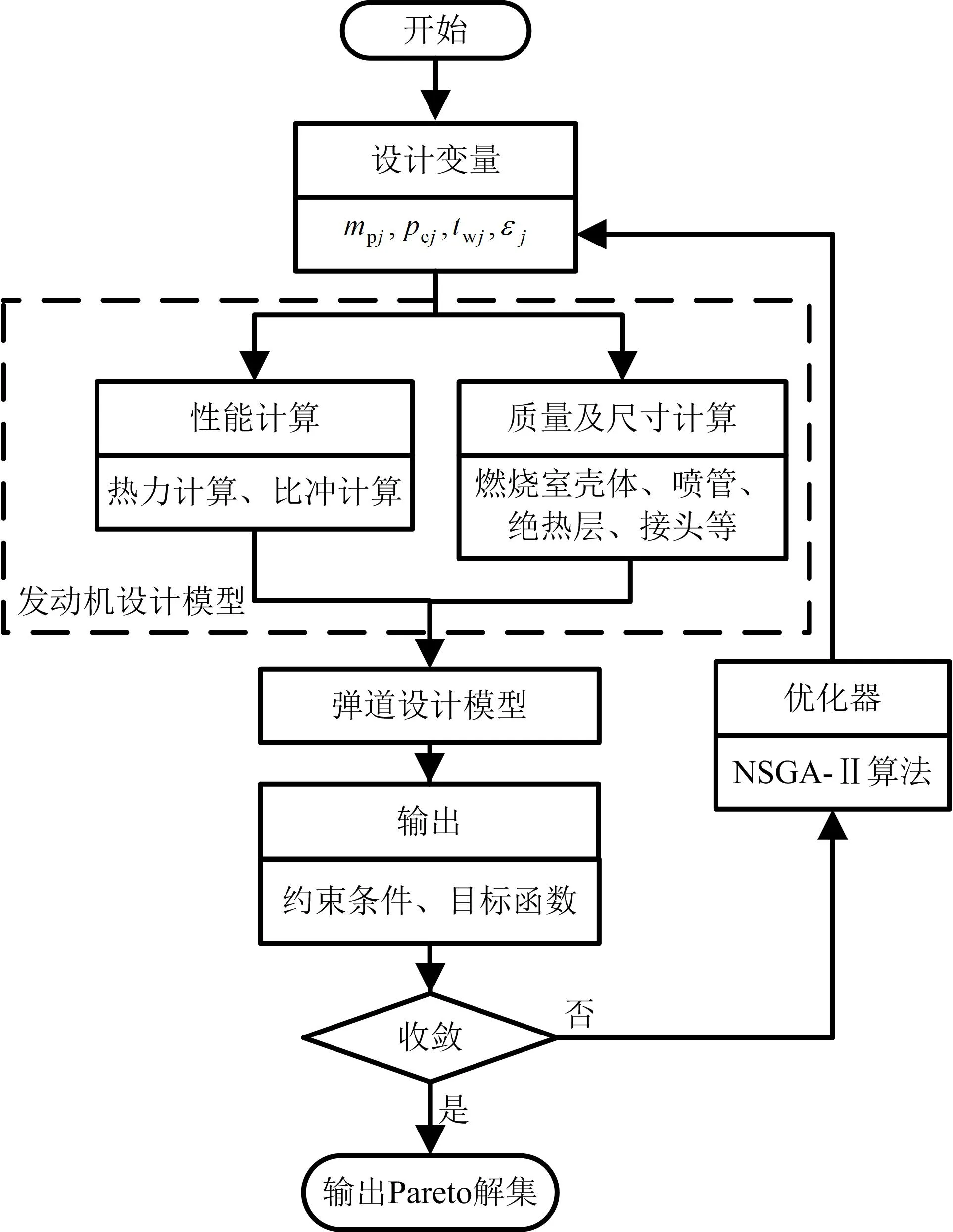
圖2 固體運載器多目標優化模型示意Fig.2 Multi-objective Optimization Model of Solid Launch Vehicle

3 仿真分析

3.1 仿真條件

某固體運載器的總體任務需求及約束條件為：有效載荷1.5 t，起飛質量0m不大于50 t，長度0L不大于18 m，飛行最大動壓mq不大于150 kPa，分離高度sH不低于20 km，最大軸向過載xN不大于40g。在實例優化仿真中，設計變量的優化區間如表1所示。

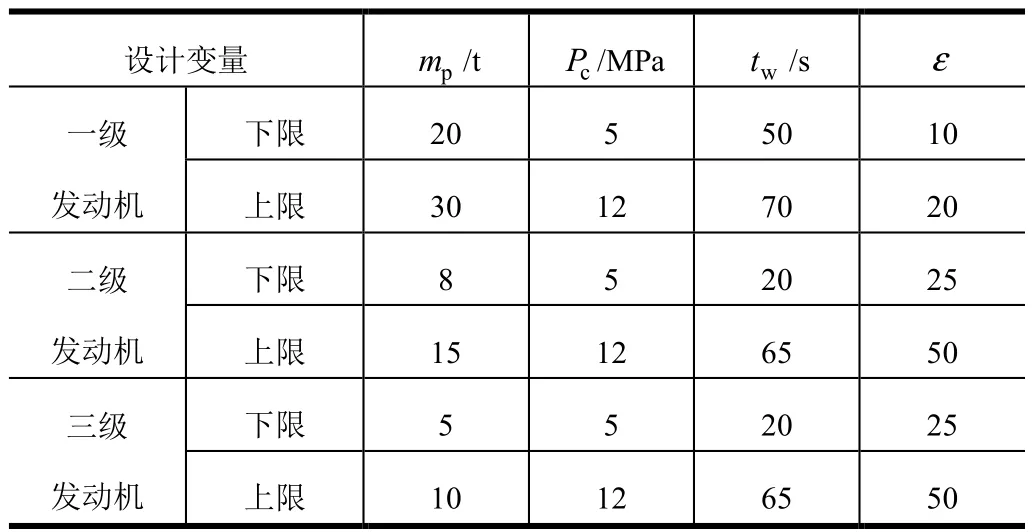
表1 設計變量的優化區間Tab.1 Optimal Interval of Design Variables

3.2 優化結果及分析

采用本文所構建的固體運載器系統優化模型進行仿真分析，獲得的Pareto前沿如圖3所示。

圖3 Pareto前沿Fig.3 Pareto Frontier

由圖3可知，采用NSGA-Ⅱ算法優化得到的Pareto前沿分布較為均勻，且散布范圍廣，可滿足固體運載器系統優化設計的要求。此外，圖3表明主動段高度越低，射程損失增加的越快，當主動段高度低于80 km時，射程損失急劇增加，因此在方案綜合決策時，主動段高度不宜過低。

表2和表3給出了Pareto解集中的具有代表性的解及其相應的性能參數，表3中1r，2r和3r表示各級發動機燃速。圖4和圖5給出了這3個解的主要彈道特征曲線。

由表2和表3可知：

a）相比于正常燃速的方案3，方案1的射程損失約1800 km，但主動段結束高度為75 km，是方案3的一半，這對運載器主動段生存能力的提高大有好處；

c）為降低主動段高度，一級發動機燃速變化不大，主要需增大二、三級發動機燃速，方案1的燃速需增加至方案3中正常燃速的2.5倍左右，可通過添加燃速調節劑實現，美國在實際工程中應用的NEPE推進劑燃速可達30 mm/s[6]，達到表中各方案所需燃速，可以實現75～100 km大氣層內關機是可行的。

表2 固體運載器部分設計結果Tab.2 Partial Design Results of SLV

表3 固體運載器部分設計結果的性能參數Tab.3 Performance Parameters for Partial Design Results of SLV

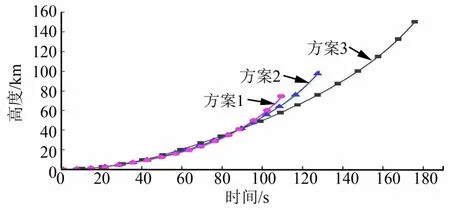
圖4 主動段高度隨時間變化曲線Fig.4 Curve of Height for Power Flight

4 結 論

采用NSGA-Ⅱ算法開展多目標優化分析，得到如下結論：

a）針對固體運載器多目標優化問題，可采用NSGA-Ⅱ算法僅通過一次優化仿真獲得分布均勻、散布范圍廣的Pareto解集，方便進行綜合決策；

b）對于不同主動段高度的設計方案，二、三級發動機設計參數變化較大，主要體現在隨著主動段高度的下降，工作時間縮短及燃燒室壓力升高；

c）當固體運載器主動段高度低于80 km時，運載能力損失急劇增加，在方案綜合決策時，不宜選擇過低的主動段高度。