基于問題的學習讓中職學生數學思維活起來

劉秋女

一、背景分析

數學思維，通常所指的是數學思維能力，即能夠用數學的觀點思考問題和解決問題的能力。基于問題的學習是以問題貫徹學習內容，將學習內容與學生的學習經驗聯系起來，把問題解決作為手段和目標。它與當前中小學提倡的自主探究、合作學習等多種學習方式相似，能有效地促進學生數學思維品質的發展，有助于更好地將枯燥乏味的數學理論課程轉化為學生體驗課程。自2010年起，廣州市中等職業學校每兩年開展一次數學應用（思維）能力競賽，迄今為止共舉辦6次，目的在于提高學生的數學思維及數學應用能力。那如何將日常教學與比賽備賽結合起來，讓更多的學生數學思維與應用能力能在常態化數學教學中得以發展，筆者以人教版“函數單調性”一課為例，根據學生數學學習的實際基礎，科學設計問題并以問題學習為切入口，探索如何在中職課堂中激起學生思維碰撞的火花，讓中職學生數學思維活起來，最終形成愿意思考、會思考的數學課堂。

二、教學案例

【教學內容】

《數學（基礎模塊）上冊》（人民教育出版社）P66-P68，《3.1.3 函數的單調性》。

【教材分析】

函數的單調性從函數圖像的角度出發，學生并不難理解，但要把這種直觀認識上升為理性認識，即用符號語言刻畫和描述函數的單調性時，大部分學生就有一定的困難，這個時候需要教師的引導與點撥，因此本節課重在函數單調性定義的形成及理解上，這也就是這節課所要重點解決的問題。且這種由圖像到數學符號的數學學習思維也貫通了函數另一個性質——《函數奇偶性》的學習。

【教學目標】

1.函數單調性定義的理解及簡單應用;

2.基于問題的學習中，體驗函數單調性定義的“生成過程”，搭建數學思維階梯，提升數學思維能力。

【教學重難點】

函數單調性定義的形成與理解。

【教學過程】

（一）課前微課學習

1.觀看微課視頻《函數的單調性》（圖1）以及完成相關在線試題（圖2）。

評析：通過課前微課告知學生的學習內容，學生在“微課”學習中遺留下的一些不理解的知識為課堂學習提供了一個重要的解決問題的契機。

（二）開門見山，提出問題

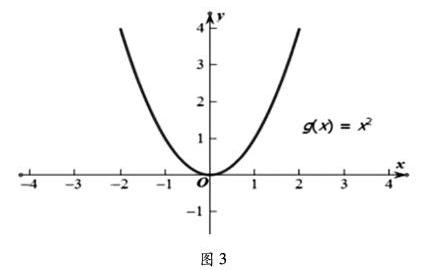
問題1：你能描述一下函數y=x2 圖像（圖3）的升降規律嗎？

生1：圖像在y軸右側是上升的，在y軸右側是下降的。

評析：讓學生描述函數y=x2圖像的升降規律，從觀察具體函數圖像為切入點提出這一基本問題，符合中職生數學思維水平，遵循數學思維發展從具體形象出發。問題是數學思維的起點，從基礎問題出發能激活學生原來已經習得的數學知識，進一步激發學生學習函數單調性的好奇心和興趣。

（三）感性認識增（減）函數

問題2：函數y=x2的圖像在y軸右側（左側）是呈上升（下降）的趨勢，那怎樣利用自然語言描述這種“上升”呢？

師：也就是在特定的范圍內，應變量y與自變量x的變化關系如何描述？

生1：函數圖像在y軸右側是上升的趨勢可以描述為：當x>0時，應變量y隨自變量x的增大而增大。

生2：函數圖像在y軸左側是下降的趨勢可以描述為：當x<0時，應變量y隨自變量x的增大而減小。

評析：學生在教師的引導下，根據當前的問題去調動、激活以往的經驗、知識，以融會貫通的方式對學習內容進行重新組織，在解決問題中，發生思維的碰撞。

（四）理性分析增（減）函數

問題3：如何用符號語言描述這種“上升”或“下降”呢？

師：引導學生發現在（0，+）上，任意改變x1，x2的值，只要當x1

在（-，0）上，任意改變x1，x2的值，只要當x1x22。

評析：教師科學設問，學生經歷從“圖像”到“自然語言”最后“符號語言”三個梯度的體驗，問題層層深入引導學生逐步深入思考。在問題解決的體驗過程中，學生數學思維的廣度和深度隨之擴展，進而有效地激發學生抽象思維的發展，逐漸搭建數學思維能力。隨后再給出增（減）函數的形式化定義，學生經歷定義的形成過程，對定義的理解起來相對輕松，對幫助學突破難點有一定的作用。

（五）實際應用，發展提升

課堂例題及練習主要從兩個方面設計，一方面是給出具體的函數圖像（分有限區間及無限區間兩類），確定函數的單調區間;另一方面是給出較簡單函數的解析式（如一次函數f（x）=3x+2），請學生利用定義證明函數單調性的題目，最后引導學生總結解題步驟，其目的仍是幫助學理解函數單調性的含義，但根據中職生的知識基礎及認知能力不宜成為重點。

（六）反例的獨特作用

問題4：對于特定的兩個x1，x2的值，當x1

生1：這個符合了增函數的定義，必然成立;生2：在函數y=x2中，也有當1<2時，有12<22，結果成立;生3：在函數y=2x中，也有當-2<5時，有-4<10，結果成立;

……

也有提出反對的意見：生3：在函數y=x2中，也有當-3<2時，卻有（-3）2>22，結果不成立;更有學生舉出反例：生4：在函數f（x）=-1x中，當-1<1時，卻有f（-1）>f（1），結果不成立;

師：因此，在理解函數單調性的定義中，我們必須強調“任意”二字。任意性指的是兩個自變量x1，x2的任意性，不能是給定的兩個。

評析：課堂的精彩源于學生的即興討論。通過老師有意義的設問，對接點在于“任意”兩字，全班學生的討論、舉例論證，學生會有一種豁然開朗的感覺，從而可以幫助學生深刻、準確地把握和理解單調性定義。所以，在課堂的教學中，教師如能充分地信任學生、不低估學生，學生的思維潛力將無限，課堂更加精彩。

三、教學思考

在中職數學的常規教學中，教師根據學情設計有意義、有梯度的問題，能有效激發學生發生思考，從而促進學生數學思維能力的發展，促使學生良好的思維品質的形成。

1.微課設問，激發思維碰撞

微課是一種教學輔助手段，它是一個教學載體，而“問題”是核心。在本課的教學中，課前以微課學習引領為手段，課中以問題驅動引領為主線。“微課”是推送給學生讓學生課前學習，實際上是一種帶有老師講解的預習，學生可以有時間、有空間，反復推敲、琢磨重點與難點問題。課堂是師生交流、互動、探究的重要場所，它為學生在“微課”學習中遺留下的一些不理解的知識提供了一個重要的解決問題的契機。因此，結合教學目標在學生的最近發展區設計恰當的“問題”又成為備課的關鍵。課堂上引領學生以“問題為中心”開展討論、交流，激起認知沖突、產生思維的碰撞，培養學生的思維能力，這才是課堂教學所追求的目標和方向。

2.問題引領，活躍思維能力

（1）問題引領學習，體驗概念的生成過程

在《函數的單調性》課堂教學過程中，教師利用y=x2圖像的變化趨勢的問題點開門見山引入，引導學生獨立思考。再過渡到數學的自然語言及數學的符號語言描述自變量x與因變量y的變化關系，最后給出增（減）函數的形式化定義。通過對問題的層層深入的解決，學生學習的成就感得以滿足，這種感受會促使學生繼續利用已有的知識去思考探索新知識，在探索中體驗和領悟。

（2）問題引起質疑，創造課堂的最高境界

筆者的理解，課堂互動的最高境界是思維的碰撞，也是課堂上教師鼓勵學生質疑，有學生不同的討論聲音，這樣的課堂才有生機和活力。

基于問題學習的《函數單調性》教學中，依托課前微課設疑，課中問題貫穿整個教學始終，以問題激活學生的數學思維，關注學生數學思維的參與，學生的數學思維遵循從具體思維到抽象思維的發展規律，最后到達辯證思維的體驗過程。總的來說，教師有意義地設計階梯問題，將數學思維訓練貫徹到常規課堂教學中，達到幫助學生逐漸形成良好的思維品質的目的。在“潤物細無聲”中，希望學生能在以后的學習中學會運用數學思維去解決問題，最高的層次乃是在生活中，具有數學思維，遇到問題能勇往直前地解決問題，這恰恰就是學習數學的最大的價值。

[本文是廣州市教育科學規劃2016年度立項課題：中職《數學（基礎模塊）》微課資源建設與應用的研究（課題編號：1201554663）的研究成果。]

責任編輯朱守鋰