全球定位系統基線解算病態問題的研究

代正嬌　邊倩倩　趙佶　王嘉祥　李育紅

摘要：自經典的最小二乘法（LS）被證明可以獨立應用于GPS數據的分析之后，最小二乘法便成為GPS數據處理過程中應用頻率較高的方法之一。但在 GPS快速定位等空間數據采集技術的迅速發展下，測量手段不斷提高，數據量迅速膨脹，數據之間的相關性越來越強，如果仍采用經典的 LS估計方法，必然會影響平差結果，導致結果精度偏低。因此，分析平差病態問題的形成原因和診斷度量方法，選擇更有效的方法來獲取準確的結果是處理GPS數據過程中重中之重的事。

關鍵詞：GPS雙差模型;病態性;有偏估計;嶺跡法;截斷奇異值

中圖分類號：TP311 ? ? ? ?文獻標識碼：A

文章編號：1009-3044（2019）14-0207-03

1 緒論

1.1 選題依據

隨著測量技術的快速發展，測量方法不斷完善，對定位信息及時性的要求也越來越高，但平差系統的病態性問題也越來越廣泛，使得 LS估計性質顯著變壞， LS估計值和真值相差太大，嚴重影響測量結果的精度，因此，必須找到更為有效的方法消除或削弱平差系統的病態性，以得到更為精確、可靠的平差結果。

對于GPS測量而言，具體的平差問題存在許多內部原因，例如控制點位置，參數確定等。 因此，在尋找病態性問題的形成規律時，必須分析產生病態的具體原因，分析應用和理論中的存在的病態問題。尋找更科學合理的解決方案，提高GPS測量站點坐標的準確性、可靠性和解算效率。

1.2 本文主要研究內容

解算成果受GPS測量平差系統病態性的影響越來越嚴重，為了解決這一難題，本文主要以當下 GPS研究的現狀和已有的結論為基礎，確立研究的主要內容如下：

（1）從實際的測量數據出發，歸納分析測量平差系統中法方程的病態問題產生的原因，并研究其診斷與度量方法，然后比較分析了 GPS相對定位觀測方程的三種模型各自的特征，確定本文所要采用的模型;

（2）著重研究有偏估計法和病態模型直接解法在平差病態問題中的應用。重點分析嶺估計與部分嶺估計在解決病態性問題上的優點;針對有偏估計中確定嶺參數這一難點對嶺跡法和 L-曲線法進行深入剖析;最后分析截斷奇異值法和修正奇異值法在解決病態性問題上的實用性和各自的差異性;

（3）用LS估計對獲取的GPS數據進行解算獲得平差坐標，然后以截取的少量歷元數據為基礎數據，將LS估計、有偏估計法和病態模型直接解法運用到平差系統雙差模型的解算中，并根據其解算結對比分析各類方法的有效性和優越性，

（4）對本文的工作做一下總結，并且明確下一步研究工作。

2 GPS測量誤差及相對定位觀測模型

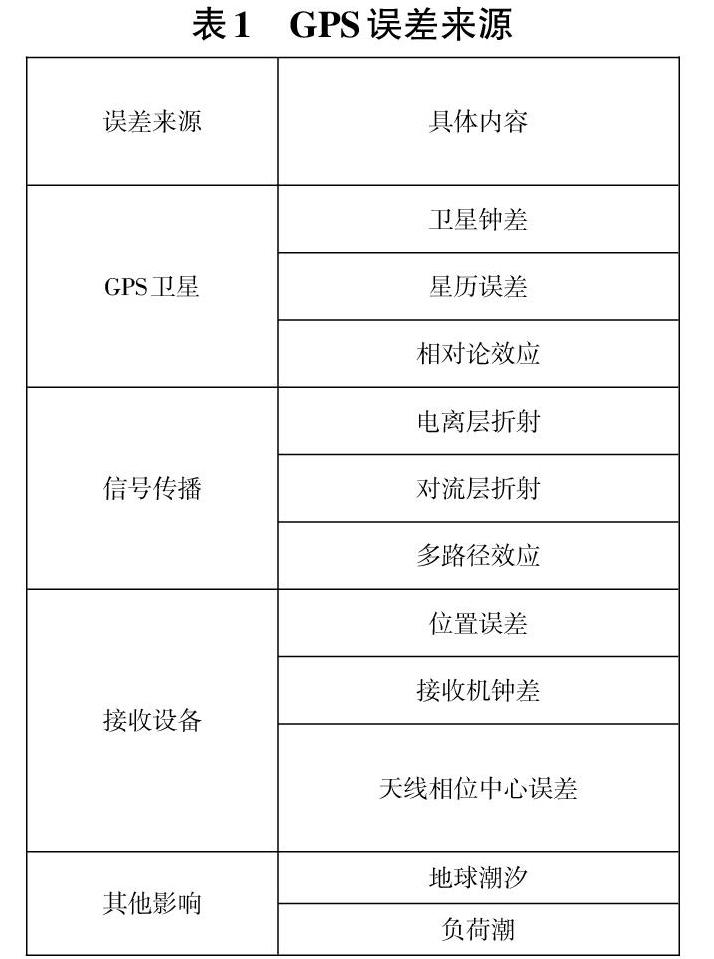
2.1 GPS測量的誤差來源

在GPS測量中，眾多要素造成了測量的精度降低。影響GPS定位精度的主要誤差包括GPS衛星、衛星信號傳播以及接收設備。 具體內容如表1所示。

另外，由觀察人員本身和觀察環境引起的誤差也以矩陣的形式干擾解算結果。

2.2 GPS相對定位觀測方程的確定

假如安置在某一個測站的GPS接收機，對GPS衛星進行同步觀測，則觀測方程為：

式中，[?]為相位觀測小數，[R]為接收機到衛星的真距離，[τ]為接收機鐘差，[N]為相位整周模糊度，[σ]為信號通過對流層和電離層的延遲改正，[（XS，YS，ZS）]為衛星瞬時地心坐標，[（XP，YP，ZP）]為接收機的地心坐標。

GPS相對定位觀測方程進一步推導出常用的三種形式：單差、雙差以及三差。 對三種模型進行綜合分析后，確定了在實際工作時采用的模型。其結果如表2所示：

從表2可以看出，單差觀測方程觀測量之間沒有相關性，但未知參數過多;三差觀測方程消除了衛星軌道誤差等大多數的未知參數，但由于三次作差使得觀測量之間相關性過強，解算結果精度變差。最后，在實踐應用時決定選用雙差模型進行解算。

3 GPS測量平差系統中的病態問題

3.1 測量平差模型的病態性

3.1.1 病態性擾動理論

自1829年高斯創立最小二乘法以來，特別是高斯-馬爾可夫定理證明了LS估計在線性無偏估計類中具有最小方差等優越性之后，使得LS估計被普遍應用于GPS數據處理中。然而在實際應用中LS估計并不適合于任何情況，當系數矩陣出現復共線性時，即陣的列向量存在近似相關性，此時平差模型出現病態問題，使得LS估計的精度很差，解算成果并不可靠。

因此，要想解決平差系統中出現的病態問題，首先要知道什么是病態問題？病態問題的一般定義是：原始數據的微小誤差對解算結果有顯著的影響，則該平差系統是病態的，反之系統是良態的。由此可知，病態性反映的是平差系統的抗干擾能力。

3.1.2 病態性與復共線性

復共線性是指矩陣中存在某些數據列可以互相近似線性表示。研究表明：復共線性是病態性存在的主要條件，復共線性存在，病態性一定存在。但復共線性不等于病態性。因為，病態性是平差系統本身的一種屬性，而且平差系統病態的原因是由多方面因素造成的，復共線性僅僅是其中的一個原因。但是在測量中，一般模型的建立通常是通過公式得到的線性系統，因此對于平差系統而言，可以認為復共線性等于病態性。

3.2 GPS測量平差系統病態性原因

減弱甚至消除平差系統病態問題的前提就是要正確分析病態性的形成原因。實踐表明，由于眾多因素的影響參數求解時的結果會產生病態方程組，概括起來導致了系統病態性的因素有如下幾種：

（1）參數過度化

參數過度化導致的病態問題的主要體現在兩方面：1）參數本身的錯誤。選擇了錯誤的參數意味著設計陣中的一些數據列和其他數據列存在一定的相關性，即這些參數不但沒有增加新的獨立信息反而干擾了其他參數，造成設計陣的均方誤差過大; 2）未知參數過多。一個參數有可能受多個變量的影響，同時，一個變量可能影響多個參數，在這種情況下過多的參數帶來了過度參數化，由這些參數建立的模型必然會復共線性，進而造成平差系統病態。因此，選擇適當的模型是非常重要的。

（2）觀測信息不足

在實際中獲取 GPS數據的外業環境有時會受客觀因素的影響，使得我們處在的不利的位置，造成觀測結構不合理，數據采樣存在一定的局限性，觀測信息不足等問題，使得觀測矩陣的列向量存在復共線性，矩陣從實測的GPS數據中無法獲得準確結果，從而產生病態性。

（3）數值計算

在用計算機處理數據時存在數據的舍入誤差同樣是不容忽視的，如果計算方法不能很好地控制舍入誤差的增長也可能導致結果失真。大量研究結果表明：不同的算法對同一個問題的解算結果有著很大的差異。因此，對于一個具體的平差問題來說選取合適的算法提高數值的穩定性、減少誤差的積累和傳播是非常重要的事。

3.3 GPS測量平差系統病態性的診斷與度量

無論在理論研究還是實際應用上，病態性的診斷和度量一直都是平差系統中非常重要的環節。病態性診斷的主要目的是判別系統是病態的還是良態的。如果系統是良態的，那么LS估計仍然是一個好的方法;反之，如果系統是病態的，只有正確認識到病態性形成的原因，才能確定具體的診斷和度量方法，進而選擇合適的處理方法。

截至到現在已經有十幾種診斷方法不斷被提出。通過比較幾種較常用的診斷方法的異同，進行歸納整合形成表3：

結合表3的內容，針對特定的問題選擇不一樣的診斷方法，對解決平差系統病態性問題有重大意義。

4 有偏估計和病態平差模型直接解法

4.1 有偏估計方法

一般說來，參數估值與參數真值之間的差距越小越好，而均方誤差（MSE）反映的就是參數估計的準確程度。所以當系統存在病態性時，用MSE來反映估計方法的優缺點最為合適。

一般情況下，為了得到的無偏的估值我們經常使用經典的最小二乘法。但在平差系統存在病態性時，運用最小二乘法所得到的解算精度很差，所以選擇了新的估計方法即有偏估計進行平差解算。均方誤差準則表明，在解決模型病態時有偏估計方法比LS估計更有效，運用有偏估計獲得的估值更精確、數值更穩定。

在有偏估計類方法中使用頻率較高的有針對法矩陣提出的嶺估計以及由嶺估計衍生出的部分嶺估計、廣義嶺估計等方法。這些方法在很大程度上解決了平差系統的病態問題，本文主要研究了嶺估計法和部分嶺估計法。

4.1.1 嶺估計與部分嶺估計

4.2 嶺參數的確定

嶺參數的確定是為了運用有偏估計方法時可以獲得更準確的估值。因此，選擇均方誤差最小時的嶺參數k值是最優的有偏估計，所以嶺參數的確定是后期解算成果的優劣的關鍵所在。在過去十年中，眾多專家學者從不同的方向給出了一些確定嶺參數的方法，幾種常用的方法原理如表4所示。

從表4中可以得知，嶺跡法和L-曲線法都是利用圖像來確定嶺參數，缺乏必要的理論支撐，主觀隨意性較強。而其他方法都有確切的公式，可以運用合理計算來確定最優嶺參數，其中 HK法和 Q（ C）準則法都必須通過 LS估計獲得的部分參數來確定嶺參數， GCV法基于逐一排除原理得到參數估值，以均值最小為條件求得嶺參數，雖然理論上是可行但是實際操作中過于困難， 一般不采用。

4.2.1 L-曲線法

L-曲線法是在嶺估計的基礎上，以log[X]作為縱坐標[η]，log[AX-L]作為橫坐標[ξ]，選擇不同的嶺參數k，便得一系列點[（AX-L，X）]，將這些點擬合成一條曲線，最優的嶺參數k是該曲線的曲率最大的點所對應的值。因為擬合后的曲線形狀近似“L”，故稱之為L-曲線法。

4.2.2 嶺跡法

嶺跡法主要步驟是：首先求出參數的嶺估計，然后將嶺估計公式中的各個分量作為k的函數，在紙上將函數圖形畫出，此函數圖形稱為嶺跡。這種方法的優點是直觀、簡單，但缺乏嚴格的理論根據，k值的確定具有一定的主觀隨意度，但由于其應用時間久遠，至今仍然被采用。

4.3 病態平差模型直接解法

包括嶺估計在內的各類有偏估計能夠減弱平差系統中法方程矩陣的病態問題，但對于設計陣的病態問題卻沒有作用，難以保證解決病態問題的程度。在平差系統中，如果降低誤差方程系數矩陣的病態性，法方程矩陣病態性也會隨之降低，從而獲得更接近于真值的參數估值。病態模型的直接解法顧名思義就是直接對相對定位觀測方程的系數矩陣進行解算來得到參數值，近年來在處理平差病態性問題中應用較為廣泛。

病態模型的直接解法中應用較為廣泛的幾類解法的原理如表5所示。

在病態模型直接解法中，截斷奇異值可以直接忽略相對小的奇異值，而修正奇異值是將全部或者部分奇異值進行修正。這兩種方法均可以提高參數的精度和可靠性，從而解算得到更為精確的值。截斷奇異值一般應用于奇異值呈“階梯狀”分布的病態矩陣，而修正奇異值應用在奇異值呈均勻分布的病態矩陣中的效果會更好。

5 總結與展望

5.1 總結

本文對于 GPS相對定位觀測模型中出現的病態性問題，從觀測模型的特征、誤差產生原因以及病態性診斷和度量方法等多方面進行研究、分析與總結，然后重點研究歸納了有偏估計及病態模型的直接解法解決平差系統病態性的主要原理與具體方法，并對有偏估計中較常用的嶺估計、部分嶺估計，以及確定嶺參數的嶺跡法和 L-曲線法進行具體分析。除此之外，重點研究了病態平差模型直接解法的截斷奇異值法和修正奇異值法。最后將研究成果應用到處理GPS數據中，解決了由于LS估計造成解不穩定的問題，并證明了有偏估計和病態模型直接解法在削弱和消除病態問題上的有效性和優越性。

5.2 下步研究工作的設想

盡管本文對平差系統病態性問題進行了一些研究，并獲得了一些結論，但是由于平差系統的復雜性，以后還有很多問題等待解決如下：

（1）將測量結果和病態問題緊密結合進一步分析病態性的實質，對更好解決病態問題有重要影響;

（2）進一步研究有偏估計和病態模型直接解法中各類方法的實用范圍和適用條件;

（3）本文主要是對線性系統的病態問題進行研究，對于非線性病態問題的分析也是下一步研究的重要方向。

【通聯編輯：朱寶貴】