國家教師資格考試“數(shù)學學科知識與教學能力”試題研究

潘騰　胡啟宙　孫慶括

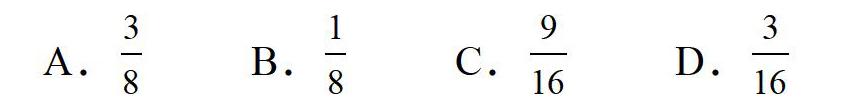
十年樹木，百年樹人，強國必先強教，而高素質的教師隊伍是教育強國的必要保障.2011年起，根據(jù)《國家中長期教育改革和發(fā)展規(guī)劃綱要（2010-2020年）》第十七章第五十五條的指示：“健全教師管理制度，完善并嚴格實施教師準入制度，嚴把教師入口關，制定教師資格標準”[1]，教育部啟動中小學教師資格考試改革，教師從業(yè)資格證書的獲取途徑從主要強調學歷達標的地方自主考試，轉變?yōu)樽⒅貙W科素養(yǎng)、教學能力的國家統(tǒng)一選拔考試[2].中學數(shù)學教師資格筆試部分增設“數(shù)學學科知識與教學能力”科目，通過對數(shù)學學科知識、中學數(shù)學課程與教學知識的全方位考查，提高數(shù)學教師行業(yè)準入門檻，促進教師隊伍的專業(yè)化發(fā)展.

自2013年《中小學教師資格考試暫行辦法》頒布實施以來，師范生畢業(yè)直接拿證的特權逐漸被取消，需要和非師專業(yè)考生一同參加國家統(tǒng)一命題考試，這樣才能獲得教師資格證書.相較于“綜合素質”、“教育知識與能力”兩門公共基礎課，“數(shù)學學科知識與能力”一科的通過率是最低的，成為不少師范生從教的攔路虎，也是當前師范教育培養(yǎng)模式轉型的關鍵所在.但由知網(wǎng)的檢索結果可知，已有研究多集中從國家政策、試題命制的宏觀層面分析資格考試，從學科視角審視“數(shù)學學科知識與教學能力”試題的高質量文獻卻不多，主要研究者有郭玉r峰[2.5]、趙軒[3，4]、鄭毓信[6，7]、段志貴[8]等.鑒于數(shù)學學科的重要地位，本文參照近5年的10份試卷，針對2018年3月份的“初中數(shù)學學科知識與能力”試卷進行整體分析和典型例題評析，以期探尋資格考試的命題特點與考試導向，為師范院校數(shù)學課程改革、考生備考提供參考和借鑒.

1 試卷總體分析

1.1 試卷結構

試卷是以《中小學教師資格考試大綱（試行）》（以下簡稱《考綱》）為依據(jù)，檢測考生的學科基礎知識與教學基本技能，注重考查應用知識和方法分析解決問題的能力，凸顯全國統(tǒng)一考試的甄選功能.

歷年試卷結構相同，題型穩(wěn)定，主要考查數(shù)學學科專業(yè)知識和課程與教學論的知識.試卷由6種題型組成：8道選擇題，每題5分;5道解答題，每題7分;l道解答題，10分;l道論述題，15分;l道案例分析題，20分;l道教學設計題，30分.總分150分，考試時間為120分鐘，考試形式是閉卷.

1.2 試卷內容

由上表可知，試卷在數(shù)學學科基礎知識有66分，占比44%，略高于考綱要求的41%，且考查內容多為高等數(shù)學.在中學數(shù)學課程與教學論知識部分有84分，占比56%，略低于考綱要求的59%，且多與初中數(shù)學知識結合考查.考試內容大體上與《考綱》保持一致.

1.3 試卷特點

1.3.1保持整體平穩(wěn)，規(guī)避命題模式

與近5年試卷相比，2018年試卷在題型設置、分值比例、內容分布等整體結構和難易程度方面保持相對平穩(wěn).但在保持穩(wěn)定的同時，選擇題全方位考查學科知識、課程知識、教學知識等基礎內容.簡答、論述、案例分析等大題設問方式豐富多彩，考查角度新穎獨到，規(guī)避命題的模式化.

1.3.2立足學科基礎，注重數(shù)學素養(yǎng)

“傳道、授業(yè)、解惑者，師也”，扎實的專業(yè)知識與技能是為師授業(yè)的前提.試卷立足于高等數(shù)學中最基本知識點、性質及其相關定理的應用，考查運算求解、空間想象、推理論證等數(shù)學能力，兼顧數(shù)學思想方法、數(shù)學史等數(shù)學文化素養(yǎng).

1.3.3注重教學實際，凸顯導向功能

試題注重理論與實踐的結合，不拘泥于題型，采用多樣化的教學情境素材，以中學課程體系中最核心、具有貫通性的基本知識點為依托，考查新教師在實際教學中應用教學理論的綜合能力.此外，教師資格考試具有育人導向、能力導向、實踐導向和專業(yè)化導向功能，充當著新時期對一名合格數(shù)學教師新要求的風向標.

2 典例分析

2.1 數(shù)學學科知識

數(shù)學學科知識包括大學專科數(shù)學專業(yè)基礎課程、高中數(shù)學課程中的必修內容和部分選修內容以及初中數(shù)學課程中的內容知識.考試更為注重與中學數(shù)學有縱向銜接的高等數(shù)學知識的考查，關注考生的數(shù)學思維能力、數(shù)學解題能力、數(shù)學文化意識，

例1（題1）下列命題不正確的是（ ）

A.有理數(shù)對于乘法運算封閉

B.有理數(shù)可以比較大小

C.有理數(shù)集是實數(shù)子集

D.有理數(shù)集是有界集

評析 本題考查的是有理數(shù)集的性質，有理數(shù)集是貫穿初、高等數(shù)學的集合概念.雖在中學階段僅涉及有理數(shù)的四則運算，但教師則需從高觀點下看待初等數(shù)學，將高數(shù)中某些概念和理論與中學數(shù)學的相應原型、特例結合起來，準確把握中學數(shù)學的本質與關鍵.[1]答案為D.

例2（題5）邊長為4的正方形木塊，各均涂成紅色，將其鋸成64個邊長為1的小正方體，并將它們攪勻混在一起，隨機抽取一個小正方體，恰有兩面為紅色的概率是（ ）

評析兩個面都有顏色的小正方體應處于棱上（除過頂點處），而每條棱有2塊小正方體，因有12條棱，故共有24塊小正方體，因此取到兩面有顏色 與立體幾何結合考查，體現(xiàn)命題的創(chuàng)新，難度適中.此外，選用常見的問題情境為實際載體，以排列組合和概率統(tǒng)計的基本知識為工具，考查分類與整合、化歸與轉化、或然與必然思想運用的試題，也是資格考試的常見形式，如2015年下半年第II題，2017年上半年第11題.

例3（題14）設f（x）是R上的可導函數(shù)，且f（x）>0.

（l）求Inf（x）的導函數(shù);（4分）

（2）己知f1（x）-3x2f（x）=0，且f（0）=1，求f（x）.（6分）

評析 本題以解答題的形式考查了復合函數(shù)求導問題，具有一定區(qū)分度.函數(shù)求導問題一貫是解答題的考查熱點，如2017年上半年的積分函數(shù)求導，2016年下半年的微分中值定理的證明題.該題較好地考查了大綱所要求的計算能力、邏輯推理能力、綜合分析能力.

例4（題7）下面不屬于“尺規(guī)作圖三大問題”的是（ ）

A.三等分任意角

B.作一個立方體使之體積對于立方體體積的二倍

C.作一個正方形使之面積等于已知圓的面積

D.作一個正方形使之面積等于己知正方形的面積二倍

評析 本題考查的是古希臘三大作圖問題的具體內容，屬于簡單的識記層次.近年來，數(shù)學文化的教育價值愈發(fā)受到重視，HPM成為研究熱點.除去對知識與技能層面的要求，中學教學更關注如何將數(shù)學思想方法、數(shù)學文化、數(shù)學情感等有機融入課堂，培養(yǎng)學生的科學精神、創(chuàng)新能力、文化價值.答案為C.

2.2 中學課程與教學論

中學數(shù)學課程知識部分側重于對《課標》的性質、基本理念和相關教學內容的考查，更關注《課標》理論是如何運用到具體課程實施中的.教學知識與技能部分側重于檢測考生教學設計、教學實施和教學評價等三個維度的教育教學能力.

例5（題13）筒述你對《義務教育數(shù)學課程標

準（2011年版）》中“探索并證明三角形的中位線定理”這一目標的理解.

評析 本題考查三角形中位線定理的一條具體教學目標，有利于區(qū)分不同考生對中學課程標準的掌握程度和學科專業(yè)素養(yǎng)，體現(xiàn)了選拔性.《課標》是國家制訂的指導課程實施的綱領性文件，也是教師教學的兵法，深刻把握教育理念是教師上好一堂課的前提.因此，師范生在解讀課程標準時，既要關注政策層面，更要關注課標理念的具體運用.

例6（題l5）《義務教育數(shù)學課程標準（2011年版）>>在教學建議中指出應當處理好“面向全體學生與關注學生個體差異的關系”，論述數(shù)學教學中如何理解和處理這一關系.

評析 教學活動應努力使全體學生達到目標的基本要求，同時要關注學生的個體差異，促進每個學生在原有基礎上獲得發(fā)展.這也體現(xiàn)了“人人學有用的數(shù)學，人人掌握數(shù)學，不同的學生學習不同的數(shù)學”的大眾數(shù)學的教育理念.有別于“教育知識與能力”科目的考查，本題更關注的是如何在數(shù)學教學中理解和處理這一關系.

例7（題16）在有理數(shù)運算的課堂教學片斷中，某學生的板演如下：

針對該學生的解答，教師進行了如下教學：

師：請仔細檢查演算過程，看是否正確無誤？

生：好像正確吧！

師：對于這個，你是怎樣想的？

1

生：負1減5，不對，是負1負—的和，不對，

5哎呀！老師，我不會了.

問題：（1）請指出該生解題中的錯誤，并分析錯誤的原因;（10分）

（2）針對該生在解題中的錯誤，教師呈現(xiàn)如下兩道例題，并板書了解答過程：

請分析例題l、例題2中每一步運算的依據(jù).（10分）

評析 本題是以有理數(shù)運算為背景的案例分析題，分值權重較大.雖考查內容為基礎知識，落點較低，但形式和立意新穎，且案例材料真實鮮活，具有很強的實踐性與代表性.一方面，綜合考查了考生在教學實際中分析和解決問題的能力，另一方面也是出于對考生能否臨場應變、最大化利用生成的錯誤資源，發(fā)揮課堂最大功效的教育機智的要求.

例8（題17）加權平均數(shù)可以刻畫數(shù)據(jù)的集中趨勢，《義務教育數(shù)學課程標準（2011年版）》要求“理解平均數(shù)的意義，能計算中位數(shù)、眾數(shù)、加權平均數(shù)”，請完成下列任務：

（l）設計一個教學引入片段，體現(xiàn)學習加權平均數(shù)的必要性;（12分）

（2）說明加權平均數(shù)的“權重”含義;（6分）

（3）設計一道促進學生理解加權平均數(shù)的題目，說明具體的設計意圖.（12分）

評析 教學設計題是教師資格考試的特有題型，分值權重最大.數(shù)學教學設計是教學之前的規(guī)劃藍圖，是整個教學活動得以順利進行的基礎和保障.本題綜合體現(xiàn)了考試的實踐導向和專業(yè)化導向，優(yōu)秀師范生成長所需的是綜合教學能力的發(fā)展，而不是假性教學能力.第（l）、（3）小題的教學環(huán)節(jié)設計答案開放性很強，只要符合要求，均可得分.

3 總結與建議

總體上看，2018年上半年的初中試卷注重平穩(wěn)，強調應用意識與能力導向，在整體內容結構、試題設計、能力考查的層次要求等方面不斷完善，更顯科學化、規(guī)范化，顯現(xiàn)出新時代對學科知識與教學能力兼?zhèn)洹⒗碚撝R深厚、實踐能力突出的高素質數(shù)學教師的呼吁.

3.1 師范院校模式轉型

高校需與時俱進，改革不適宜的課程體系與評價制度，調整不恰當?shù)慕虒W方法與教學內容，注重理論與實踐相結合，加強對學生綜合素質的全方位培養(yǎng).如在高等數(shù)學系列課程上，更關注師范生數(shù)學能力與素養(yǎng)的發(fā)展，強調與初等數(shù)學的縱向本質聯(lián)系，從高觀點下看待初等數(shù)學;在教育理論系列課程上，更關注理論與教學實際的結合，使學生能夠真正地學以致用;在教學技能系列課程上，更關注師范生實際教學能力的提升，加強互動演練，定期舉辦說課技能大賽、微格教學比賽等實踐活動.

3.2 師范學生砥礪前行

師范生必須從“教書匠”的技能學習轉為“教育家”的能力成長，在日常專業(yè)課程學習中注重養(yǎng)成性

發(fā)展，以積極主動的狀態(tài)備戰(zhàn)教師資格考試.在備考時要勤學多思，把握大學數(shù)學的基礎知識，以及本體性知識的擴展和應用;認真研讀課程標準，能夠掌握并應用其指導自己的數(shù)學教學實踐;理解中學數(shù)學教學知識并習得教學相關能力，注重理論與實踐結合;深刻體會數(shù)學思想方法與文化價值，以便融會貫通、靈活運用.

參考文獻

[1]楊柳惠，陳清華，福建省中小學新任教師公開招聘考試中學數(shù)學試卷評析—一以2011.、2012年試卷為例[J].福建中學數(shù)學，2013 （02）：2-5

[2]郭玉峰，陳晨，王尚志.國家教師資格考試之“案例分析題”研究：含義、步驟及框架[J].數(shù)學教育學報，2015，24 （06）：13-17

[3]趙軒.注重能力考查推進專業(yè)化發(fā)展一中學數(shù)學教師資考試目標要求和試題特點及測評情況分析[J]，數(shù)學教育學報，2016 （06）：7-9

[4]趙軒，中小學教師資格考試數(shù)學學科教學能力考查研究[J].中國考試，2015 （06）：35-38

[5]陳瑩，郭玉峰，國家教師資格考試高中數(shù)學學科知識題研究：基于2012-2015年7套真題的分析[J].數(shù)學通報，2017，56 （11）： 12-18

[6]鄭毓信，數(shù)學教師資格考試“試題”的幾個思考[J].人民教育，2015（18）：57-60

[7]鄭毓信，從教師資格考試到教師專業(yè)成長[J].數(shù)學教育學報，2015，24 （06）：7-12

[8]段志貴，陳宇，合格初中數(shù)學教師學科教學知識研究[J]，數(shù)學教育學報，2017，26 （02）：35-40

（本文系2016年南昌師范學院教改課題《教師資格證及公開招聘統(tǒng)考背景下高師數(shù)學專業(yè)課程與教學改革研究》（課題編號JGKT-16-20）研究成果之一）