找到事物的另一面,實現巧妙的轉化
——以四邊形分類新秩序為例
江蘇省常州武進區盧家巷實驗學校 岳麗芬
讀過一個經典的佛理故事,名字叫《佛經對了,佛就笑了》,內容是一位禪師,懲罰寺院里一名不守清規的弟子,罰他面壁思過。墻壁上掛著一幅彌勒佛畫像,禪師給受罰弟子出了一道難題,也算是一次將功補過的機會,禪師隨手將畫像撕成很多碎片,讓弟子在一炷香的時間內拼完,按時完成任務就可以提前恢復自由,否則只能乖乖挨罰。
令禪師萬萬沒想到的是,不到一盞茶的工夫,受罰的弟子就拼完了畫像。禪師感到震驚和納悶,因為他是第一個破解難題,成功逃脫面壁懲罰的弟子,禪師急忙問其究竟。
弟子回答:“佛像背面是一行行用歐體正楷抄寫工整的佛經,是《法華經》中的一段,我背得滾瓜爛熟,只要把佛經還原了,彌勒佛畫像也就拼好了。”故事結尾有一句發人深省的話:“佛經對了,佛就笑了。”
單從考慮問題的智慧來說,這個弟子的做法的確出人意料,如果老老實實按照要求去做很難完成任務,可是這個弟子卻懂得變通,將原問題轉換成另一個問題,降低了難度,順利解決問題,也就是將一個復雜的問題(佛像的拼接)轉換成另一個簡單的問題(佛經的拼貼)。
這個哲理故事告訴我們轉化思維多么神奇和重要,在小學數學中,求圖形的面積時,轉化思維可以大顯神通。
一、接入轉化思維,重新分類定秩序
本文著重要講的是四邊形的面積及其分類,先說分類。在教材中,根據對邊平行的情況,可以將其分為三類:第一種是沒有對邊平行,第二種是只有—組對邊平行,第三種是兩組對邊都平行。分類情況如下圖:
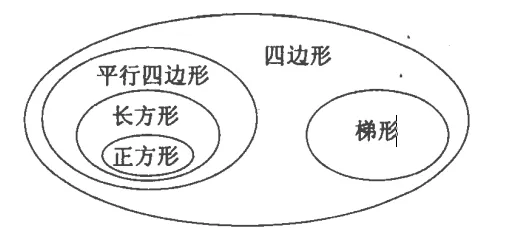
在這個分類中,四邊形被分為三大類:只有一組對邊平行的四邊形(梯形)、兩組對邊都平行的四邊形(平行四邊形),這是兩大類,空白處為一般四邊形,是小類,極易被忽略。在這種分類法里,極易讓人產生誤會:四邊形除了梯形就是平行四邊形,二者合并起來構成全部四邊形,其實這種分法欠妥。
在這種分類里,平行四邊形和梯形是并列關系,平行四邊形里又包含長方形,長方形里又包含正方形。
如果我們換種分法,另行設立分類標準——“有無對邊平行”,平行四邊形則被分為兩大類:1.沒有對邊平行;2.有對邊平行。在第2類里面又分很多小類,小類的細化就是不斷增加附屬條件,豐富內涵,縮小外延。如僅僅說明一組對邊平行,則為梯形;若梯形中的另一組對邊也平行,則為平行四邊形;若梯形的另一組對邊平行且有一個內角為直角,則為長方形;若梯形的另一組對邊平行且含有一個直角內角且鄰邊相等,則為正方形。
在這種分法下,平行四邊形屬于梯形的一部分,是一種比較特殊的梯形,換言之,二者不再是并列關系,而是包含關系。分類圖如下:
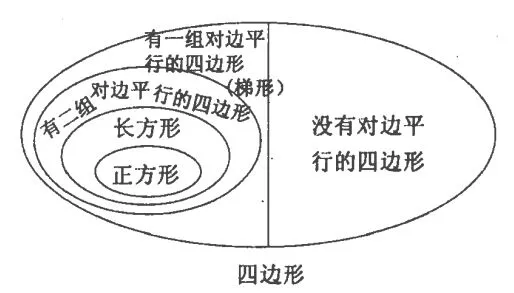
二、確立新的標準,重新表述縮外延
各種分類方法都有其合理性,那么這種分類的優勢在哪?
對照下列語句:
對于一個四邊形,假若有一組對邊平行,則為梯形;
對于一個四邊形,假若有一組對邊平行且相等,則為平行四邊形;
對于一個四邊形,假若有一組對邊平行且相等,還有一內角為90度,則為長方形;
對于一個四邊形,假若有一組對邊平行且相等,而且還有一內角是90度,此外發現鄰邊也相等,則為正方形。
可以發現,隨著對“梯形”概念內涵的拓寬,其外延在不斷縮小。這種一般到特殊的分類符合演繹推理的邏輯思維。
三、越過中間環節,一步到位求面積
在小學數學中,要求學生掌握各種四邊形面積的計算。
教材中對各種圖形的面積公式推導,包括三角形在內,都是從長方形開始的。首先規定各面積單位的原始定義,用數方格的方法,歸納出長方形的面積公式:長方形的面積=長×寬。
長方形的面積公式出爐后,繼續轉化,以長方形面積公式為基礎,用割補法將平行四邊形變換為長方形,推出平行四邊形面積=底×高。梯形和三角形也是這樣,都是轉化為平行四邊形后,再來推導。
在四邊形的新分類法中,可以先由長方形推出梯形面積,因為其他四邊形和三角形都可以視為特殊的梯形,所以在梯形為轉化標準的情況下,梯形面積公式可以演變為其他圖形面積公式。
那么梯形的面積公式從何而來呢?可以按照教材安排,先將梯形轉化為平行四邊形,再將平行四邊形轉化為長方形,導出其面積公式,也可以一步到位,將梯形直轉成長方形,然后推導面積公式。如圖1:
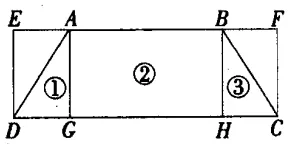
圖1
已知梯形ABCD的上底長為a,下底長為b,高為h。求面積。如圖,將梯形分成①、②、③三大區塊,各區域面積為:

觀察可知:DG=HC。
所以S1+S2+S3
=DG×h÷2+a×h+HC×h÷2
=h×(DG+HC)÷2+ah
=h×(b-a)÷2+ah
=bh÷2-ah÷2+ah
=bh÷2+ah÷2
=(a+b)h÷2
針對圖2,圖3這兩個梯形,可以如法炮制。
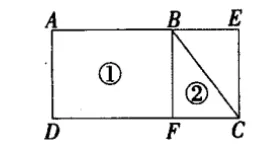
圖2

圖3
以梯形面積公式為母本,根據平行四邊形的上下底相等的特殊性,推導其面積為(a+a)×h÷2=ah。
對于三角形的面積公式,也可以通過梯形面積轉化而來。如圖4,梯形ABCD中,上底長為a,下底長為b,高為h。
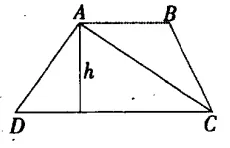
圖4
設B點為動點,沿上底向左移動,行至A點后停止運動,此時梯形上底縮短至一個點,長度變為0。梯形同時變形為三角形,代入公式有:S三角形=(0+b)×h÷2=bh÷2。
不同的思路,會產生不同的分類標準。所謂轉化思想,其實就是轉換一種思路,最終達到同樣的目標。本文僅從四邊形分類與面積重新推導來闡述,紕漏之處還請專家同行批評指正。

