有限元法解一維桿單元、熱傳導和流體流動問題的相似性比較

王銘明 胡圣明 于浩 汪晨

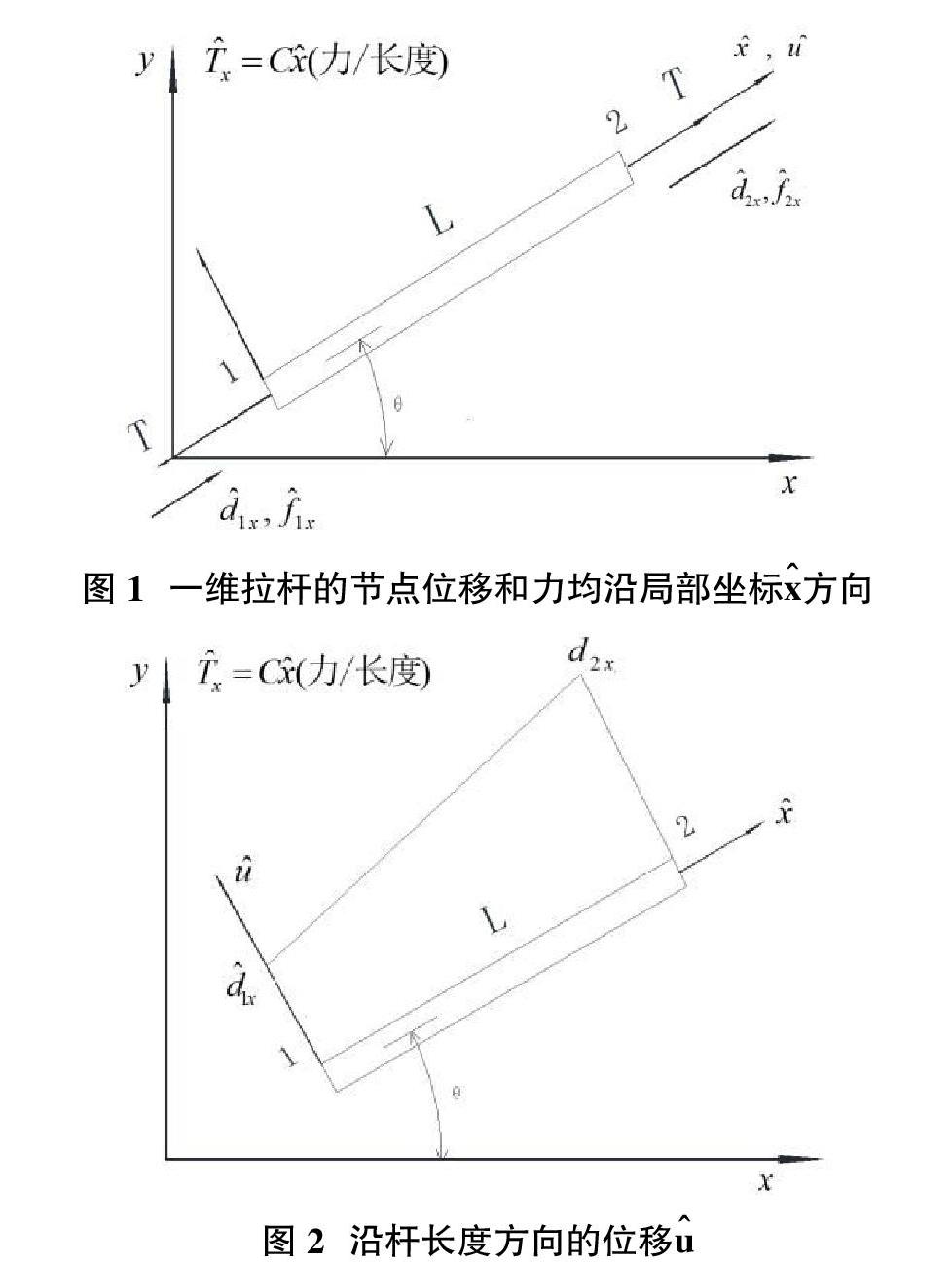
摘要：本文通過對求解一維桿應力的有限元剛度矩陣及其方程的推導，并根據類比的方法，延伸推導了一維熱傳導和流體運動的有限元求解過程。通過比較分析發現，采用有限元法解決上述三種問題的基本原理完全相同，推到出的剛度矩陣及方程也有很大的相似性，可以用相同的方法推廣到二、三維的情況。

Abstract： This paper deduces the finite element solution process of one-dimensional heat conduction and fluid motion by deriving the finite element stiffness matrix and its equations for solving one-dimensional bar stress and according to the analogy method. Through comparative analysis， it is found that the basic principles of solving the above three problems by using the finite element method are exactly the same， the stiffness matrix and the equations that are pushed out have great similarities， and it can be extended to the second and third dimensions by the same method.

關鍵詞：一維桿;熱傳導;流體運動;有限元法;剛度矩陣

Key words： one dimensional rod;heat conduction;fluid motion;finite element;stiffness matrices

中圖分類號：V231.1+3 ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?文獻標識碼：A ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?文章編號：1006-4311（2019）09-0152-04

0 ?引言

自上世紀40年代有限單元法[1]問世以來，隨著計算機科技的快速發展，很多學者將其廣泛地應用到各個領域，包括結構分析、熱傳導分析、流體運動分析、質量傳輸和電磁電位分析等方面[2]。

現今，有限元法已經發展的十分成熟，已經出現了很多大型商用有限元軟，如ANSYS、ABAQUS、ADINA、FLAC 3D等等。這些商業軟件使有限元法在工程應用中更加方便，也提高了高大復雜結構計算的可行性。因此，一些工程領域已經有限元法的力學分析寫入了相關規范，如《水電工程水工建筑物抗震設計規范》（NB 35047-2015）。

盡管采用有限元法解決許多不同領域的工程問題看似是無關的，但如掌握有限元的基本原理就會發現，用有限單元法求解這些問題時，都存在著一定相似性。

本文根據有限元的基本原理，列舉了一維的桿單元、熱傳導、流體運動的剛度矩陣及求解方程的推導過程，比較、分析、總結其相似性，使有限元法的基本原理更清晰，便于工程學者們學習及應用。

4 ?結語

本文對工程中最簡單的一維桿受力、熱傳導和流體運動的問題，應用有限元方法對其推導剛度矩陣及方程過程，通過比較分析發現在有限元求解上述問題時，在基本原理上完全相同，在應用上有極大的相似點。對工程界學習有限元及其應用有極大的幫助，可以觸類旁通地既快又好的掌握這種方法。本文雖然只是介紹了一維的有限元方法，但是工程學者也可以用本文的方法，接著將此推廣到二維、三維的情況。

參考文獻：

[1]王勖成.有限單元法[M].北京：清華大學出版社，2003.

[2]尹飛鴻.有限元法基本原理及應用[M].北京：高等教育出版社，2010.

[3]Daryl L.Logan（著），伍義生，吳永禮，等（譯）.有限元方法基礎教程（第三版）[M].北京：電子工業出版社，2003.

[4]Turner， M. J.， Clough， R. W.， Martin， H. C.， and Topp， L. J.， Stiffness and Delflection Analysis of Complex Structures[J]. Journal of the Aeronautical Sciences， 1956， 23（9）： 805-824.

[5]Martin， H. C. Plane Elasticity Problems and the Direct Stiffness Method[J]. The Trend in Engineering， 1961， 13（1）： 5-19.

[6]Oden. J. T. and Rippcrger， E. A. Mechanics of Elastic Structures （2nd ed.）[M]. McGraw-Hill， New York， 1981.

[7]Holman. J. P. Heat Transfer （8th ed.）[M]. McGraw-Hill， New York， l997.

[8]Zienkiewicz， O. C. and Cheung， Y. K. Finite Elements in the Solution of Field Problems[J]. The Engineer， Sept. 24.1965， pp： 507-510.

[9]Wilson， E. L. and Nickell. R. E. Application of the Finite Element Method to Heat Conduction Analysis[M]. Nuclear Engineering and Design， 1966， 4： 276-286.

[10]Emery， A. F. and Carson. W. W. An Evaluation of the USA of the Finite Element Method in the Computation of Temperature[M]. Journal of Heat Transfer. American Society of Mechanical Engineers， May， l971， pp： l36-145.