三維螺旋主纜懸索橋總體構(gòu)思

胥潤東

（中鐵大橋勘測設(shè)計院集團有限公司，湖北 武漢 430050）

0 引 言

受到D N A雙螺旋結(jié)構(gòu)的啟發(fā)，奧雅納（Arup）公司在新加坡設(shè)計了一座極具特色的雙螺旋人行懸索橋（Helix Pedestrian Bridge），如圖1所示。這座橋雖然外形是螺旋結(jié)構(gòu)，形成螺旋結(jié)構(gòu)的外層鋼管既有受拉部分也有受壓部分，其受力原理是一座桁架管橋，如圖2所示。因為造型奇特、充滿童趣，且與旁邊的公路橋形成了剛?cè)岵男Ч藰蚓坝^效果較好，已經(jīng)成為地標性建筑。

圖1 三維螺旋主纜懸索橋結(jié)構(gòu)簡圖（來自Arup官網(wǎng)）

如果允許橋面有一定的撓曲，且具備錨固條件，可嘗試將具有多根平行主纜的懸索橋一端或兩端反向進行旋轉(zhuǎn)，形成一種新型的懸索結(jié)構(gòu)，稱為三維螺旋主纜懸索橋（見圖3）。三維螺旋懸索橋傳力途徑明確，主纜完全受拉，是主傳力構(gòu)件，類似于普通懸索橋。空間螺旋的主纜使其具有一些特殊的力學特性。本文通過數(shù)值模型進行仿真分析，探索三維螺旋主纜懸索橋的基本力學特征。

圖2 Helix Pedestrian Bridge受力原理（來自網(wǎng)絡(luò)）

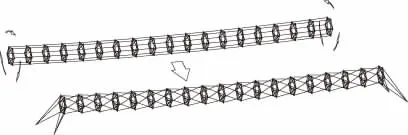
圖3 三維螺旋主纜懸索橋結(jié)構(gòu)簡圖（未示人行道）

表1 懸索橋關(guān)鍵結(jié)構(gòu)參數(shù)

1 方案構(gòu)思和分析方法

選取某構(gòu)思的平行六主纜人行懸索橋方案作為研究對象，為了形成空間結(jié)構(gòu)，每隔一定距離作為一個節(jié)段，用節(jié)間片分割（見圖3）；其基本結(jié)構(gòu)參數(shù)見表1，節(jié)間片的構(gòu)造如圖4所示，節(jié)間片之間搭設(shè)人行道板，構(gòu)成基本結(jié)構(gòu)。嘗試每次扭轉(zhuǎn)增量為36°，共扭轉(zhuǎn)10次，達到扭轉(zhuǎn)角360°。相對應地建立11個數(shù)值模型，在每個主纜的端部施加20 t的水平分力進行主纜找形。

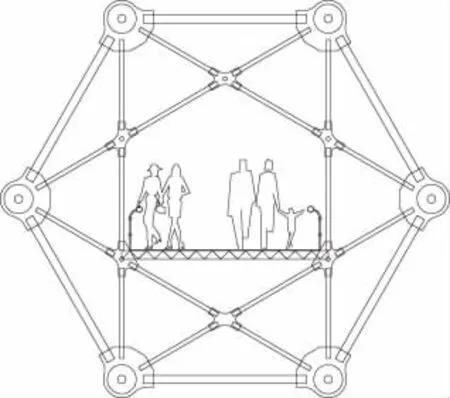
圖4 節(jié)間片結(jié)構(gòu)簡圖

扭轉(zhuǎn)過程中主纜逐漸彎曲，形成空間的螺旋結(jié)構(gòu)，主纜的無應力長度是在逐漸增加的；且主纜的扭轉(zhuǎn)過程中表現(xiàn)出了很強的大位移效應和幾何剛度變化。由于建模工作量很大，根據(jù)成熟懸索橋主纜找形和計算方法并參考了目前幾個新研究成果[1-6]，采用自編程序?qū)崿F(xiàn)了旋轉(zhuǎn)建模和計算自動化，并能輸出通用有限元模型進行計算復核。計算模型為桿系組合的魚骨模型。用三維梁單元模擬節(jié)間片，主纜采用考慮初張力的桿單元模擬，計算中疊加幾何剛度并考慮大位移效應。

本文選取了6根主纜和六邊形節(jié)間片作為研究對象，實際上只要主纜大于3根都可以匹配相應的節(jié)間片。本文節(jié)間片的外接圓半徑是8m。顯然，主纜數(shù)量少則橋上的視野透視性更好，主纜多則更可以體現(xiàn)結(jié)構(gòu)的美感。

2 節(jié)間片承受的徑向壓力特性

在三維螺旋主纜懸索橋成型過程中，由于平行的主纜同時轉(zhuǎn)動了相同的弧度，不會產(chǎn)生相互的擠壓力，所以沒有環(huán)向壓力；由于每根主纜都是平滑螺旋，也不會產(chǎn)生環(huán)向力。螺旋扭轉(zhuǎn)過程中，主纜的走向發(fā)生了改變，會帶來作用于節(jié)間片的壓力，這種現(xiàn)象主要是主纜力的徑向分力造成的。為了求解節(jié)間片徑向壓力與扭轉(zhuǎn)角之間的關(guān)系，選取任意相鄰的三個節(jié)間片作為研究對象（見圖5），僅顯示一根主纜，其他根受力類似。假定節(jié)間片的距離為d，主纜從A點出發(fā)，轉(zhuǎn)過β角后，到第二節(jié)間片的C點，假定C點在第一節(jié)間片外接圓上的投影為B。

圖5 節(jié)間片結(jié)構(gòu)簡圖

由于主纜豎向垂度的存在，ABC平面會不完全垂直于第一節(jié)間片，但其影響可以忽略。單獨選取ABC平面和OAB平面進行分析，如圖6所示。

圖6 節(jié)間片結(jié)構(gòu)計算簡圖

行間片的間距是d，假定AB兩點之間的距離是a，在ABC平面內(nèi)，力T在AB方向的分力為

在OAB平面內(nèi)，徑向力為TAB的分力：

投影長度a可由下式計算：

將投影長度a代入公式得任意一點的徑向力：

繪制節(jié)間片徑向壓力和主纜的扭轉(zhuǎn)角之間的關(guān)系如圖7所示。隨著扭轉(zhuǎn)角的增加，節(jié)間片壓力呈二次拋物線增長。

3 豎向和橫向剛度的敏感性

三維螺旋主纜懸索橋的力學特性復雜，由于螺旋形主纜的空間按復雜性和相互之間的關(guān)聯(lián)性，主纜的內(nèi)力也會隨著旋轉(zhuǎn)不斷變化，很難利用解析的方法推導結(jié)構(gòu)剛度。本文在數(shù)值模型的跨中施加豎直向下的80 kN的力，計算結(jié)構(gòu)的變形，作為豎向剛度比較的依據(jù)。計算結(jié)果匯總?cè)鐖D8所示。

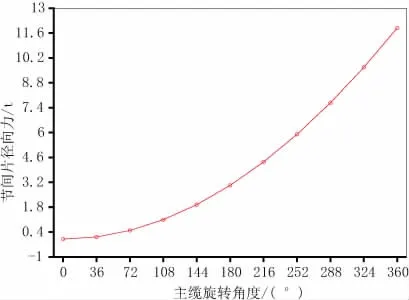
圖7 旋轉(zhuǎn)角和徑向力的關(guān)系

圖8 豎向撓度與扭轉(zhuǎn)角度的關(guān)系

從圖中可見，隨著扭轉(zhuǎn)角的增加，結(jié)構(gòu)的豎向剛度不斷增加。變形曲線類似于S形，說明隨著扭轉(zhuǎn)角的增加，結(jié)構(gòu)豎向剛度先增加后下降，扭轉(zhuǎn)角為288°時達到最大的豎向剛度，豎向變形值從217mm降低到136mm。跨中施加80 kN的橫向力，結(jié)構(gòu)的橫向變形如圖9所示。橫向變形曲線也類似于S形，結(jié)構(gòu)的橫向變形值從241mm降低到141mm。說明通過扭轉(zhuǎn)可以有效提高結(jié)構(gòu)的剛度。

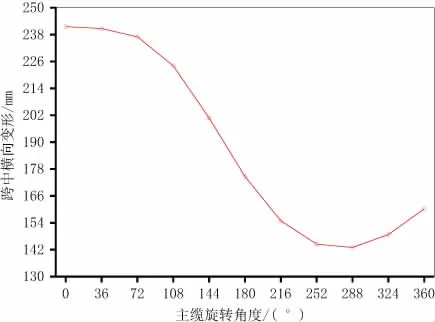
圖9 橫向變形與扭轉(zhuǎn)角度的關(guān)系

可以利用桁架模擬結(jié)構(gòu)狀態(tài)來解釋剛度增加的原因。結(jié)構(gòu)扭轉(zhuǎn)前是平行主纜，各個主纜均勻受力，結(jié)構(gòu)的剛度是各個主纜剛度的直接疊加。由于旋轉(zhuǎn)作用，使得主纜之間相互交叉和約束，形成了類似于空間桁架管橋效應，所以結(jié)構(gòu)的剛度會隨著扭轉(zhuǎn)角度的增加而逐漸增加。本例中扭轉(zhuǎn)角度達到288°時結(jié)構(gòu)剛度最大，繼續(xù)扭轉(zhuǎn)剛度反而會降低，這是由于當扭轉(zhuǎn)達到360°時，兩邊約束的節(jié)間片恰好重合，兩側(cè)主纜的變形協(xié)調(diào)，所以剛度反而稍有下降。

4 抗扭剛度的敏感性

不像普通懸索橋，扭轉(zhuǎn)引起三維螺旋懸索橋的變形要更復雜。因為扭轉(zhuǎn)使得一側(cè)增加螺旋而一側(cè)減少螺旋，這樣會引起一側(cè)加載而另一側(cè)卸載。主纜力的變化還會引起節(jié)間片的傾斜。本文在數(shù)值模型的跨中施加80 kN·m的扭矩，計算結(jié)構(gòu)的變形，作為抗扭剛度比較的參考。計算結(jié)果匯總?cè)鐖D10所示。

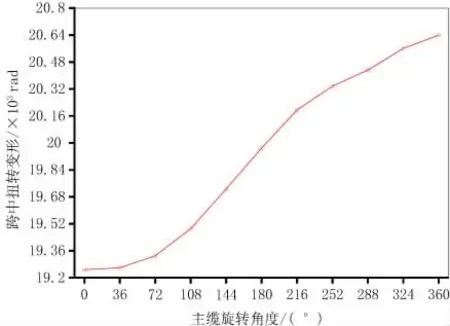
圖10 扭轉(zhuǎn)變形與扭轉(zhuǎn)角度的關(guān)系

從圖中可見，由于主纜的扭轉(zhuǎn)會降低全橋的抗扭剛度，但變化很小。單獨選取任意一根主纜為研究對象，都是純受拉結(jié)構(gòu)，不會有失穩(wěn)的問題。但是如前所述，主纜會產(chǎn)生一個徑向力而積聚了勢能。如果旋轉(zhuǎn)角度小于360°，由于主纜的保向力作用，結(jié)構(gòu)是穩(wěn)定的。但是當主纜的旋轉(zhuǎn)角度大于360°時，會存在所謂的彈性突跳（sn a pt h ro u g h）的風險。也就是結(jié)構(gòu)失穩(wěn)破壞后會在某個節(jié)間形成積聚扭曲，如圖11所示。

圖11 彈性突跳后的結(jié)構(gòu)

彈性突跳一旦發(fā)生，會直接破壞整個結(jié)構(gòu)，實際工程中必須予以避免。單根拉索的旋轉(zhuǎn)角度盡量不要超過360°，這樣可以利用保向力保證結(jié)構(gòu)安全。為了避免彈性突跳的發(fā)生，也可以做成雙層螺旋主纜，如圖12所示。

圖12 雙層主纜三維螺旋主纜懸索橋

5 結(jié) 語

本文構(gòu)思了一種三維螺旋主纜懸索橋方案，并建立了數(shù)值模型驗證結(jié)構(gòu)的可行性。通過對橫向剛度、豎向剛度和扭轉(zhuǎn)剛度的模擬計算，發(fā)現(xiàn)了一些規(guī)律并對其進行了解釋：

（1）三維螺旋主纜懸索橋主纜全部處于受拉狀態(tài)，結(jié)構(gòu)傳力途徑明確，結(jié)構(gòu)可以成立。

（2）三維螺旋主纜懸索橋隨著扭轉(zhuǎn)角度的增加，橫向剛度和豎向剛度都會增加。

（3）三維螺旋主纜懸索橋隨著扭轉(zhuǎn)角度的增加，抗扭剛度變化不大。

（4）主纜扭轉(zhuǎn)形成的桁架管效應是剛度增加的原因。

彈性突跳現(xiàn)象是三維螺旋主纜懸索橋的非線性失穩(wěn)的外在反映，可以破壞整個結(jié)構(gòu)，需要進一步研究。