一種大跨徑“人字形”三角鋼桁架橋的設計與計算

周昱

（廣州市市政工程設計研究總院有限公司，廣東 廣州 510600）

1 工程概況

司馬坡島位于海南省省會海口市中心城區東部的南渡江上，是南渡江河口段的江心島，島的西側是南渡江西岸生活片區的城市主干道濱江路?；陧椖績炘降牡乩砦恢谩u中島的生態和景觀格局，司馬坡島將建成一座包含國際級體育賽事場地、頂級度假設施、多元旅游活動的島中島。司馬坡大橋為連接小島與其西側城市主干路的唯一通道。根據總體布置，橋梁位于一“右進右出”的T字形路口上；考慮到司馬坡島的功能定位，本橋具有很高的景觀性要求，建成后應作為當地的地標性建筑，見圖1。

2 設計簡介

司馬坡大橋為一單跨165m，空間上呈三腳架造型的半穿式鋼桁架橋。上部結構主體為鋼桁梁，主梁外輪廓包裹鈦合金裝飾板，見圖2。橋梁上部結構由兩片高18m，斜向布置三角形桁架構成，其平面呈“人字形”分肢，見圖3。橋設置雙向兩車道及人行道，島嶼側（未分肢側）路面寬10.5m；城市側（分肢側）路面寬7.25m。

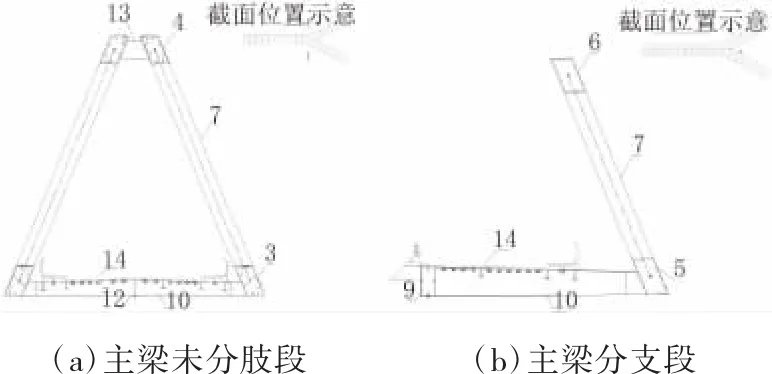
圖3 典型橫斷面

鋼桁主梁由兩種四片內傾的桁架交于一點構成。主梁在空間上整體呈一個等腰三角架造型，桁高最高處即為主梁四片桁架交點。主桁梁兩分肢段夾角為60°，分肢段與未分肢段下弦桿的交角為153°。

立面上桁架采用變高桁架，呈三角形造型。每片桁架節間長度相等為8.88m，均采用N形桁架。橫斷面上，主梁未分肢段兩片桁架一內傾，構成三角形斷面；橋面支撐于橫梁上，橫梁與下弦桿連接。主梁分肢段橫梁半懸臂連接到桁架二上，構成一個”L“形斷面。此段橫梁與主桁架二的豎桿共面，構成一系列大小不一的”L“形鋼架，這些鋼架則通過弦桿和邊縱梁連接起來，共同構成主梁分岔段的兩分肢。鋼桁架主要構件見圖4。

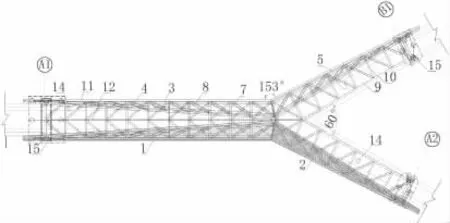
圖4 橋梁主要構件示意

主橋的上、下弦桿采用平弦四邊形截面，與桁架內傾角度一致。豎桿，斜腹桿，邊縱梁構件采用箱型斷面。平縱聯，中縱梁，一般橫梁采用H型斷面（見圖5）。其中弦桿采用Q460qD鋼材，其余構件采用Q420qD鋼材。橋梁采用整體式全焊節點，即每段上、下弦桿即為一預制節點。平縱聯連接中縱梁與下弦桿節點，采用N行布置。橋面采用正交異性板橋面，采用U形加勁肋。

3 靜力計算

圖5 主要構件斷面示意

采用空間桿系模型建立全橋有限元模型，對全橋主要構件進行靜力分析。計算考慮結構恒載（包括一期、二期）、活載（城A、人群荷載及溫度效應）、百年靜風荷載和E2地震荷載。其中風荷載結構風壓由全橋風洞實驗測得；地震荷載采用反應譜分析地震加速度值為0.30g，地震動反應譜特征周期為0.35 s。經計算有以下三個控制工況，工況Ⅰ：標準組合；工況Ⅱ：工況Ⅰ+靜風荷載；工況Ⅵ：恒載+地震力。計算分析模型見圖6。

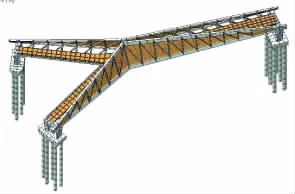
圖6 計算分析模型

3.1 內力結果分析

表1 中給出了主梁各構件的最大內力值，其中弦桿對應圖4中的3～6構件、腹桿對應7～8構件、中縱梁對應12構件、邊縱梁對應9構件、橫梁對應10構件。

由計算結果可以看出上、下弦桿為主要受力構件，軸力為控制內力；同時由于結構呈空間異型結構，弦桿亦承受較大的面內和面外彎矩。由圖 7（a）～（c）可見，主桁構件所產生的拉壓應力分布趨勢是有一致性的。上弦桿和斜腹桿承受壓應力，下弦桿和豎腹桿承受拉應力，這種受力體系是合理的。上弦桿越靠近支座，壓力越大；下弦桿越靠近支座，拉力越大。這是由于立面為三角形桁架，桁高逐漸變小故弦桿軸力相應增大。弦桿的彎矩分布也呈現同樣趨勢，這由于桁架端部為一大節點，剛度較大導致次彎矩集中所致。

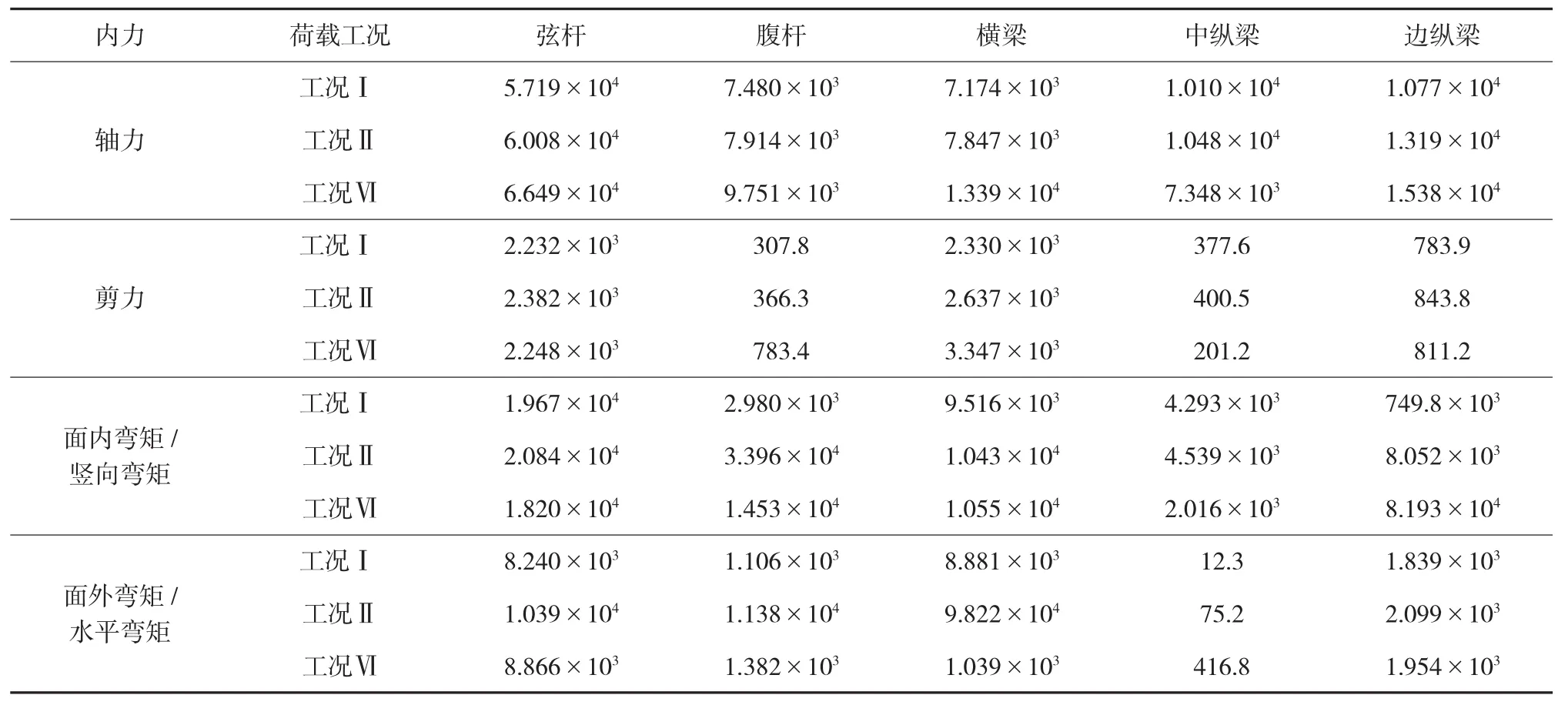
表1 主要構件最大軸力值kN·m

圖7 主要構件內力分布圖（工況Ⅰ）

由表1中結果可以看出，同弦桿一樣，腹桿亦主要承受軸向荷載；同樣值得注意的是腹桿端部承受較大的面內和面外彎矩，且面內彎矩約為面外彎矩的3倍。這是由于桁架采用整體全焊式節點，節點剛度大導致面內次彎矩較大；同時由于桁架為空間結構，其橫向效應致使腹桿承受一定的面外彎矩?；诖耸芰μ攸c，腹桿均設計成箱型截面以增加構件抗彎承載力及面內面外穩定性。

圖 7（d）～（f）給出了橫梁內力分布，位于桁架分肢及支點處的橫梁平衡內傾桁架的水平推力，承受較大的軸向力；其余橫梁均為豎向受彎構件。由圖7（e）可見未分肢側橫梁受力近似于簡支梁，分肢側橫梁受力近似于懸臂梁，這與其主桁架結構特點也是相匹配的。支點處的水平力主要由支點橫梁承擔，故此處承受較大的面外彎矩荷載，故此處橫梁進行加強，采用箱型斷面以提高其水平抗彎能力。

中縱梁及邊縱梁作為板桁橋面體系的一部分，起部分下弦桿的作用；圖 7（g）、（h）中縱梁的軸力分布也印證了這一點，其內力大小分布規律與下弦桿類似。同時由于邊縱梁位于L形分肢端部，亦分擔分肢部分主梁彎矩，其豎向彎矩值明顯大于中縱梁且其內力分布情況亦與其結構構造相匹配；即可看作支撐在邊支座及主梁分肢位置的近似簡支梁。另外由表1可見，由于結構的空間異形特性，邊縱梁還承擔較大的水平彎矩荷載。

3.2 構件應力計算結果

根據上述橋梁受力特點，對不同構件采用相應的截面。橋梁采用容許應力法設計，容許應力值根據板厚折減及受壓構件穩定性進行折減。圖8給出了構件在工況1下的正應力包絡圖，表2給出了主要構件各工況的組合應力值（考慮次應力相應）。可見上弦桿的控制工況為工況Ⅰ，最大壓應力值210 MPa；下弦桿的控制工況為工況Ⅱ，最大拉應力值340 MPa；腹桿、橫梁以及邊、中縱梁的控制工況均為工況Ⅰ，最大組合應力值分別為204MPa、178MPa、209MPa。經驗算構件應力值均小于容許應力，強度滿足規范要求。

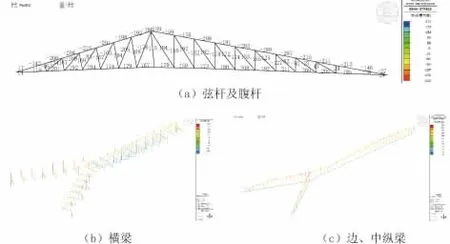
圖8 主要構件應力圖（工況Ⅰ）

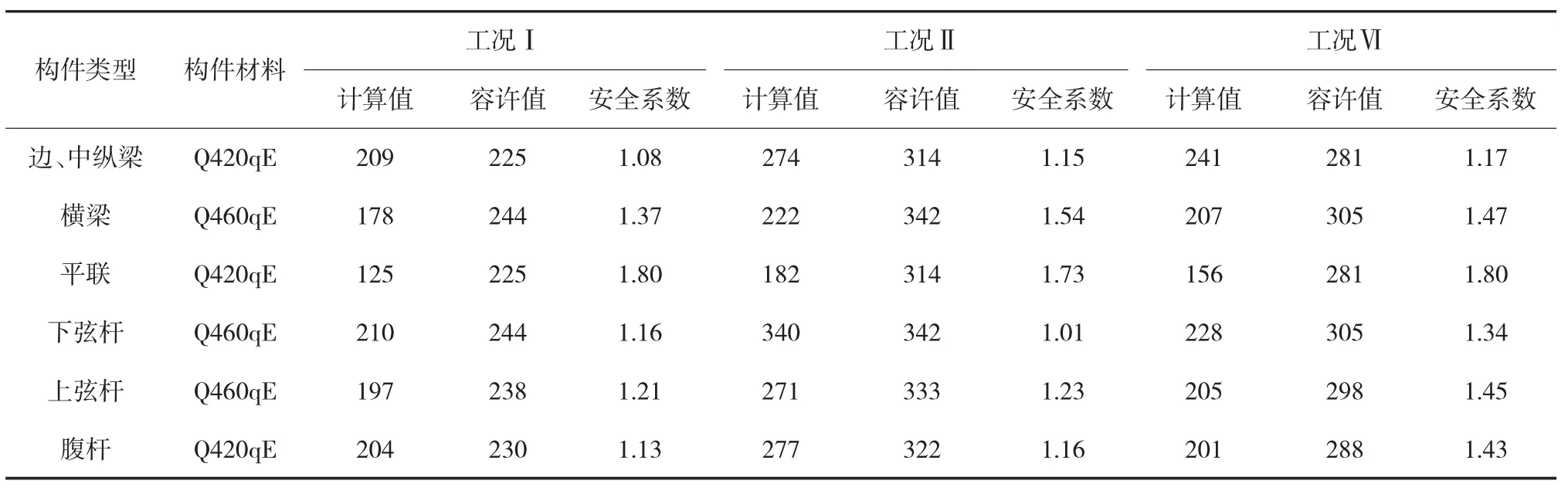
表2 主要構件最大應力值MPa

3.3 位移計算結果

恒載作用下最大撓度發生在上弦桿中部，即由分叉口到小島組成跨的“跨中”位置處。撓度的最大值為495mm。活載作用下最大撓度發生在邊縱梁中部區域，即由分叉口到城市側組成跨的“跨中”位置處。最大活載位移值為75 mm＜L/800=193mm滿足規范要求，見圖9。

圖9 主要構件應力圖（工況Ⅰ）

4 全橋屈曲分析

對全橋進行彈性穩定性分析，分析理論是假設結構在失穩時，處于彈性變形階段，結構內力與外荷載成比例關系，求解過程是把結構的穩定分析轉化為數學上特征值問題。在有限元程序計算中，特征值方程的矩陣形式如下：

式中：[K0]為線彈性剛度矩陣；[Kσ]為參考荷載作用下的幾何剛度矩陣；λ為荷載安全系數。

在有限元計算程序中，求解極限荷載需要進行荷載—位移全過程分析，問題在數學上可歸結為求解非線性平衡方程：

對司馬坡大橋在關鍵工況下的極限承載力進行分析計算，分析方法采用彈性穩定分析。計算中考慮的荷載為：恒載、車輛及人行活載、風荷載。進行屈曲模態分析后，提取前2階屈曲模態見圖10。計算結果可見，第1階失穩模態臨界荷載系數為49.8，失穩模態為上弦桿側向失穩；第2階失穩模態臨界荷載系數為59.6，失穩模態為上弦桿側向失穩+分肢側邊縱梁豎向失穩?？梢娪捎诒緲蛘w呈一類似于三腳架的構造形式，結構穩定系數較高，橋梁穩定性較好。同時前兩階失穩模態都是主桁側彎導致桿件的失穩，即相對豎向剛度，結構的橫向剛度較小。

圖10 前兩階屈曲模態

5 動力特性分析

采用L a nc z o s法對橋梁進行動力特性分析，提取前四階振型見圖11。第一階振型為一階正對稱側彎，頻率0.80 H z；第二階振型振型為一階正對稱豎彎，頻率0.81 H z；第三階振型為一階反對稱豎彎，頻率1.48 H z；第四階振型振型為二階正對稱側彎，頻率 1.71 H z。

圖11 前4階振型

該橋一階振型和二階振型的自振周期較長，體現了大跨度鋼桁架橋整體較柔，結構輕巧這一特性，這對于結構抗震是有利的。另外值得注意的是，第一、二階振型頻率較為接近，即橋梁存在一定的側彎、豎彎耦合的動力特征。

6 結語

隨著我國城市橋梁建設的快速發展，人們對橋梁的景觀造型要求越來越高。鋼橋因為架設速度快，造型美觀多樣，常常會成為城市當中一道亮麗的風景線，在城市橋型中很有競爭力。本文結合司馬坡大橋工程，介紹了一種新式的“人字形”三角鋼桁架橋；并對該橋進行了動、靜力分析計算，得到以下結論：

（1）該橋為空間異性結構，其空間受力效應明顯，桁架桿件承受較大面外力。故多采用箱型截面構件以提高面外/水平抗彎能力。

（2）由于采用了全焊式整體節點，節點剛度大，桁架桿件面內次彎矩大。弦桿彎曲應力（次彎矩及橫向彎矩）約占總設計應力的30%左右，腹桿則達到40%以上。

（3）三角形桁架的主要受力構件為弦桿，上弦桿承受壓力，下弦桿承受拉力。由于橋梁立面為三角形結構，越靠近支座桁高越小，弦桿受力也越大。

（4）該種結構整體穩定性良好，結構較為輕巧抗震性較好；且橋梁造型較為獨特，具備一定的景觀效果，可作為城市景觀橋梁的一種橋型方案。