斜拉橋調索理論及ANSYS實現

張立明，陳 優

（中億豐建設集團股份有限公司，江蘇 蘇州 215131）

0 引 言

隨著設計理論的完善、施工方法的改進和新材料的使用，斜拉橋的發展進入一個嶄新的時代。斜拉橋設計自由度很大，可以通過調整索力來改變結構的受力狀態，一旦斜拉橋結構布置確定，總能找出一組索力，使結構在確定性荷載作用下，某種反映受力性能的指標達到最優。這組索力對應的成橋狀態就是對應指標下的合理成橋狀態，求解這組最優索力，并設法通過施工加以實施，也就實現了斜拉橋的成橋狀態優化。因此斜拉橋承載狀態的優化也就轉化為斜拉橋索力優化問題。

斜拉橋是高次柔性超靜定結構，而且在施工過程中結構體系不斷轉換，如何確定在施工中斜拉索的初張力和體系完成后的二次張拉索力，以達到設計理想狀態并非容易的事情。

斜拉橋的調索方法較多，目前比較常用的主要有剛性支承連續梁法、零位移法、倒拆和正裝法、無應力狀態控制法、內力平衡法等[1]。

ANSYS軟件是融結構、熱、流體、電磁場、聲場和耦合場分析于一體的大型通用有限元分析軟件。作為通用有限元分析軟件，ANSYS軟件為橋梁結構有限元分析提供了新的途徑，可以根據各種理論編制ANSYS程序以更好地滿足橋梁結構分析要求。根據以往的ANSYS使用經驗結合五種調索理論總結出一套切實可行的ANSYS調索手段，可以綜合比較出各種調索理論的優缺點[3]，便于設計者比選出最優設計索力。

1 調索理論及模型計算

本文利用索的實際索力作為控制變量，找出索力的變化規律，建立計算模型，給出各種調索理論的計算數值，進而可以進行綜合比選，選出成橋的最優索力。

什么是最優索力？關鍵是塔直梁平：

（1）塔要直——主塔盡量承受軸向壓力。

（2）梁要平——主梁盡量彎矩比較均勻。

（3）索力均勻——短索索力小，長索索力大。

（4）支座反力——支座不能出現負反力。

為了著重探討調索理論及其方法，對其中許多其他因素進行了忽略。例如，不考慮主塔的變形與受力影響，不考慮主梁的收縮徐變等因素，并且采用塔、梁、墩固結的剛構體系。即以圖1的三索系統為例，來說明斜拉橋的調索理論及ANSYS計算方法。

假設已知鋼索的抗拉剛度為EA1=105kN，主梁的抗拉剛度為EA2=2.1×106kN，抗彎剛度EI為2.1×105kN·m2，均布載荷q0=100 kN/m，并假設三根索受力之前，設計載荷q0已經作用在梁上，即全部主梁架設成功后再開始張拉3根索。

下面以圖2的模型為例，分別介紹各種調索理論及在ANSYS中對模型調索的實現方法。

1.1 剛性支承連續梁法

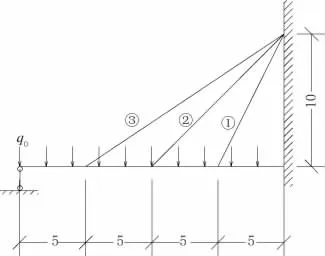
圖1 三索系統示意圖（單位：m）

圖2 ANSYS有限元模型

剛性支承連續梁法是指在成橋狀態下，斜拉橋主梁的彎曲內力和剛性支承連續梁的內力狀態一致，因此可以非常容易地根據連續梁的支承反力確定斜拉索的初張力。

需要說明的是，當主梁具有縱坡時，剛性支承連續梁法的計算結果不能使主梁彎矩真正達到剛性支承連續梁的相應值，而且由于在主塔附近的一段距離內一般不布置斜拉索，按剛性支承連續梁法確定的索力使得靠近主塔的第一對索力很大，而第二對索力很小，甚至出現負值。

ANSYS實現剛性支承連續梁調索的方法如下：

（1）在索梁交點位置建立剛性桿，下端固結，索力置零，按該法求出各個剛性桿的軸力（見圖3）。

圖3 剛性支承連續梁法

（2）根據剛性桿的軸力反算出拉索的軸力，并將剛性桿的剛度置零或直接去掉剛性桿（見圖4）。

圖4 去除剛性支承后迭代索力

（3）將拉索的軸力乘上系數反復迭代直到結構受力和變形趨于合理。

1.2 零位移法

零位移法的出發點是通過索力調整，使成橋狀態下的主梁和斜拉索交點的位移為零。

需要說明的是，以上這兩種方法（剛性支承連續梁法和零位移法）用于確定主跨和邊跨對稱的單塔斜拉橋是最有效的，當主跨和邊跨不對稱時幾乎失去了作用，因為這兩種方法必然導致較大的塔根彎矩，失去了索力優化的意義。

ANSYS實現零位移調索的方法如下：

（1）將索力作為設計變量，各個拉索與主梁的交點的豎向位移為目標函數。

（2）ANSYS將反復迭代設計索力直到豎向位移滿足要求（見圖5）。

證明 設{xn}是關于度量ρ0的Cauchy-列,假設{xn}關于度量d收斂到a,但是0<1。則對任意的ε>0,存在N,使得m,n>N時, ρ0(xn,xm) <ε。不妨設xn> <ε。當m,n→∞時,對任意的ε> 0, a∧(1-a) <ε,得a=0或者a=1。這與0>

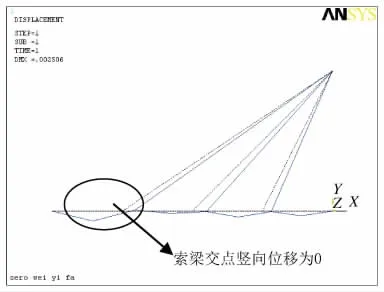
圖5 零位移法

1.3 倒拆和正裝法

倒拆和正裝法是斜拉橋安裝計算廣泛采用的一種方法，通過倒拆、正裝交替計算，確定各施工階段的安裝參數，使結構逐步達到預定的線形和內力狀態。由于斜拉橋幾何非線性和混凝土收縮徐變的影響，倒拆和正裝計算中，兩者會不閉合，即按照倒拆的數據正裝，結構偏離預定成橋狀態的線形和內力狀態，這時需要綜合考慮混凝土收縮徐變的影響。

ANSYS實現倒拆和正裝調索的方法如下：

（1）剛性支承連續梁全橋調平，求出對應的索力。

（2）用單元生死手段實現倒拆和正裝。

（3）此方法的關鍵是，一定要保證正裝殘余索力和倒拆殘余索力相等。

1.4 無應力狀態控制法

無應力狀態控制法分析的基本思路是：不計斜拉索的非線性和混凝土收縮徐變的影響，采用完全線性理論對斜拉橋解體，只要保證單元長度和曲率不變，則無論按照何種程序恢復還原后的結構內力線形將與原結構一致。應用這一原理，建立斜拉橋施工階段和成橋狀態的聯系。

考慮結構在荷載作用下變形后斜拉索兩端節點的幾何長度扣除斜拉索單元軸力產生的伸長量后即是斜拉索的無應力索長[4]。

則該例子中的無應力索長即為不受力狀態下兩個錨固點間的距離：

現將拉索均按照理想成橋狀況的索力進行張拉（此索力為其余調索方法求出的索力平均值），張拉后各個拉索均有了初始內力。

算出各個拉索的伸長長度，并算出各個拉索的豎向變位值，見表1。

根據豎向位移h算出實際索長L（見圖6）：

式中：L0為無應力索長；h為錨固點豎向變形；L為拉索實際長度；α為拉索與豎向位移的夾角。

通過計算可求得各個錨固點的豎向變形（見圖7），可明顯看到各個錨固點的變形均小于1.5mm，根據變形差求出需要增加的索力。

ANSYS實現無應力狀態控制調索的方法如下：反復迭代索力值直到拉索的兩個錨固點之間的距離為無應力索長（見圖7）。

在初始索力作用下，各個拉索節點均有一定的變形，此時各個拉索錨固點變形均小于1.5mm。

根據拉索伸長量對拉索索力進行微調，調整后各個拉索的索力計算結果見表1。經迭代計算拉索伸長量可控制在0.1mm以下，索力增加值可精確到0.1 kN，工程精度一般控制在2%以下，故調索索力滿足設計要求。囿于篇幅本文只摘抄初始張拉、第一次和第五次調索結果，如圖8、圖9所示。

表1 無應力狀態法調索結果

圖6 索長計算圖

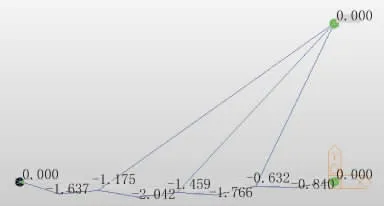
圖7 初始索力作用下各個節點的變形（單位：mm）

第一次調索時，各個拉索錨固點變形均小于1 mm。

第五次調索時，各個拉索錨固點變形均小于0.1mm。

1.5 內力平衡法

內力平衡法的基本原理是設計適當或合理的斜拉索初始張力，以使結構各控制截面在恒載和活載共同作用下，上翼緣的最大應力和材料允許應力之比等于下翼緣的最大應力和材料允許應力之比。

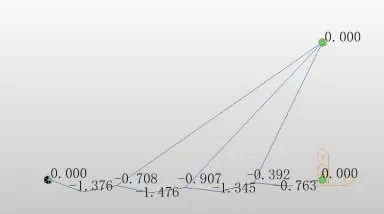
圖8 第一次調索力作用下各個節點的變形（單位：mm）

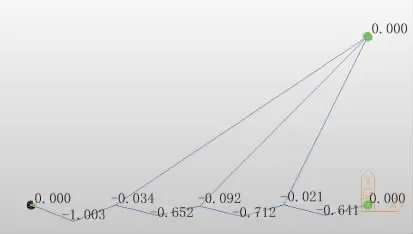
圖9 第五次調索力作用下各個節點的變形（單位：mm）

ANSYS實現內力平衡調索的方法如下：

將單元抗彎剛度取為實際值的1/1 000，施加結構自重等外載荷，做一次落架線性計算，所得索力就是彎曲能量最小時候的最優索力，局部調整單元抗彎剛度、支承剛度和拉索抗壓剛度，進一步優化結構內力，可將其作為斜拉橋成橋合理狀態[2]，彎矩如圖10所示。

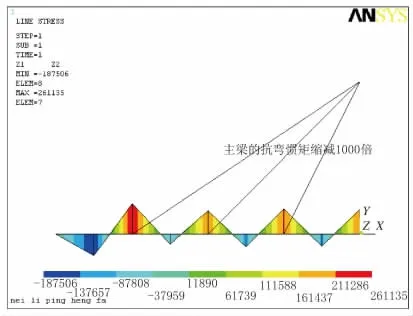
圖10 內力平衡法彎矩圖（單位：N·m）

2 結 語

以上文各種調索理論對舉例模型進行調索計算，各種方法下各個主梁單元的內力以及拉索索力匯總見表2、表3。

表2 不同調索方法計算的主梁內力匯總 kN·m

表3 不同調索方法計算的索力匯總 kN

基于現有調索方法，ANSYS可以用不同的手段實現全橋調索。對于常規桿系結構來說，上述五種方法均能實現全橋調平，但是結合具體橋梁資料，可以選擇一種最優的調索結果使得全橋的內力和變形相對最優。