大型風力發電機塔筒屈曲分析
盧念
采埃孚(天津)風電有限公司 天津 300402
1 塔筒壓桿穩定性理論分析
1.1 模型描述
根據塔筒實際模型,我們先假定塔筒為一細長桿,可以用下式來描述不同約束條件下細長壓桿的臨界力[1-2]:

其中,截面慣性矩I應取其最小值Imin;E為材料彈性模量;μ為長度因數,它反映了桿端約束條件對臨界力的影響,本模型為一端固定,一端自由,取μ=2; 為桿長度,即計算塔筒高度。
1.2 計算過程
(1)截面慣性矩I的計算:
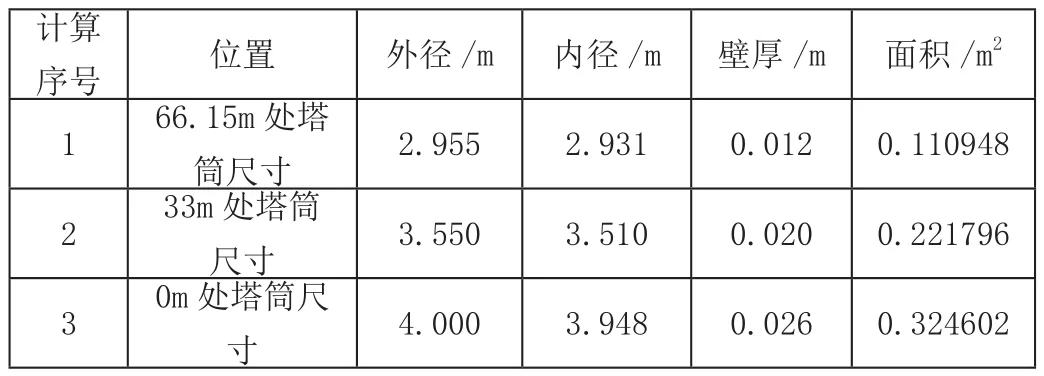
表1 塔筒截面慣性矩計算數據
塔筒為圓環形,截面慣性矩計算公式[3]:

計算結果為:
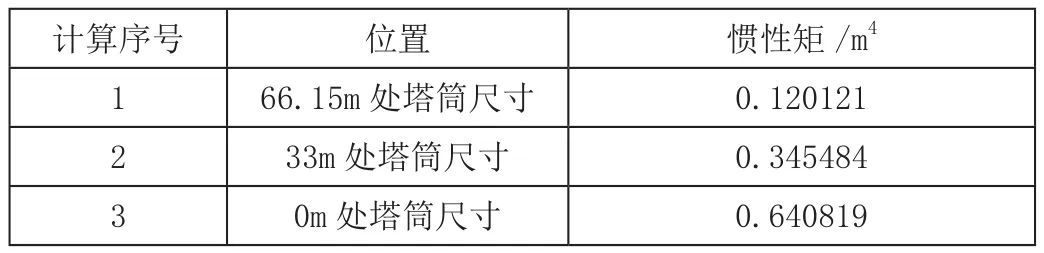
表2 塔筒截面慣性矩計算結果
(2)臨界壓力Fcr的計算:
運用公式(1)可直接得到塔筒的臨界壓力,結果如下:
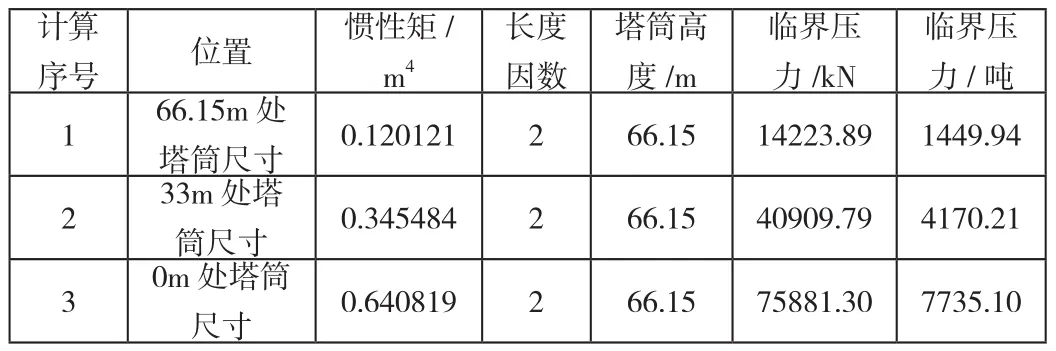
表3 塔筒臨界壓力計算
(3)慣性半徑的計算:

其中I為慣性矩,A為截面積,得到塔筒的慣性半徑如表4所示:
2 塔筒屈曲有限元分析
2.1 模型描述
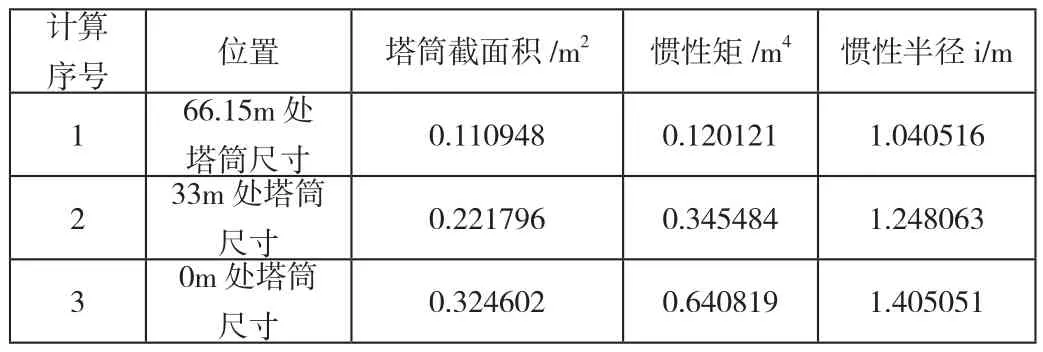
表4 塔筒截面慣性半徑計算
整體靜強度分析采用的模型為:塔筒筒體按圖紙尺寸建模并考慮焊縫。塔筒筒體頂端截面中心處加一個無質量點,坐標為(0,0,66.15),用無質量梁連接到塔筒頂端外圈節點上,筒體上對門框和門洞進行建模,門框和塔筒壁的關系為粘接(GLUE)關系,模型網格均為六面體網格,沿塔筒壁厚方向劃分兩層單元,總單元數為28851個,總節點數為157151個。整體模型如圖1所示。
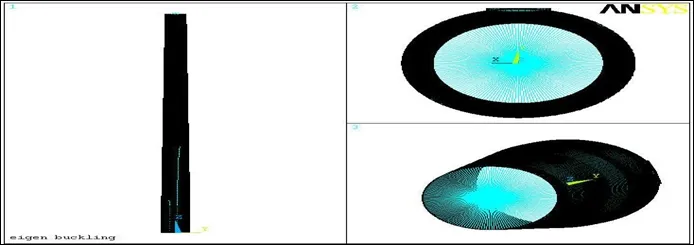
圖1 屈曲分析模型
模型采用的單元形式和材料常數設置如表5:
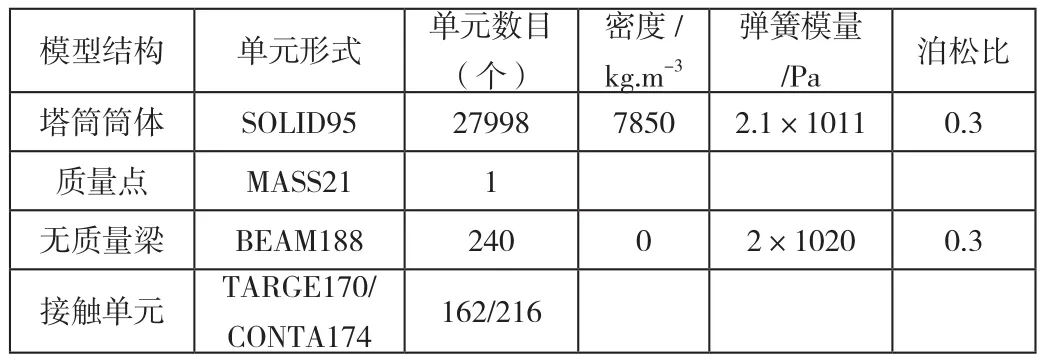
表5 塔筒屈曲計算模型中使用的單元形式和材料常數
2.2 加載方式
對塔筒頂端截面中心無質量點加載:Fz=-1N。
2.3 邊界條件
塔筒底面全約束。
2.4 模型簡化說明
模型中未考慮法蘭、螺栓及其質量。
2.5 模型中使用的坐標系
計算中采用X-Y-Z右手坐標系的笛卡兒坐標。
2.6 屈曲計算結果
有限元軟件輸出的結果如下:
**** INDEX OF DATA SETS ON RESULTS FILE *****
SET TIME/FREQ LOAD STEP SUBSTEP CUMULATIVE
1 0.30585E+08 1 1 1
所加載荷是單位載荷,所以計算得到的一階屈曲特征值就是屈曲臨界載荷,即Fcr=30585kN,可以看出有限元計算的結果在理論計算的范圍內,說明計算結果是可信的。
總之,屈曲荷載屬于完善結構的分叉失穩荷載,實際結構由于缺陷的影響失穩模式通常是極值點失穩,其極限荷載較屈曲荷載明顯降低。為了得到更接近實際的失穩荷載,應對結構進行考慮結構非、材料塑性以及初始缺陷影響的屈曲分析。針對筒殼結構對缺陷敏感的特性,本文采用考慮結構初始缺陷的屈曲分析方法,將屈曲分析得到的屈曲模態按實際的缺陷大小限值歸一化后作為塔筒結構的初始缺陷,并采用弧長法求解塔筒結構的荷載位移曲線,從而獲得實際結構屈曲時的臨界荷載。

