基于核的k-最近鄰在水下目標識別中的應用?
嚴良濤 項曉麗
(1 中國人民解放軍91388部隊 湛江 524022)
(2 廣州杰賽科技股份有限公司 廣州 510220)
0 引言
水下輻射聲場和水聲信道的復雜性是造成水下目標識別難度大的根本原因[1]。這兩方面因素的影響使聲吶接收的噪聲信號都是相互耦合、調制甚至畸變的,因此研究者們提出了多種特征提取方法[2?4],試圖從不同角度得到噪聲信號的特征,但水下環境的復雜性決定了這些特征必然呈現強非線性[5]。在目標識別過程中,為保證識別的正確率應將多種特征加以組合,但這會造成數據維數過高,識別速率下降。為此,本文提出了基于核(Kernel)的k近鄰[6](k-nearest neighbor,k-NN)水下目標識別方法。該方法利用主成分分析[7](Principal components analysis,PCA)對高維的特征矩陣進行降維,解決目標識別速率低的問題;利用Kernel技巧將降維后的非線性特征映射到高維空間并在該空間進行k-NN分類識別,能夠有效減小非線性特征在低維度空間距離度量誤差,提高識別正確率。實際實驗數據的驗證結果表明:與k-NN相比,基于核的k-NN的目標識別速率略低,但目標的識別正確率得到較大提高;與BP神經網絡分類器相比,基于核的k-NN的目標識別正確率略低,但目標的識別速率得到較大提高。
1 基于核的k-NN基本原理
1.1 空間映射及核函數
給定特征樣本x,將其從n維特征空間映射到m維特征空間:

其中,S1為原始n維特征空間,S2為m維映射特征空間。x為S1中的特征樣本,ψ(x)為對應S2中的特征樣本。ψ為將S1映射到S2的非線性映射,φi為特征映射函數,i=1,···,m。
對x,y∈S1,其核函數(Kernel)表示形式為
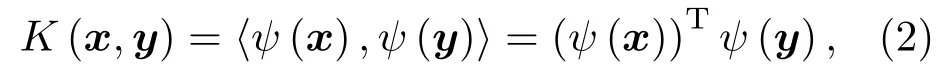
1.2 k-NN的核化
在k-NN中,原始空間特征樣本x和y之間的距離二范數為
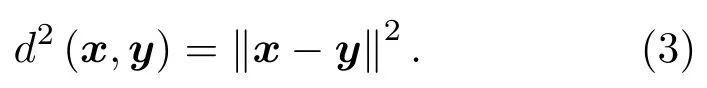
假定將x和y映射至高維特征空間中,那么此時高維空間特征樣本ψ(x)和ψ(y)之間的距離二范數為
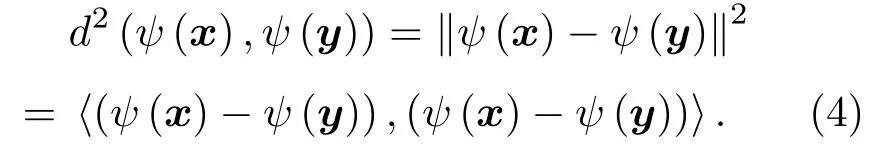
式(4)中存在內積項?(ψ(x)?ψ(y)),(ψ(x)?ψ(y))?,根據1.1節可知,利用Kernel可實現對該內積的直接計算。此時:
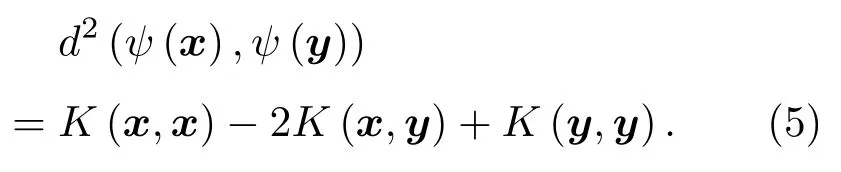
由式(5)可知,高維特征空間樣本ψ(x)和ψ(y)之間的距離可通過Kernel在原始空間中直接計算,而不受維度和映射ψ的限制。
1.3 基于核的k-NN的算法實現
基于核的k-NN的實現過程如下:給定一個用于訓練的特征數據集,將其映射到高維特征空間,對新的輸入實例,利用Kernel計算其在高維特征空間中最鄰近的k個實例,若這k個實例的大多數屬于某個類,就把該新實例劃分為這個類。本文選擇高斯核函數進行運算,具體過程如表1所示。

表1 基于核的k-NN的算法實現過程Table 1 The algorithm of k-NN based on Kernel
在上述實現過程中選擇的高斯核函數靈活度高,不同的核參數C可以將原始空間映射到任意維空間。在對核參數C的優化過程中,C值過大,高次特征上的權重衰減快,所映射出空間相當于原始空間的子空間;C值過小,可將任意數據映射至線性可分的空間,但這很可能帶來嚴重的過擬合問題[8],因此C值的優化尤其重要。k值的確定采用在一定范圍內[9](樣本量開平方附近)進行枚舉計算確定。
2 基于核的k-NN在水下目標識別中的應用
2.1 數據來源與預處理
將實測的166段水下目標噪聲信號進行篩選、標記和梅爾頻率倒譜系數(Mel frequency cepstrum coefficient,MFCC)特征提取[10]后,得到120組特征數據,分屬4類目標,每類30組,將其中20×4組作為訓練樣本集D(22×80),其余10×4組作為測試樣本集T(22×40)。利用PCA對訓練樣本集D進行降維,具體過程如表2所示。

表2 PCA的降維過程Table 2 The algorithm of reducing dimensionality with PCA
這樣就可以將一個特征樣本x映射到一個d′維特征子空間上去,此空間的維度小于原始的d維空間:
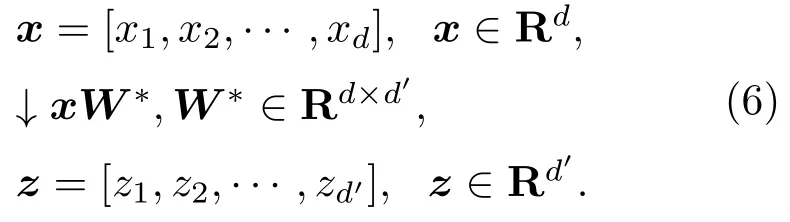
本文取閾值t=95%,根據計算確定d′=16,其方差貢獻圖如圖1所示。
從圖1可看出,第一主元占方差總和的22%左右,前16個主元占總體方差的95%左右。
訓練樣本集D(22×80)經過PCA降維后就轉換成低維數據集Z(16×80),接下來就可以在矩陣Z中利用1.3節中的基于核的k-NN進行分類。
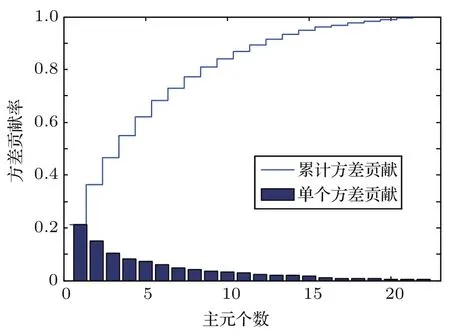
圖1 PCA方差貢獻圖Fig.1 Variance contribution graph with PCA
2.2 訓練過程及分析
選擇高斯Kernel進行距離度量計算,不同核參數C值代表將數據集Z(16×80)={z1,z2,···,z80}映射到不同的高維空間。在最優C值的高維空間內同一類別的樣本最聚集,正確分類識別率最高。核參數C值的優化屬于超參數優化問題[11],本文采用sklearn.grid_search模塊下的GridSearchCV對象對C值進行優化,其主要應用對象為小數據集,基本原理是對人工設置的超參數進行網格搜索得到最優值;若算法中存在多個超參數需優化,那么依次選取對模型影響最大的參數調優,直到所有的參數調整完畢。本文中只涉及核參數C值的優化,應用上述方法得到的最優值為45.62。
對k值在樣本量開平方附近進行枚舉計算確定,得到在訓練樣本中不同k值與識別正確率之間的關系如圖2所示。
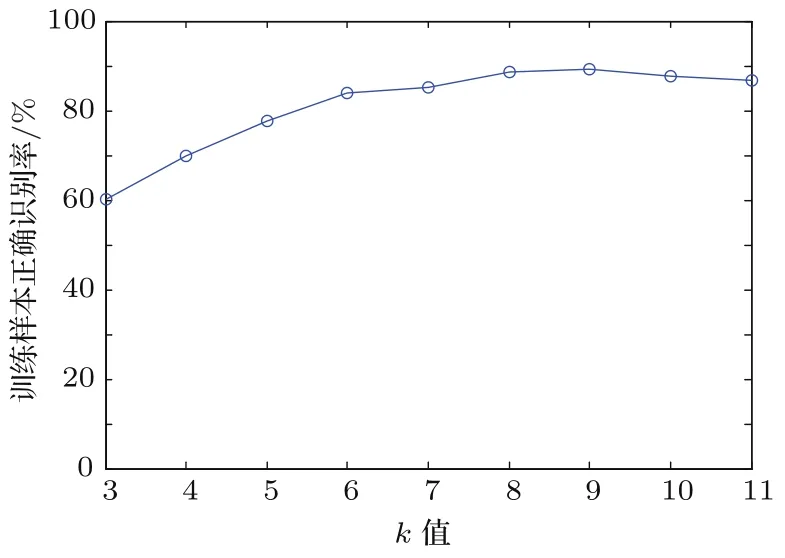
圖2 k值與識別正確率之間的關系Fig.2 The relationship between k and recognition accuracy
從圖2可看出,k=8時識別正確率最高約為88%,實際值為88.23%。
2.3 驗證與比較
根據2.1節和2.2節得到的最優d′、C及k值,將測試樣本T(22×40)進行分類并與各樣本類別標簽進行對比得出識別正確率,同時計算每個測試樣本識別過程的消耗時間t。與傳統線性k-NN和BP神經網絡分類器的比較如表3所示。
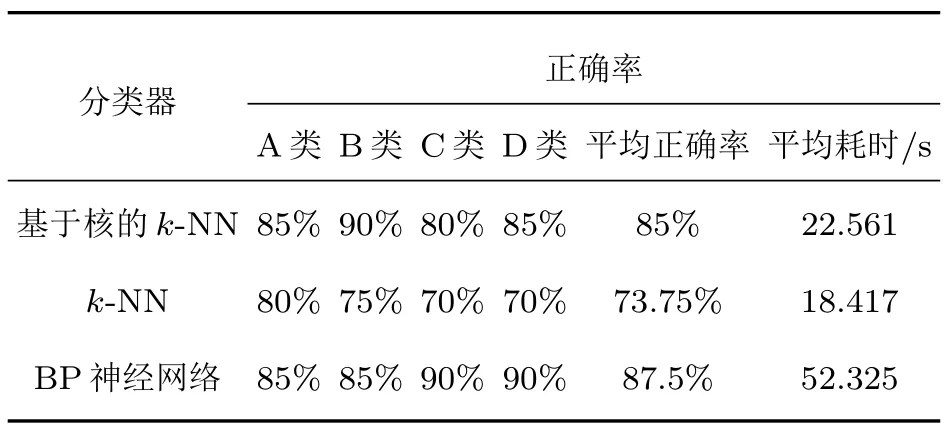
表3 基于核的k-NN、k-NN和BP神經網絡分類器性能比較Table 3 The performance comparison of k-NN based on Kernel,k-NN and BP neural network
由表3可知,基于核的k-NN分類器的平均識別正確率為85%,高于k-NN分類器11.25%,低于BP神經網絡分類器2.5%;平均耗時為22.562 s,高于k-NN分類器4.144 s,低于BP神經網絡分類器33.908 s。BP神經網絡分類器平均識別正確率雖略高于本文基于核的k-NN分類器,但其平均耗時超出基于核的k-NN分類器一倍多;k-NN分類器的平均耗時略小于基于核的k-NN分類器,在可接受范圍內,但其平均識別正確率相對于基于核的k-NN分類器過低。所以得出結論:相對于k-NN分類器和BP神經網絡分類器,基于核的k-NN分類器綜合性能更優。
3 結論
本文利用Kernel技巧將原始空間數據映射至高維特征空間,實現了原始空間的非線性耦合數據在高維特征空間的線性可分,有效解決了水下目標特征數據非線性不可分的問題。并采用PCA對特征數據矩陣進行降維,利用k-NN進行分類識別,形成了基于核的k-NN水下目標識別方法。通過與傳統k-NN和BP神經網絡分類器對比,說明了基于核的k-NN分類器性能的優越性。

