水下機械手分數階積分滑模軌跡跟蹤控制方法研究
黃道敏 韓麗君 唐國元 周曾成 徐國華
1.華中科技大學船舶與海洋工程學院,武漢,4300742.空軍預警學院預警技術系,武漢,430010
0 引言
海洋研究領域的逐步擴展,對水下自主航行器(autonomous underwater vehicle, AUV)的續航及作業能力提出了更高要求,這往往需要利用水下固定或移動平臺對AUV進行捕獲和對接,從而進行能源補充及數據交互。在固定或移動平臺上安裝水下機械手來實現對運動狀態下AUV的捕獲及對接作業是其中的重要方式之一。
考慮機械臂搭載于固定式平臺捕捉水下航行器的情況,可將該系統的水下捕獲對接過程簡化為具有固定基座的水下機械手末端執行器對航行器的軌跡跟蹤問題。目前提出的控制方法很多,包括PID控制[1]、自適應控制[2]、滑模控制(SMC)[3]、反演控制[4]、模糊理論[5]和神經網絡控制[6]等,還包括采用以上兩種及兩種以上的混合控制技術。其中,滑模控制因具有操作簡單、響應速度快、對系統的不確定性不敏感等特點而被廣泛采用。滑模面的選擇和控制律的設計是決定滑模控制性能的兩個關鍵因素。文獻[7-9]采用了線性類型的滑模面,如PID型滑模面,其中文獻 [7]對趨近律函數進行了改進。文獻[10-11]采用了非線性類型的滑模面,如終端滑模面,且文獻[10]設計了一種新的分層終端滑模面。由于線性滑模面是關于誤差及其導數或積分項的線性函數,因此只能實現漸近收斂。有些終端滑模控制方法雖然能夠保證在有限時間內收斂,但是仍然需要考慮存在的奇異性問題,文獻[12-13] 通過修改終端滑動面來解決奇異性問題。
本文采用分數階理論,設計了一種基于指數趨近律的分數階積分滑模控制方法,避免了奇異性問題。由李雅普諾夫理論的分析可知,該控制方法可以保證系統的漸近穩定性。通過對六自由度水下機械手對運動目標的軌跡跟蹤控制的數值仿真,驗證了所提控制方法的有效性和魯棒性。
1 機械手的動力學模型
1.1 問題描述
機械手對運動目標的軌跡跟蹤見圖1。背部安裝有導桿的航行器在確定的XY平面自主航行,其航行路線處于機械手末端執行器的工作空間范圍內時,機械手控制系統可以通過傳感器(如雙目視覺)獲得目標導桿的精確位置和姿態信息,并將其作為此時機械手末端執行器的目標信息。控制系統將機械手實際的位置和姿態信息與目標信息進行比較,并將兩者的誤差在控制器中進行計算, 然后輸出相應的關節控制力矩來實時調整機械臂的各個關節角度。經過一段時間,機械手末端執行手爪最終能夠捕獲安裝在航行器上的目標導桿。
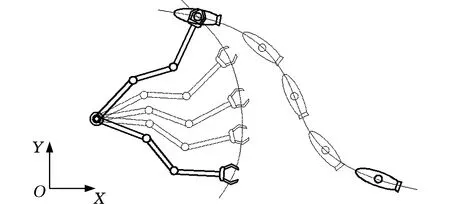
圖1 機械手對運動目標的軌跡跟蹤示意圖Fig.1 The diagram for a manipulator to track a moving target
1.2 動力學方程
本文所采用的六自由度水下機械手構型見圖2。使用D-H方法描述該結構[14],為每一個連桿分別定義4個量,包括連桿扭角αi-1、連桿長度ai-1、兩連桿距離di、兩連桿夾角θi(i=1,2,…,6)。所建立的機械手坐標系見圖3,相應的連桿參數見表1。

圖2 機械手構型Fig.2 The configuration of the manipulator

圖3 連桿坐標系Fig.3 The frame of the manipulator表1 六自由度機械手連桿參數Tab.1 The link parameters of the 6DOF manipulator
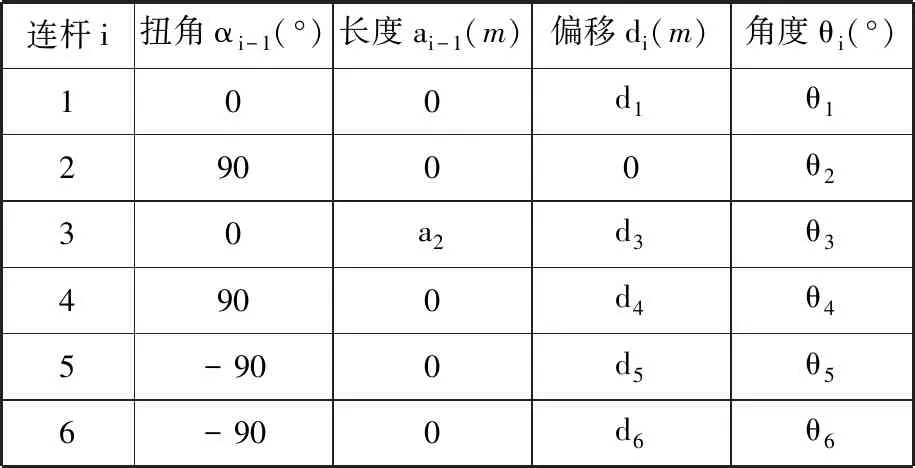
連桿i扭角αi-1(°)長度ai-1(m)偏移di(m)角度θi(°)100d1θ129000θ230a2d3θ34900d4θ45-900d5θ56-900d6θ6
六自由度水下機械手的動力學方程表示為
(1)

式(1)具有如下特性:
M(q)=(M(q))Τ
|M(q)|>0
為了簡化式(1),定義

則由式(1)可得
(2)
這里將未知的外部擾動看作模型的不確定性,忽略摩擦力等因素的影響。
2 分數階積分滑模控制
圖4所示為水下機械手對航行器軌跡跟蹤控制的框架。系統利用傳感器得到每個采樣時刻目標觀測點的位姿信息,并對該信息進行處理,以獲得各個時刻的包含六自由度位置和姿態的齊次變換矩陣,經過逆運動學求解,得到相應的機械手末端的期望關節軌跡,在經過觀察和反饋、并與實際的關節軌跡進行比較后獲得系統的跟蹤誤差。采用分數階積分滑模面來設計控制器的輸入,其輸出結果作用于控制對象以形成完整的閉環系統。
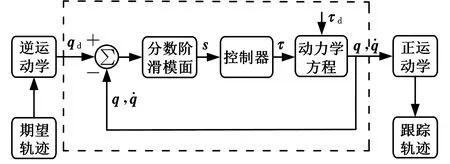
圖4 軌跡跟蹤控制過程Fig.4 The trajectory tracking control process
2.1 控制器設計
令qd為給定的二階可微的期望關節矢量,定義跟蹤誤差e=qd-q,e=(e1,e2,…,e6)Τ。設計分數階積分滑模面:

(3)
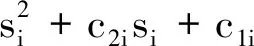
(4)
0<α2i<1i=1,2,…,6

在滑動階段,si(t)=0(i=1,2,…,6), 即

(5)
并且它的導數為
(6)
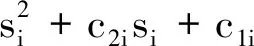
設計控制輸入:
(7)
s=[s1s2…s6]Τc1=diag(c11,c12,…,c16)
c2=diag(c21,c22,…,c26)
(sign(ei)|ei|α1i)i=
[sign(e1)|ei|α11… sign(e6)|e6|α16]T


對s關于時間求導數,結合式(3)和式(7),可得
(8)
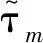
2.2 穩定性分析
考慮一個正定李雅普諾夫函數
(9)
對(9)關于時間求導數,并且利用式(8)得到:

(10)
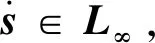
3 仿真
機械手連桿參數a2=5 m,d1=1.195 m,d3=0.7 m,d4=6.4 m,d5=-0.7 m,d6=-0.995 m,連桿密度為2 700 kg/m3。假設水下機械手的重力和浮力的中心是一致的,重力加速度為9.8 m/s2,水密度為1 025.9 kg/m3,流速為(0.5,0.5,0)m/s;水阻力系數Cd=0.6;附加質量力系數Cm=1。式(3)中的滑模面參數設為:c11=100,c12=120,c13=120,c14=100,c15=100,c16=100,c21=50,c22=60,c23=60,c24=50,c25=50,c26=50,α2i=0.9,i=1,2,…,6。目標航行器的動力學方程參數取值參考文獻[16-17],如表2所示。考慮航行器在基坐標系下的z=0.5 m平面上運動。整個系統是基于計算機數值模擬進行的,以檢驗所提出控制律的有效性。
趨近律參數ε=0.5、ki=30,外部干擾τd為分量在[-100,100]N·m范圍的隨機分布向量,仿真結果見圖5。圖5所示為機械手末端的跟蹤軌跡和航行器的運動軌跡,可以看出在t=0時二者的初始位置的距離較遠,隨著時間的推移,最終使得它們的位置相差很小。二者在X方向、Y方向上的位置誤差如圖6、圖7所示,可以看出這兩個位置誤差約在t=2.5 s、t=1 s時首次達到誤差零點,并且在后面的時間里分別實現約為[-0.02,0.02]m、[-0.01,0.01]m的穩態誤差響應。由于控制器的不連續性以及外部干擾的影響,使得在X方向、Y方向上的位置誤差都會產生一定程度的抖振現象,這從局部放大圖中可以看出。

表2 目標航行器動力學方程參數Tab.2 The parameters of the dynamics equation for the target vehicle

1.目標軌跡 2.機械手跟蹤軌跡圖5 存在干擾 [-100,100]N·m條件下的運動軌跡Fig.5 The trajectory with disturbance [-100,100] N·m
趨近律參數ε=0.5、ki=30,無外部干擾時的仿真結果如圖8、圖9所示。在X方向、Y方向上的位置誤差僅在不連續性的影響下產生較小的抖振。

圖6 存在干擾 [-100,100]N·m條件下的X方向的位置跟蹤誤差Fig.6 The tracking error in X direction with disturbances [-100,100]N·m

圖7 存在干擾 [-100,100]N·m條件下的Y方向的位置跟蹤誤差Fig.7 The tracking error in Y direction with disturbance [-100,100]N·m
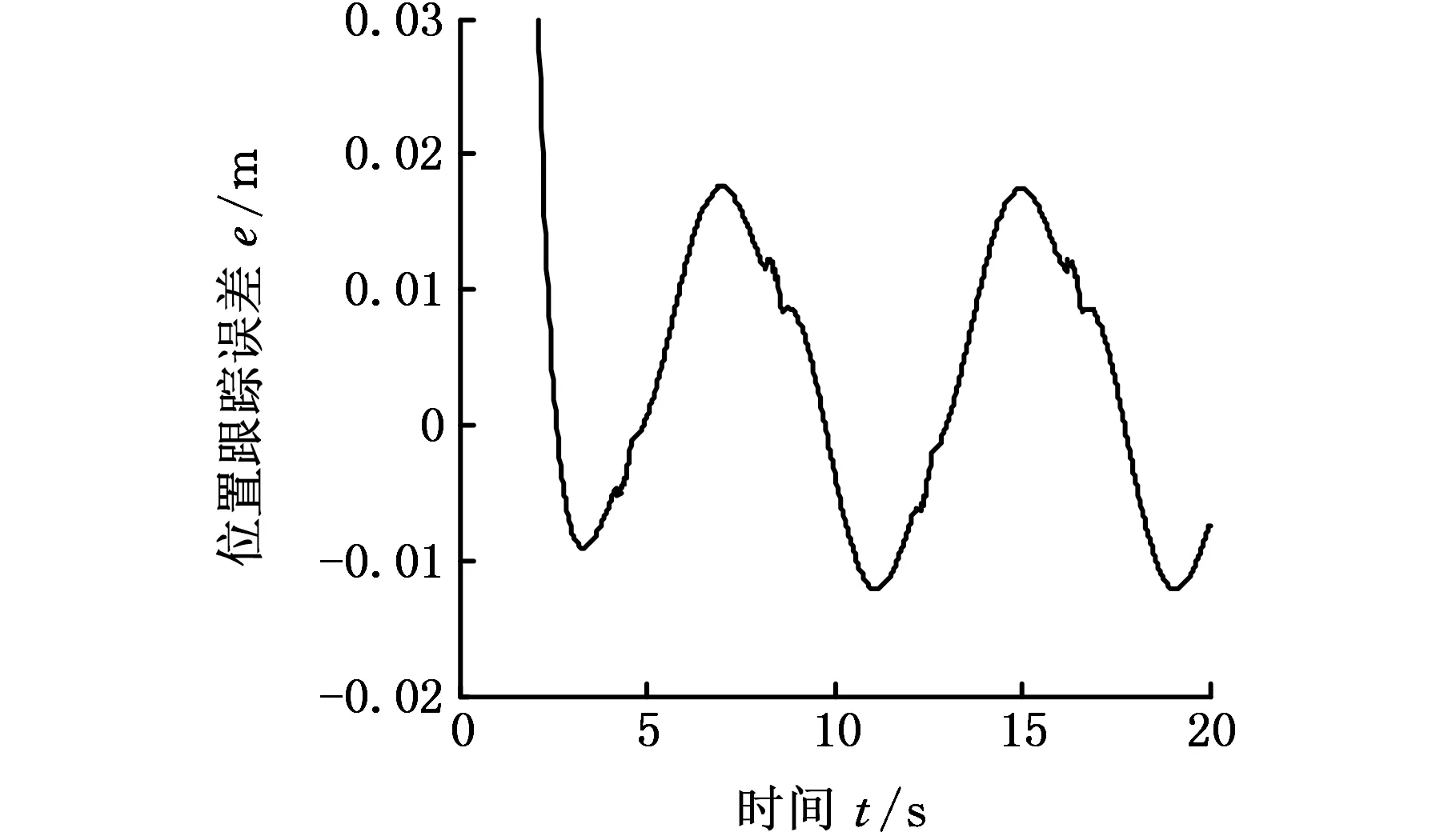
圖8 無干擾條件下的X方向的位置跟蹤誤差Fig.8 The tracking error in X direction without disturbances

圖9 無干擾條件下的Y方向的位置跟蹤誤差Fig.9 The tracking error in Y direction without disturbances
趨近律參數ε=0.5、ki=30,外部干擾τd為[-50,50]N·m的隨機分布向量,此時的仿真結果如圖10、圖11所示。


圖10 存在干擾[-50,50]N·m條件下的 X方向的位置跟蹤誤差Fig.10 The tracking error in X direction with disturbance [-50,50]N·m

圖11 存在干擾 [-50,50]N·m條件下的 Y方向的位置跟蹤誤差Fig.11 The tracking error in Y direction with disturbance [-50,50]N·m
4 結論
本文提出了一種分數階積分滑模控制方法,對于未知外部擾動下的水下機械手的軌跡跟蹤問題,在模型中添加了外部擾動的近似估計項,使得系統可以實現快速收斂,而且還具有較強的抗干擾能力。對六自由度水下機械手的跟蹤問題進行了仿真,結果表明,該控制系統不僅能夠實現高精度的軌跡跟蹤性能,而且還具有較強的抗干擾能力,從而驗證了該控制器的有效性。

