新零售模式下零售商服務水平對雙渠道定價策略的影響分析

王曉梅，林 萍，鞏永華 WANG Xiaomei,LIN Ping,GONG Yonghua

（南京郵電大學 管理學院，江蘇 南京 210009）(School of Management,Nanjing University of Posts and Telecommunications,Nanjing 210009,China)

0 引言

互聯網時代以來，電子商務的發展一直沖擊著傳統零售業，使實體零售商的市場份額急劇縮減。根據CNNIC發布的數據[1]，截止2018年12月31日，我國網民規模已經達到8.29億，網絡購物的用戶規模已達到6.1億人，零售商紛紛調整產業配比，實體零售開辟網絡渠道，傳統實體的客戶也可以享受網絡購物，利潤增速逐漸回升；網絡電商的客戶逐漸趨于飽和，各電商平臺開始了線下整合。例如，阿里零售通事業部2018年8月28宣布，將利用阿里的大數據優勢，幫助全國建成600萬家零售店，京東也致力于線下融合，一年內開設92家實體店，并計劃2018年將門店數量提升至15 000家。實體和網商的相互沖擊下，零售行業經歷前所未有的改革重塑，代表雙渠道新融合趨勢的新零售成為未來零售業發展重心。

由于庫存、運輸、店面等成本的差異，導致雙渠道的服務水平、價格的差異性和交叉影響。而現在的消費者越來越注重消費體驗，服務水平對顧客購物行為的影響逐漸升高[2]，如何在考慮服務水平的基礎上進行渠道定價決策，成為各大雙渠道零售商需要重點關注和解決的問題。

雙渠道供應鏈定價問題從2010年開始成為研究熱點，積累了豐富的研究成果，其研究熱點主要集中于3個方面：雙渠道合作背景下，制造商和零售商的相互關系[3-4]；閉環供應鏈背景下的雙渠道定價問題[5-6]；雙渠道定價的影響因素分析[7-8]。服務水平是雙渠道供應鏈定價決策的重要影響因素，近年來越來越受學者關注，主要聚焦于3個方面：服務溢出效應的影響[9-10]；服務合作[11-12]；服務異質性[13]。現有研究對新零售背景下由單一零售商控制的雙渠道服務研究幾乎空白，僅有劉曉峰[14]針對零售商建立的雙渠道，考慮消費者的線上線下渠道轉換的定價策略差異。本文擬建立單一零售商控制的雙渠道銷售模型，將雙渠道提供的服務水平作為變量，采用價格需求模型，求解雙渠道最優定價、需求與利潤的均衡解，同時將服務溢出效應作為函數參數，探討雙渠道的不同服務水平對最優定價策略和需求的影響。

1 模型構建

1.1 問題描述與假設

本文建立單一零售商控制的雙渠道銷售模型，兩個渠道銷售同種產品、提供差異化服務。由于網絡渠道和傳統渠道可能分屬于零售商不同的利潤部門，協同競爭思維下，其運營管理存在單獨決策或者是總部統一決策的情形，因此，本模型考慮零售商分別采用集中定價策略和分散差異化的定價策略時，服務水平變化對定價決策的影響。

本文模型建立在以下假設的基礎上：

（1）雙渠道零售商的決策理性，接受風險程度中性，完全信息市場。

（2）ki〉ei〉0,i=1,2表示價格變動對渠道的需求影響大于渠道間價格水平差異變化的影響，服務水平變動對需求的影響大于渠道間服務水平差變化的影響。

（3）簡化研究起見，本文不考慮市場中其他零售商的價格競爭帶來的定價影響；假設需求只受渠道價格和服務水平的影響。

（4）文中所有參數都為正。

如圖1結構，零售商在傳統渠道以價格p1向消費者銷售某產品，同時在傳統渠道提供服務水平為s1的服務；同樣的，在網絡渠道以價格p2和服務s2向消費者銷售。消費者以其對服務與價格的不同敏感度分為三類市場。

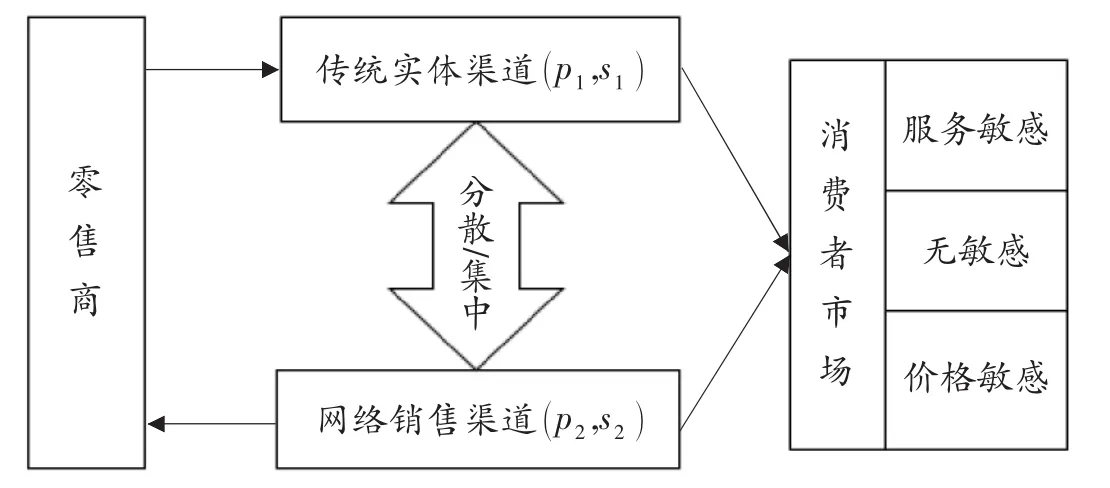
圖1 雙渠道零售商銷售模式

參數和變量進行說明：

D——渠道需求，D1,D2分別表示傳統實體渠道和網絡銷售渠道。

π——零售商總收益，π1,π2分別表示實體和網絡渠道的收益。

p——決策變量，p1表示傳統渠道銷售價格，p2表示網絡渠道銷售價格。

s——決策變量，s1表示傳統渠道服務水平，s2表示網絡渠道服務水平。

c（s）=ηs2/2——服務成本函數，根據文獻[15]，當渠道的服務水平為s時所付出的成本為c（s），其中參數η表示服務的成本效率，η值越小，服務成本越有效。c0為產品的購貨成本。

a——某一產品的市場總需求。

r——傳統實體渠道的市場占比，總占比為1，則網絡渠道的市場占比為1-r，0〈r〈1。

k1——價格彈性系數，表示產品的價格變動對本渠道市場需求的影響。

k2——服務彈性系數，表示產品服務水平的變動對本渠道市場需求的影響。

e1——需求對價格的差異轉移系數，表示產品的價格變動引起的渠道間差距。

e2——需求對服務水平的差異轉移系數，表示產品的服務水平變動引起的渠道間差距。

1.2 相關函數確定

（1） 需求函數

基于Dan、Huang[16-18]等人構造的線性需求函數，兩個渠道的需求函數如下。

傳統渠道需求：

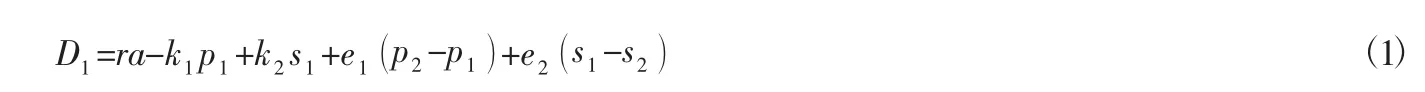
網絡渠道需求：

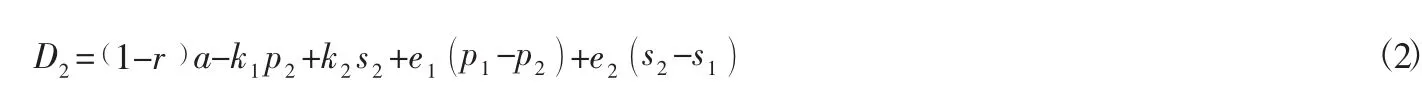
（2） 收益函數

線上和線下的收益都是由銷售收入減去各渠道的成本得到，零售商傳統渠道和網絡渠道的收益函數如下。

傳統渠道的收益：

網絡渠道的收益：

零售商總收益：

2 定價策略及推論

2.1 集中決策下考慮服務水平的定價策略

為避免內部競爭，零售商將實體渠道和網絡渠道作為一個整體統一決策，通過雙渠道內部的配合追求整體利益的最大化。此時整體收益函數πA為：

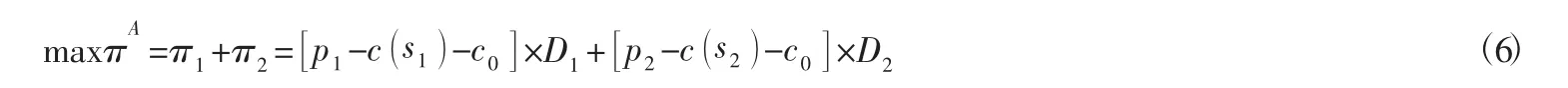
代入式 （1），式 （2） 得：

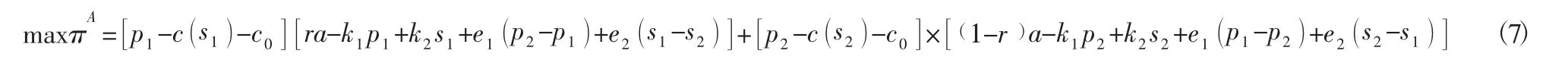
式（7）是集中決策下零售商的渠道利潤之和，給定s1、s2，則式（7）是關于價格變量的二元凹函數，由該收益函數最大值的一階偏導條件，可知p1,p2應滿足：

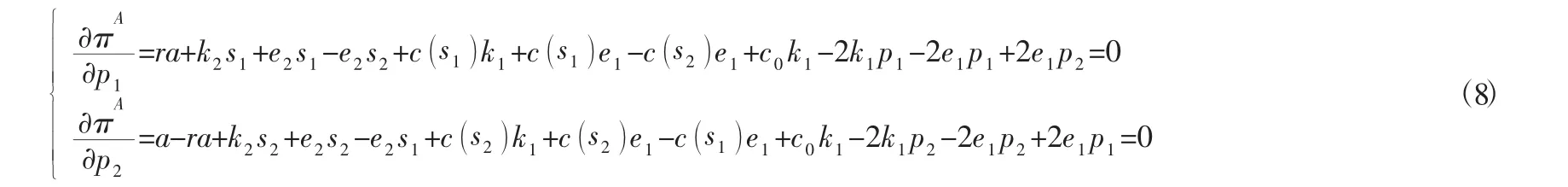
聯立求解，得出集中決策下，零售商線上線下的最優價格分別為：

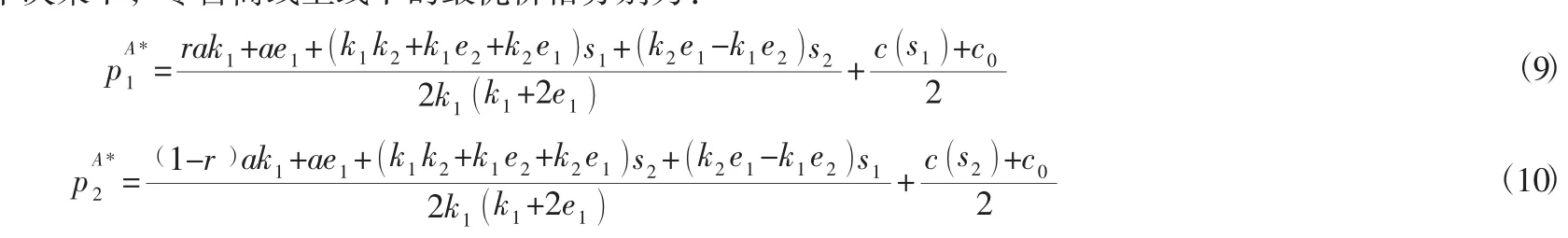
在最優定價的均衡解基礎上，提出以下推論：

推論1：雙渠道零售商的服務水平和提供該服務的渠道銷售價格成正相關關系。

推論2：服務水平對價格的影響和產品的消費者市場類型有關。

k2e1-k1e2的決定的正負，k2e1-k1e2的正負可用來比較，這兩個分式分別表示價格、服務對市場需求的影響。

推論3：集中決策下，網絡渠道服務水平變化對本渠道的影響大于對實體渠道的影響；同樣，實體渠道提供的服務對本渠道的影響大于對網絡渠道的影響。

2.2 分散決策下考慮服務水平的定價策略

兩個渠道分別相互獨立地進行決策時，實現各自利潤最大化，獨立地制定自己的定價策略，即式（3）和式（4）分別取最大值。本文對網絡渠道主導的情況進行討論，實體渠道主導同理。Stackelberg博弈有兩個階段，采用逆向歸納法求解。

具體描述如下：

首先，網絡渠道根據市場情況做出預估，給出定價p2，由多元函數的最大化一階條件可得下式，此時p2為給定，得到使得實體渠道利益最大化的最優價格：

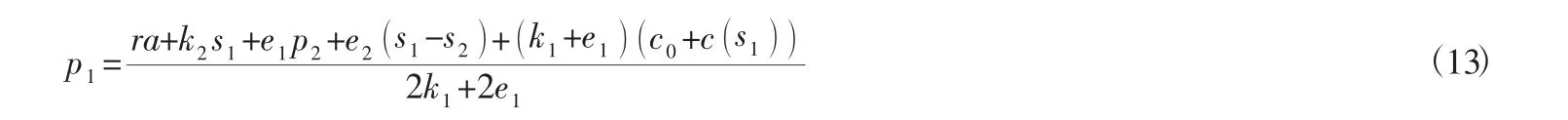
然后將計算得到p1代入網絡渠道的收益函數即將實體渠道的反應函數代入網絡渠道的模型定價，由求得使網絡渠道利益最大化的最優定價

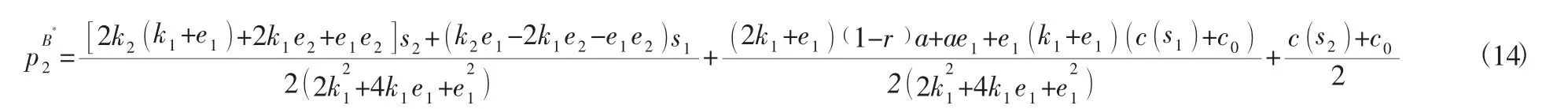
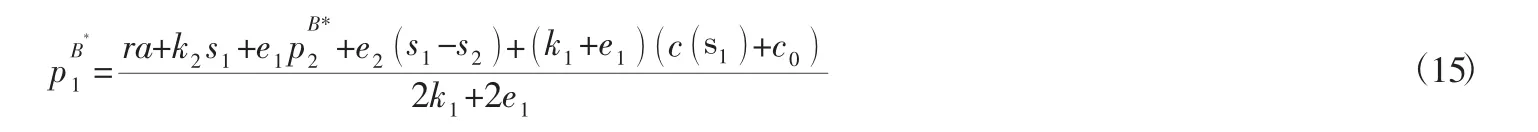
由此可得結論2：零售商雙渠道相互作用情況下，由網絡銷售渠道主導定價的Stackelberg博弈中，雙渠道零售商的最優定價策略）分別為：

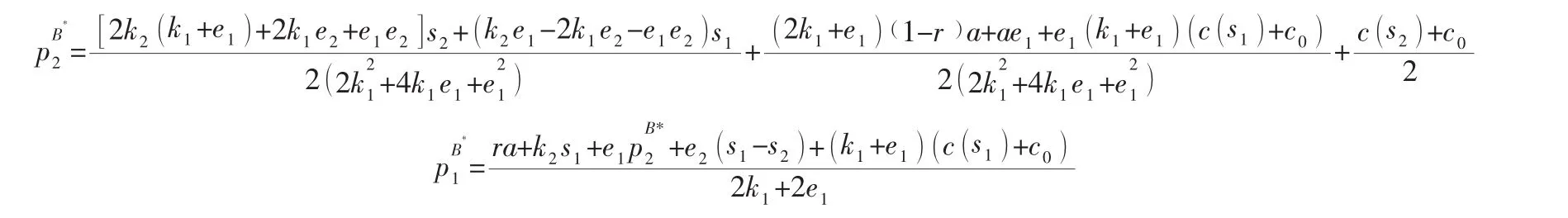
由差異化定價最優解的表達式可知，網絡渠道價格和本渠道服務、另一渠道服務水平都存在線性關系。基于此，得出以下推論：

推論4：分散決策情況下，雙渠道零售商的渠道服務水平和本渠道的銷售價格有正向線性關系。

證明：對分散決策情況的價格求服務的偏導如下：

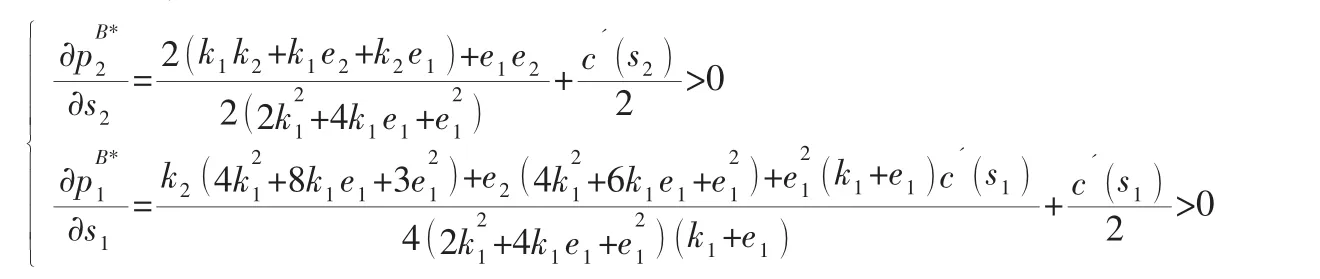
p1、p2分別隨s1、s2的增大而增大，此推論得證。

推論5：網絡渠道主導定價的分散決策下，服務水平影響價格存在臨界值。

設傳統渠道服務水平臨界值為α，網絡渠道服務水平臨界值為β。若傳統渠道服務水平低于α時，提高該渠道的服務，網絡渠道價格應隨之降低；若傳統渠道服務水平高于α時，提高線該渠道的服務，網絡渠道價格反而要隨之增加，降低消費者不同渠道比價的心理落差，以保護傳統渠道市場份額。β同理。

證明：由下式可知：

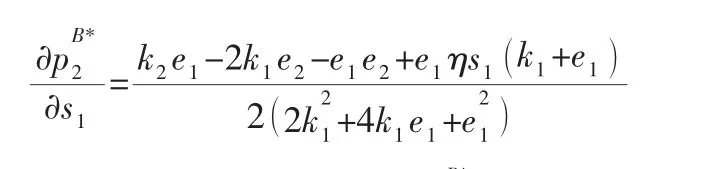
3 結論

本文在研究中，引入服務水平參數，利用博弈論對價格需求模型進行分析求解，研究實體渠道和網絡渠道的不同服務水平對零售商價格策略的作用機制。研究結果表明：（1）服務水平和渠道價格之間存在顯著的關系，零售商在選擇定價和服務策略時應該針對商品特性進行市場分類采取不同的定價策略。（2）不論是價格敏感或者是服務敏感的消費者，零售商提高服務水平應該控制在一個標準以內，防止因高質量服務引起高價而導致的顧客流失。（3）服務水平和市場中消費者需求的變化關系密切，零售商應隨時關注市場需求變化，根據臨界值調整服務和價格策略。